Навигация
Высказывания и булевы функции
116991
знак
7
таблиц
2
изображения
4.1.2 Высказывания и булевы функции
Одной из основных задач алгебры высказываний является установление значения истинности сложных высказываний в зависимости от значения истинности входящих в них простых высказываний. Для этого целесообразно рассматривать сложные высказывания как функции входящих в них простых высказываний. С другой стороны, так как значение истинности (и или л) сложного высказывания зависит по определению логических связок не от самих простых высказываний, а лишь от их значения истинности, то можно считать, что любое сложное высказывание определяет функцию, аргументы которой независимо друг от друга принимают значения и или л, а значение самой функции также принадлежит множеству {и, л} (конечно, существенно не то, что речь идет о функциях от нескольких аргументов из множества {и, л} в множество {и, л}, а лишь то, что данные множества двухэлементны. Эти множества зачастую обозначают не через {и, л}, а, например, через {0, 1}, считая, что 1 означает «истину», а 0 – «ложь»).
Такие функции называются булевыми функциями (по имени Д. Буля). Например, формула F (а, b, с) = (а Ù b) Þ (с Ù а) описывает, учитывая определение входящих в нее связок, булеву функцию, задаваемую следующей таблицей:
| а | b | с | F(a, b, с) | а | b | с | F(a, b, с) |
| и | и | и | и | л | и | и | и |
| и | и | л | л | л | и | л | и |
| и | л | и | и | л | л | и | и |
| и | л | л | и | л | л | л | и |
Заметим, что булевых функций от n аргументов имеется лишь конечное число, а именно столько, сколько возможно функциональных таблиц. Число возможных наборов аргументов равно 2n, а каждому набору аргументов можно независимо друг от друга сопоставлять одно из значений и или л. Таким образом, число всевозможных булевых функций от n аргументов равно 
– Оно очень быстро растет с ростом n. Изучение свойств булевых функций имеет большее значение как для алгебры и математической логики, так и для их приложений в кибернетике и теории автоматов. Естественно распространить определение высказывательных связок, так как мы их определили выше, на булевы функции. Мы ограничимся рассмотрением лишь связок Ù, Ú, ù называемых булевыми связками (или булевыми операциями). Такое ограничение оправдано тем, что, как легко проверить, связки Þ и Û могут быть выражены через другие булевы связки. При помощи таблиц истинности, приведенных выше, легко проверяются следующие тождества:
a Þ b º (ù a) Ú b;
a Û b º (a Ù b) Ú (ù a Ù ùb),
которые позволяют повсеместно заменить связки Þ, Û на Ù, Ú, ù.
Если мы теперь имеем булевы функции {F (xl, х2, ..., хn), G (х1, х2, ..., хn)} от n переменных, то действие связок над ними определяется естественным образом:
F (xl, x2, ..., хn) Ù G (х1, x2, ..., хn), F (xl, x2, ...,хn) Ú G (xl, x2, ..., хn), ùF (xl, x2, ..., хn) – это такие булевы функции, которые принимают значения, предписываемые соответствующими таблицами для каждого возможного значения аргументов. Кратко: булевы операции так переносятся на булевы функции, как действия арифметики переносятся на обычные функции числовых аргументов. Вообще имеет место далеко идущая аналогия между обычной алгеброй чисел и числовыми функциями, с одной стороны, и высказываниями и булевыми функциями – с другой. При этом можно отметить, что в одном определенном смысле алгебра булевых функций проще алгебры числовых функций: если рассматривать лишь функции некоторого конечного числа аргументов, то таких функций лишь конечное число. Поэтому выкладки с булевыми функциями вполне доступны пониманию школьников старших классов.
Естественно, закономерности булевой алгебры менее привычны и вызывают удивление и недоверие: это судьба всякого новшества.
Выпишем законы булевой алгебры. Большими латинскими буквами А, В, ..., X, Y, Z мы обозначим объекты, над которыми осуществляются булевы операции Ù, Ú, ù. Для определенности будем считать, что эти объекты – булевы функции некоторого фиксированного числа переменных. Среди них есть два особых элемента: 1, 0. Это соответственно функции, принимающие для всех аргументов значения 0 и 1 (постоянные функции – нуль и единица). Тогда
А Ù В = В Ù А, A Ú B = B Ú A
A Ù (В Ù C) = (А Ù В) Ù C A Ú (В Ú C) = (А Ú В) Ú C
A Ù A = A A Ú A = A
A Ù 1 = A A Ú 1 = A
A Ù 0 = 0 A Ú 0 = A
ù(A Ù B) = ùA Ú ùB ù(A Ú B) = ùA Ù ùB
A Ù (B Ú C) = (A Ù B) Ú (A Ù C) A Ú (B Ù C) = (A Ú B) Ù (A Ú C)
ù ùA = A
Если, как это обычно делают, булевы операции Ú, Ù, ù считать аналогом сложения, умножения и перехода к противоположному числу, то некоторые из вышеприведенных законов те же, что для числового сложения и умножения, другие же существенно отличаются от привычных.
Похожие работы
... neat as ninepence - чистенький, аккуратный; с иголочки; a twice-told tale - старая история, что-либо часто повторяемое и потому хорошо известное. 2. Значения числовых компонентов в английских фразеологических единицах Имена числительные, являясь абстрактным показателем количества однородных предметов, обозначением их счета, замкнуты в своеобразную категорию количественных слов, которые лишены ...
... схемы; 9) способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики, как геометрия, Сторонники шестого подхода считают, что математическое мышление является мышлением теоретическим и имеет такую же последовательность становления от эмпирического к аналитическому, к планирующему, рефлексирующему (Р. Атаханов, В.В. Давыдов, Ле Тхи Кхань Кхо, ...
... с активными познавательными обследовательскими действиями, со способностью к замещению предметов посредством условных знаков, символов».(7,с.126) 3. Моделирование в развитии математических представлений дошкольников Поиск эффективных средств познавательного развития детей, выявление условий становления познавательной деятельности в дошкольном детстве является темой научных работ многих ...
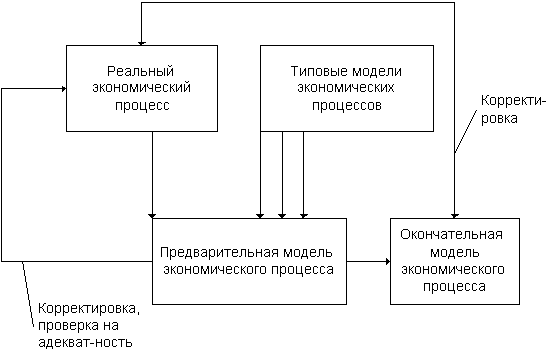
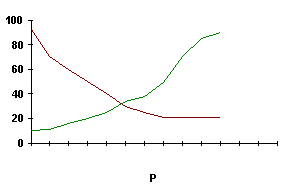
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...
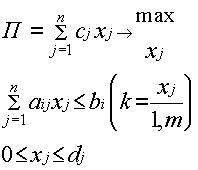
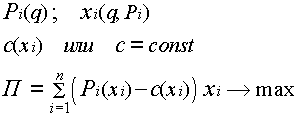
0 комментариев