Навигация
Символика Декарта и развитие алгебры
2.3 Символика Декарта и развитие алгебры.
В сочинении «Исчисление г. Декарта» неизвестный автор изложил арифметические основы математики Декарта. Они писал: «Эта новая арифметика состоит из букв a, b, c и т.д., а также из цифр 1, 2, 3 и т.д. Если цифры стоят перед буквами, например, 2а, 3b, 1/4с, то это означает, что величина а берется двойной, величина b – тройной, а от величины с берется четверть. Но если они находятся позади букв, например, а3, b4, c5, то это означает, что величина а умножается сама на себя три раза, величина b – четыре раза, а величина с – пять раз». «Сложение производится с помощью такого знака +. Так, чтобы сложить а и b, я пишу а + b. Вычитание производится с помощью такого знака –. Так, чтобы вычесть а из b, я пишу b – a и т. д. Если в вычитаемом выражении есть несколько частей, то у них в нем изменяются лишь знаки. Так, если из d требуется вычесть а – b + с, то останется d – а + b – –с. Точно так же при вычитании а2 – b2 из с2 – d2 останется с2 – d2 – а2 + b2. Но если имеются присоединенные цифры и члены одинакового вида, то их следует подписывать друг под другом и производить их сложение и вычитание как в обыкновенной арифметике... Если требуется умножить одну букву на другую, то их следует лишь соединить вместе, но если имеются присоединенные, числа, то они следуют законам обыкновенной арифметики. Что касается знаков, то известно, что + на + дает в произведении + и что –, умноженный на –, также дает в произведении +. Но + на – или же –, умноженный на +, дает в произведении –».
Точно так же определялись действие деления, операции с дробями «по правилам обыкновенной арифметики». Вот рассуждение о корне: «Когда корень извлечь из квадрата нельзя, его квадрат помещают под связку ![]() , чтобы отметить, что его следует рассматривать как корень, и тогда его корень называют иррациональной величиной».
, чтобы отметить, что его следует рассматривать как корень, и тогда его корень называют иррациональной величиной».
Из всего этого видно, как далеко зашла формализация алгебраических действий по сравнению с тем, что было у древних греков и у предшественников Декарта; видно также, что надобности в геометрической интерпретации алгебры уже нет.
Формализации алгебры (и всей математики) чрезвычайно способствовало то, что Декарт усовершенствовал буквенную символику. Он обозначал известные величины буквами а, b, с, . . ., неизвестные («неопределенные») – буквами x, y, z, .... Он ввел обозначения степеней: a2, a3 , х3 , . . . Правда, квадраты величин он выражал и с помощью символов аа, хх. Обозначение корня несколько отличается от современного. Так, выражение 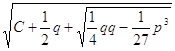 означает один из кубических корней, входящих в формулу Кардано.
означает один из кубических корней, входящих в формулу Кардано.
Все буквы в формулах Декарта считались положительными величинами; для обозначения отрицательных величин ставился знак минус; если знак коэффициента произволен, перед ним ставилось многоточие. Знак равенства имел необычный вид ![]() . Вот как, например, выглядело уравнение с произвольными коэффициентами:
. Вот как, например, выглядело уравнение с произвольными коэффициентами:
+x4…px3…qx…![]() 0.
0.
И еще один символ применял Декарт: он ставил звездочки, чтобы показать отсутствующие члены уравнения, например:
x5*** – b ![]() 0.
0.
Другие математики того времени тоже пользовались символикой, близкой к разработанной Декартом, а древние греки излагали свои мысли вообще без символики. Ферма построил аналитическую геометрию, располагая запасом употребляемых до него алгебраических средств. «...все это может побудить нас недооценить те успехи, которые поставлены здесь во главу всей математической деятельности Декарта. Значение этих успехов становится, однако, понятным, если мы примем во внимание, как часто мы должны были для изложения идей более ранних авторов прибегать к пользованию алгебраической формой Декарта; без нее мы вряд ли смогли бы это сделать сколь-нибудь сжато и наглядно. Мы смогли воспользоваться этой алгебраической формой, с одной стороны, потому что декартова трактовка алгебры благодаря своим преимуществам получила ныне широкое распространение, и знакомство с ней происходит уже в школе. С другой стороны, она уже сама по себе в большой мере расчистила путь многому, что раньше могло быть изложено лишь весьма громоздким образом и было поэтому доступно лишь очень способным математикам» (Цейтен Г. Г, История математики в XVI и XVII веках, с. 202)
Иными словами, разработка и введение алгебраической символики сделали математику более демократичной.
Уравнения, по утверждению Декарта, представляют собой равные друг другу суммы известных и неизвестных членов или же, если рассматривать эти суммы вместе, равны «ничему» (нулю). Декарт указал, что «уравнения часто удобно рассматривать именно последним образом», т. е. в виде Р (х) = 0. Для теоретических построений Декарта такая запись уравнений играла важную роль.
Этой формой он пользовался при установлении числа корней алгебраического уравнения, что привело к формулировке основной теоремы алгебры: число корней уравнения (положительных - «истинных», отрицательных - «ложных» и мнимых - «воображаемых») равно числу единиц в наивысшем показателе степени входящей в уравнение неизвестной величины. Справедливость теоремы он аргументировал тем, что при перемножении n двучленов вида х – а получается многочлен степени n. Недостающие «воображаемые» корни, природу которых Декарт не разъясняет, можно примыслить.
Если все корни положительны, то, по словам Декарта, дело обстоит так: «Знайте, что всякое уравнение может иметь столько же различных корней или же значений неизвестной величины, сколько последняя имеет измерений; ибо если, например, принять х равным 2, или же х – 2 равным ничему, а также х = 3 или же х – 3 = 0, то, перемножив оба эти уравнения x – 2 = 0 и x – 3 = 0, мы получим хх – 5х + 6 = 0, или же хх = 5x – 6, уравнение, в котором величина х имеет значение 2 и вместе с тем значение 3.
Если принять еще, что х – 4 = 0 и умножить это выражение на хх – 5x + 6 = 0, то мы получим х3 – 9хх + 2бх – 24 = 0, другое уравнение, в котором х, обладая тремя измерениями, имеет вместе с тем три значения, а именно 2, 3 и 4»
Если же «х выражает собой также недостаток какой-нибудь величины, скажем 5, то мы получим х + 5 = 0». Умножив х + 5 на левую часть предыдущего уравнения и приравняв результат нулю, получим
x4 – 4x3 – 19xx + 10бх – 120 = 0, (1)
«уравнение, у которого четыре корня, именно три истинных 2, 3, 4 и один ложный –5».
Построение левой части уравнения в виде произведения двучленов приводит к тому, что степень уравнения можно понизить, разделив левую часть его на х – a, где а – корень уравнения. С другой стороны, если такое деление невозможно, то число а не будет корнем уравнения. Левую часть уравнения (1), например, можно разделить на х – 2, х – 3, х – 4, х + 5 и нельзя разделить на любой другой двучлен х – а; «это показывает, что оно может иметь лишь четыре корня: 2, 3, 4 и –5».
Декарт сформулировал правило знаков, дающее возможность установить число положительных и отрицательных корней уравнения: «Истинных корней может быть столько, сколько раз в нем изменяются знаки + и –, а ложных столько, сколько раз встречаются подряд два знака + или два знака –». Впоследствии он внес уточнение: при наличии мнимых («невозможных») корней уравнения число положительных корней может (а не должно) быть равным числу перемен знаков. Декарт высказал правила и на примерах показал, какие следует выполнять преобразования, чтобы изменить знаки корней уравнения, увеличить или уменьшить корни, получить уравнение, не содержащее второго члена, и т. д. «Легко, далее, сделать так, чтобы все корни одного и того же уравнения, бывшие ложными, стали истинными, и вместе с тем все бывшие истинными стали ложными; именно это можно сделать, изменив на обратные все знаки + или –, стоящие на втором, четвертом, шестом и других, обозначенных четными местах, не изменяя знаки первого, третьего, пятого и им подобных, обозначенных нечетными числами мест».
Применив такое преобразование к уравнению (1), получим уравнение
х4 + 4x3 - 19хх – 106x - 120 = 0, (2)
имеющее один положительный корень 5 и три отрицательных: –2, –3, –4.
Можно, не зная корней уравнения, увеличить или уменьшить их на какую-либо величину, для чего необходимо сделать соответствующую замену. Например, уравнение (2) после замены х = у – 3 преобразуется к виду y3 – 8у2 – у + 8 == 0; его положительный корень 8 превышает положительный корень уравнения (2) на 3.
Декарт заметил, что, «увеличивая истинные корни, мы уменьшаем ложные и наоборот», при этом он имел в виду абсолютные величины корней.
Правило исключения второго члена уравнения, известное еще Виету, Декарт иллюстрировал примерами.
Так, уравнение y4+ 16y3 + 71y2 – 4y –120 = 0 подстановкой z – 4 = у он сводил к
z4 – 25z2 – 60z – 36 = 0; его корни –3, -2, -1, 6.
Второй член уравнения x4 - 2ах3 + х2 (2а2 - с2) - 2aзx + а4 = 0 он исключал подстановкой х = z + ![]() a его к виду z4 + z2 (
a его к виду z4 + z2 (![]() a2 – c2) – z (a3 + ac2) +
a2 – c2) – z (a3 + ac2) + ![]() a4 –
a4 – ![]() a2c2 = 0.
a2c2 = 0.
Декарт говорил, что можно также «сделать, чтобы все ложные корни уравнения стали истинными, но истинные не стали ложными». Он утверждал, что легко приблизительно оценить величину неизвестных отрицательных корней уравнения. В этом можно усмотреть постановку вопроса о границах действительных корней уравнения, которому впоследствии уделил большое внимание Ньютон.
Для умножения и деления неизвестных корней уравнения на число, приведения дробных и иррациональных коэффициентов к целым Декарт пользовался теми же подстановками, которые были известны и Виету. Рассмотрим пример.
Если положить у = х![]() и z = 3у, то уравнение
и z = 3у, то уравнение
x3 – x2![]() +
+ ![]() x –
x – ![]() = 0
= 0
преобразуется последовательно в уравнение
y3 – 3y2 + ![]() y –
y – ![]() = 0, а затем в z3 – 9z2 + 26z – 24 = 0.
= 0, а затем в z3 – 9z2 + 26z – 24 = 0.
Корни окончательного уравнения 2, 3, 4; предыдущего – ![]() , 1,
, 1, ![]() ; первого –
; первого – ![]()
![]() ,
, ![]()
![]() ,
, ![]() .
.
О «воображаемых» (мнимых) корнях уравнения Декарт писал: «Как истинные, так и ложные корни не всегда бывают действительными, оказываясь иногда лишь воображаемыми. Другими словами, хотя всегда можно вообразить себе у каждого уравнения столько корней, сколько я сказал, но иногда не существует ни одной величины, которая соответствует этим воображаемым корням. Так, например, хотя у уравнения х3 – 6xx + 13x –10 = 0 можно вообразить себе три корня, но на самом деле оно имеет только один действительный, именно 2. Что касается двух других корней, то сколько бы их ни увеличивать, уменьшать или умножать так, как я только что объяснил, все равно их не удастся сделать иными, чем воображаемыми».
Еще одна чрезвычайно важная задача алгебры была поставлена Декартом – задача приводимости уравнений, т. е. представления целого многочлена с рациональными (целыми) коэффициентами в виде произведения многочленов низших степеней. Декарт установил, что корни уравнения третьей степени с целыми коэффициентами и старшим коэффициентом, равным единице, строятся с помощью циркуля и линейки (иначе говоря, уравнение разрешимо в квадратных радикалах) тогда и только тогда, когда уравнение имеет целый корень (т. е. левая часть его может быть представлена в виде произведения множителей первой и второй степеней).
Для уравнения четвертой степени он также указал условие разрешимости; оно состоит в разрешимости его кубической резольвенты, т. е. соответствующего уравнения шестой степени, кубического относительно у2.
Декарт не показал, как он получил окончательный результат. Ф. Схоотен вывел резольвенту с помощью метода неопределенных коэффициентов. Он представил многочлен четвертой степени в виде x4 – px2 – qx + r = (x2 + yx + z)(x2 – yx +v), откуда получил уравнения для нахождения у, z, у: z – y2 + v = –p, –zy+vy = –q, vz = r.
Разрешающее уравнение (резольвента) имеет вид у6 – 2ру4 + (р2 – 4г)y2 – q2 = 0.
В конце третьей книги «Геометрии» Декарт графически решал уравнения третьей, четвертой, пятой и шестой степеней, отыскивая их корни как пересечение некоторых линий.
Вклад Декарта в математику не ограничивается одной «Геометрией»: в его переписке содержатся решения многих задач, в том числе связанных с бесконечно малыми.
§3 Обозначение производной и интеграла у Лейбница и развитие анализа.
Лейбниц внес большой вклад в развитие математического анализа. Ему принадлежит создание многих символов, которые мы используем сейчас, например, dx, ddx,…, d2x, d3x, ![]() ,
, ![]() . Но символы эти появились у Лейбница не сразу. Первоначально выражение
. Но символы эти появились у Лейбница не сразу. Первоначально выражение ![]() = хu
= хu![]() (1)
(1)
у него выглядело следующим образом: omn. xw = ult. х×omn. w – omn. omn. w. При этом он еще не употреблял привычного нам знака равенства.
В этом выражении omn. – начальные буквы латинского слова omnia, т. е. все, – обозначает объединение, суммирование «всех» бесконечно малых элементов, стоящих под этим знаком, х обозначает абсциссу точки на кривой, исходящей из начала координат, w в этих выкладках Лейбница обозначает то элемент дуги (ds), то дифференциал ординаты (dy), ult. – начальные буквы латинского слова ultima (т. е. последняя) – относится к абсциссе.
Для Лейбница в данном случае его omn.w выступает в роли новой функции, которая сама становится объектом операции, обозначенной omn. Как это обстоятельство, так и то, что он рассматривает результат многократного применения преобразования вида (1) и получает выражения, в которых операция omn. наслаивается несколько раз, заставило его искать более удобное обозначение, и в записи от 29 октября мы читаем: полезно писать ![]() вместо omn., так что
вместо omn., так что ![]() будет вместо omn.
будет вместо omn.![]() (
(![]() - это начальная буква слова summa и Лейбниц называет этот знак суммой). И для нового исчисления, как в той же записи выражается Лейбниц, имеем
- это начальная буква слова summa и Лейбниц называет этот знак суммой). И для нового исчисления, как в той же записи выражается Лейбниц, имеем
![]() ,
, ![]() ,
, ![]() =
=![]() ,
, ![]() .
.
Первое из этих соотношений соответствует преобразованию (1), а, b - постоянные, черта сверху играет роль скобки, и она, собственно, лишняя, да и Лейбниц не всегда ее пишет, но ее, пусть несистематическое, появление характерно: так, в записи х![]() мы видим, что пишущему кажется необходимым дополнительно указать, что на х действительно умножаются все
мы видим, что пишущему кажется необходимым дополнительно указать, что на х действительно умножаются все ![]() , собранные в сумму знаком
, собранные в сумму знаком ![]() . Лейбниц далее записывает (по поводу формул (2) и их вариантов): «Это достаточно ново и примечательно, поскольку указывает на новый вид исчисления», и переходит к обратному исчислению (contrario calculo), вводя символ d, который «уменьшает измерение так, как увеличивает
. Лейбниц далее записывает (по поводу формул (2) и их вариантов): «Это достаточно ново и примечательно, поскольку указывает на новый вид исчисления», и переходит к обратному исчислению (contrario calculo), вводя символ d, который «уменьшает измерение так, как увеличивает ![]() », но пишет его в знаменателе (не dy, a y/d).
», но пишет его в знаменателе (не dy, a y/d).
Тут же читаем: ![]() обозначает сумму, d - разность. Несколькими днями позже, в рукописи, помеченной 10 ноября, Лейбниц записывает: «dx — то же самое, что x/d, то есть разность между двумя ближайшими».
обозначает сумму, d - разность. Несколькими днями позже, в рукописи, помеченной 10 ноября, Лейбниц записывает: «dx — то же самое, что x/d, то есть разность между двумя ближайшими».
Замечательно то, что Лейбниц сразу, введя новое обозначение, начинает с ним обращаться как с символом операции, отделяя его от объекта операций: он сразу отметил, что его «сумма» от (двух) слагаемых равна сумме «сумм» слагаемых и что постоянный множитель или делитель можно выносить за знак «суммы». В записях последующих дней (от 1, 10, 11 ноября) он отмечает такие же свойства операции, обозначенной через d. За эти дни Лейбниц убедился, что d(xy) не то же самое, что dx×dy, и что d(x/y) ¹ dx/dy, но не вывел еще соответствующих формул. Отметил он и что ![]() , конечно, не то же самое, что
, конечно, не то же самое, что ![]() . Он уже систематически использует обратность действий
. Он уже систематически использует обратность действий ![]() и d, например, после равенства
и d, например, после равенства ![]() он пишет: или wz = y2/2d (тут d еще в знаменателе). Отмечены им уже формулы для производной степенной функции при целых показателях степени, например, «из квадратуры треугольника ясно, что y2/2d = у;
он пишет: или wz = y2/2d (тут d еще в знаменателе). Отмечены им уже формулы для производной степенной функции при целых показателях степени, например, «из квадратуры треугольника ясно, что y2/2d = у; ![]() =
= ![]() из квадратуры параболы».
из квадратуры параболы».
А в том, что он открывает здесь нечто весьма существенное, Лейбниц, вероятно, окончательно убедился, когда смог использовать пока как бы нащупываемый им алгоритм при решении задач на обратный метод касательных. Он писал: «Еще в прошлом году я поставил перед собой вопрос, который можно отнести к труднейшим во всей геометрии, поскольку распространенные до сих пор методы здесь почти ничего не дают. Сегодня я нашел его решение и я приведу его анализ».
Свою задачу Лейбниц формулирует как определение кривой, у которой поднормали обратно пропорциональны ординатам. Такая задача сводится, в современных обозначениях, к решению дифференциального уравнения ydy/dx = k/y, где k - постоянная. Решение Лейбница состоит по сути в составлении такого уравнения и последующем его интегрировании с помощью разделения переменных. Он получил, таким образом, уравнение искомой кривой, и она оказалась кубической параболой.
По записям Лейбница видно, что к середине 1676 г. он, располагая уже всеми основными правилами дифференцирования и интегрирования, решил еще несколько задач на обратный метод касательных, в том числе знаменитую в XVII в. задачу де Бона, предложенную в свое время Декарту, который не смог получить ее общее решение. И это результат вполне самостоятельного хода мыслей. То, что Лейбниц знал к тому времени относительно результатов Ньютона и Грегори, никак не могло помочь ему пройти избранный им путь. Операционный подход Лейбница к проблеме и его поиски рациональной символики для нового исчисления, в чем наиболее полно выразилась творческая индивидуальность Лейбница, были в достаточной мере чужды его английским соперникам.
Примерно через год после открытий 1675 г., во время поездки по Голландии и после встречи там с Гудде, Лейбниц составил заметку, озаглавленную «Дифференциальное исчисление касательных». Она начинается записями:
d![]() = 1, d
= 1, d![]() = 2x, d
= 2x, d![]() = Зх2 и т. д.
= Зх2 и т. д.
d![]() = –
= –![]() , d
, d![]() = –
= –![]() , d
, d![]() = –
= – ![]() и т. д.
и т. д.
d![]() =
=![]() и т. д.
и т. д.
Отсюда выводится общее правило для разностей и сумм простых степеней:
d![]() = exe-1 и, напротив,
= exe-1 и, напротив, ![]() =
=![]() (горизонтальная черта сверху означает взятие в скобки).
(горизонтальная черта сверху означает взятие в скобки).
Как видно, здесь знак d обозначает операцию вычисления производной. Но Лейбниц еще не вполне выработал к тому времени свою символику и чуть ниже можно прочитать, что «общее правило устанавливается так: ![]() и, наоборот,
и, наоборот, ![]() ». Такая редакция общего правила следует за замечанием: «пусть у = x2, тогда будет
». Такая редакция общего правила следует за замечанием: «пусть у = x2, тогда будет ![]() = 2x
= 2x![]() , следовательно,
, следовательно, ![]() = 2x». И на полях, вероятно, позже, Лейбниц написал, что это отличное замечание к его исчислению разностей: «если by
= 2x». И на полях, вероятно, позже, Лейбниц написал, что это отличное замечание к его исчислению разностей: «если by![]() +
+ ![]() + etc. = 0, то b
+ etc. = 0, то b![]() +
+![]() = 0, и так с остальными». Здесь он начинает свободно обращаться с дифференциалами, как это ему удобно при решении дифференциальных уравнений, не предопределяя, какое из переменных независимое, какое функция.
= 0, и так с остальными». Здесь он начинает свободно обращаться с дифференциалами, как это ему удобно при решении дифференциальных уравнений, не предопределяя, какое из переменных независимое, какое функция.
Дальше в том же наброске следует замечание, что вот, «возьмем какое-либо уравнение (но берется уравнение алгебраической кривой, притом второго порядка) ... и напишем у +dy вместо у и подобным образом x + dx вместо х, тогда, опустив то, что опустить надлежит, получим другое уравнение» (т. е. оставляются только слагаемые первого порядка относительно дифференциалов, и это показано на примере).
Отсюда вытекает правило, обнародованное Слюзом, продолжает Лейбниц, и это, конечно, верно. Тут же он добавляет, что «мы бесконечно расширим это правило: пусть букв будет сколько угодно и из них составлена формула, например, из трех букв...». И Лейбниц сопоставляет уравнение алгебраической поверхности опять-таки второго порядка и небезупречно составленное путем дифференцирования соотношение между дифференциалами, чтобы заявить без дополнительного обоснования: «Отсюда явствует, что по такому методу получаем касательные плоскости поверхностей, и не имеет значения при этом, существует ли еще иное соотношение между теми же буквами х, у, z, его ведь можно будет подставить позже».
Конечно, указание на то, как определить касательную плоскость к поверхности, следовало еще развить, что в рассматриваемом отрывке отсутствует, но мы видим здесь пример того, как Лейбниц постепенно, по разным поводам, возвращается к своему исчислению, расширяет область его применения, наряду с новыми результатами получает с его помощью известные старые.
В 1678 г. Чирнгаус заявил Лейбницу, что надо по возможности избегать новых обозначений, ибо это только затрудняет доступ к науке. Вот Виет заслуживает похвалы за то, что обходится буквенными обозначениями, не вводя новых чудовищных знаков. Лейбниц, возражая подчеркивал, что надо искать обозначения, которые кратко выражают сокровенную сущность предмета, облегчая путь к открытиям и значительно уменьшая затрату умственного труда. И таковы, продолжал Лейбниц, использованные мною знаки – я часто с их помощью в несколько строк решаю самые трудные задачи.
В 1684 г. в «Лейпцигских ученых заметках» появилась одна из самых знаменитых математических работ: «Новый метод максимумов и минимумов, а также касательных, для которого не являются препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления». В этой небольшой статье даны основы дифференциального исчисления. Правила дифференцирования приводятся без доказательств, хотя есть указания на то, что здесь все можно обосновать, рассматривая дифференциалы как бесконечно малые разности. Определение дифференциала функции дано как произведение производной (но производная задается геометрически как отношение ординаты к подкасательной) на дифференциал аргумента. Последний можно задавать произвольно. Еще не вводится определенное соглашение относительно выбора знака для длин отрезков, которыми оперирует Лейбниц, поэтому он привод некоторые формулы с двумя знаками. В статье были опечатки, затруднявшие чтение, были и ошибочные утверждения (относительно определения точек перегиба). Но в ней были и эффективные примеры применения нового алгоритма, и автор, приведя их, имел право заявить: «Во всех таких и много более сложных случаях наш метод обладает одной и той же поразительной и прямо беспримерной легкостью. Но это лишь начала некой более высокой Геометрии, которая распространяется на труднейшие и прекраснейшие задачи прикладной математики, и едва ли кому-нибудь удастся заняться с той же легкостью такими вещами, не пользуясь нашим дифференциальным исчислением или ему подобным».
Год 1690-й отмечает новый этап: начинается переписка и многолетнее научное общение Лейбница с Яковом Бернулли, а затем и его младшим братом Иоганном, напечатана первая работа по анализу старшего из братьев, и оба они, математики первого ранга, отныне все усилия приложат для развития нового исчисления.
Через посредство И. Бернулли с новым исчислением знакомится и становится его приверженцем самый значительный французский механик тех лет П. Вариньон.
На Лейбница появление приверженцев его метода и умножение примеров, показывающих плодотворность созданного им исчисления, действовало стимулирующе.
Новые результаты Лейбница достаточно разнообразны. Некоторые из них относятся к технике дифференцирования. Так, в «Новом методе...» 1684 г. дифференцируются только алгебраические функции, рациональные и иррациональные, и, в неявном виде, логарифм, а в 90-е годы Лейбниц, можно сказать, мимоходом в различных работах указывает дифференциалы синуса и арксинуса, функции вида uv, где основание и показатель степени — функции независимого переменного, вводит дифференцирование по параметру. Позже Лейбниц дает носящую его имя формулу для дифференциала любого порядка от произведения функций. Можно сказать, что на этой стадии операция дифференцирования у Лейбница охватила весь запас известных тогда функций.
Другая группа результатов Лейбница относится к дифференциальной геометрии. Один из наиболее существенных – введение огибающей семейства плоских кривых, зависящих от некоторого параметра.
В третью группу можно объединить результаты по интегральному исчислению. Кроме формул, представляющих собой обращение упомянутых формул дифференцирования, Лейбниц дал две работы об интегрировании рациональных дробей (1701 и 1703 гг.). В первой из них он допустил ошибку, сделав вывод, что при наличии комплексных корней у знаменателя рациональной дроби с действительными коэффициентами интегрирование должно ввести новые трансцендентные функции, кроме обратных круговых и логарифмов. Когда же И. Бернулли указал правильный результат, Лейбниц с ним не согласился и повторил свое ошибочное заключение во второй работе. Эта ошибка Лейбница – не только математический недосмотр, она имеет любопытные корни. Утверждение, что интегралы вида
![]() ,
, ![]()
дают новые трансцендентные функции казалось ему и привлекательным и правдоподобным еще потому, что это соответствовало лейбницевой метафизике. Если бы все интегралы такого вида сводились, как выражается Лейбниц, только к квадратуре гиперболы (т. е. логарифмам) и к квадратуре круга (к обратным круговым функциям), то все было бы единообразно. «Но природа, мать вечного разнообразия, или, лучше сказать, божественный дух слишком цепко оберегает свою прекрасную многоликость, чтобы допустить слияние всего в одну породу. И таким образом он находит изящный и удивительный выход в этом чуде анализа, этом побочном порождении мира идей, двойственном существе как бы между бытием и небытием, что мы называем мнимым корнем. И посему всякий раз, когда знаменатель рациональной дроби имеет мнимые корни, что может получиться бесконечно многими способами, будет мнимой и гипербола, квадратура которой нам нужна, и ее никоим образом нельзя будет построить».
От Лейбница не ускользнуло и то, что интеграл можно рассматривать как дифференциал с показателем –1, и это привело его к введению дифференциалов любых отрицательных и дробных порядков с помощью бесконечных рядов. Теорию интегралов и производных дробного порядка развивали в XVIII в. Эйлер, в XIX в. – Лиувилъ, Риман, Летников, в XX в. – Г. Вейль, М. Рис и др., и сейчас она составляет один из разделов анализа. Лейбниц же первый в печати указал на то, что операция интегрирования вводит произвольную постоянную и на связь между определением первообразной функции и квадратурой. Он указал также, как интегрировать некоторые типы обыкновенных дифференциальных уравнений. Существенно то, что Лейбниц отчетливо определил взаимоотношение интегрирования дифференциальных уравнений и интегрирования функций (первое следует считать выполненным, если оно сведено ко второму), и, аналогично, интегрирования функций и алгебраических операций (например, определение корней знаменателя подынтегральной рациональной дроби считается при интегрировании задачей решенной).
Лейбниц много занимался также интегрированием иррациональностей (в конечном виде, как стали позже выражаться) и глубоко проник в суть этой проблемы.
Заслугой Лейбница является и применение к интегрированию и функций и дифференциальных уравнений бесконечных рядов с использованием метода неопределенных коэффициентов (последний метод восходит к Декарту). Немалое значение для успехов нового анализа имело достаточно общее введение такого понятия, как функция, и систематические выступления Лейбница против ограничения (по Декарту) предмета геометрии изучением алгебраических кривых. Наконец, Лейбниц на деле доказал достоинства своего исчисления, с успехом участвуя в конкурсах на решение таких трудных для того времени задач, как задача Галилея о цепной линии и задача И. Бернулли о брахистрохроне.
Историческое значение математического творчества Лейбница огромно. Оно длилось около сорока лет, и за такой сравнительно небольшой срок математика преобразилась. Наука, в которую вступил Лейбниц, и наука, которую он оставил, принадлежит разным эпохам, и это плод главным образом его трудов и трудов его школы. До Лейбница в обширную область неведомого пытались проникнуть то тут, то там, наскоками, пусть порою очень удачными, не имея общего плана. Благодаря Лейбницу разрозненные прежде усилия были подчинены общей программе, прояснились и близкие и далекие цели, средства для их достижения оказались в распоряжении не только сверходаренных одиночек и значительно выиграли в эффективности.
§ 4. Язык кванторов и основания математической логики.
В связи с тем, что элементы логики представляют собой неотъемлемую составную часть школьного обучения математике, они должны изучаться в единстве с собственно математическим материалом на всех этапах обучения. Соответствующий язык необходимо вводить постепенно для обозначения уже разъясненных математических и логических понятий, чтобы в дальнейшем он становился необходимым компонентом обиходного математического языка.
Похожие работы
... neat as ninepence - чистенький, аккуратный; с иголочки; a twice-told tale - старая история, что-либо часто повторяемое и потому хорошо известное. 2. Значения числовых компонентов в английских фразеологических единицах Имена числительные, являясь абстрактным показателем количества однородных предметов, обозначением их счета, замкнуты в своеобразную категорию количественных слов, которые лишены ...
... схемы; 9) способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики, как геометрия, Сторонники шестого подхода считают, что математическое мышление является мышлением теоретическим и имеет такую же последовательность становления от эмпирического к аналитическому, к планирующему, рефлексирующему (Р. Атаханов, В.В. Давыдов, Ле Тхи Кхань Кхо, ...
... с активными познавательными обследовательскими действиями, со способностью к замещению предметов посредством условных знаков, символов».(7,с.126) 3. Моделирование в развитии математических представлений дошкольников Поиск эффективных средств познавательного развития детей, выявление условий становления познавательной деятельности в дошкольном детстве является темой научных работ многих ...
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...
0 комментариев