Навигация
Внутренние функции на комплексных полугруппах Ли над группой SU(p,q)
7887
знаков
0
таблиц
3
изображения
Д.А. Ланин, Омский государственный университет, кафедра математического анализа
Пусть 
- вещественная алгебра Ли, G - группа Ли с алгеброй . Выпуклый замкнутый острый телесный конус 
в алгебре , инвариантный относительно действия группы 
, будем называть инвариантным конусом. Среди всех таких конусов есть минимальный. Если - инвариантный конус, то множество 
оказывается замкнутой комплексной полугруппой (см. [1,2]) и называется полугруппой Ольшанского. Будем рассматривать группу G, алгебру и полугруппу Ольшанского в матричной реализации. Под внутренней функцией на полугруппе Ольшанского будем понимать голоморфную ограниченную рациональную (от матричных элементов) функцию без особенностей на границе, равную по модулю единице на группе G. Степень рациональной внутренней функции определим как максимум степеней числителя и знаменателя. Наша задача состоит в нахождении свойств внутренних функций на полугруппах Ольшанского над группой SU(p,q). Сходные вопросы рассматриваются в работах [3,4]. В [3] дано полное описание рациональных внутренних функций на поликруге. Этот результат распространен на произвольные ограниченные симметрические области в [4].
Через 
обозначим инволюцию, выделяющую группу 
в группе 
.
В настоящей работе получены следующие результаты:
Теорема 1. Каждая рациональная внутренняя функция на полугруппе л имеет вид 
где f(X) - многочлен от элементов матрицы X, а |C|=1.
Теорема 2. В случае минимального конуса степень рациональной внутренней функции на полугруппе Ольшанского над группой SU(p,q) не меньше, чем 
, причем эта оценка точная.
1. Основные понятия и обозначения
1.1. Говоря о блочной матрице 
, будем подразумевать, что A имеет размеры 
, а D - 
. Пусть 
, где 
. Тогда
Положим 
, т.е. - инволюция, выделяющая группу в группе . Если f(A) - многочлен от матричных элементов 
, то 
также будет многочленом от .
1.2. Поскольку 
- инвариантный, 
можно представить в виде
Поэтому, 
.
1.3. Пусть известно, что значения двух многочленов F(A) и H(A) от элементов матрицы A совпадают при 
. Эти многочлены не обязательно равны, и мы будем называть их эквивалентными. Класс эквивалентности, в котором лежит многочлен P, будем обозначать [P].
Определение. Будем говорить, что [P] и [Q] взаимно просты, если для любых 
и 
многочлены 
и 
не имеют общих нетривиальных (
) множителей.
Определение. Степенью рациональной функции 
будем называть 
, где 
, причем [P1] и [Q1] - взаимно просты, а P1 и Q1 имеют минимальную степень.
Корректность последнего определения гарантируется следующим фактом ([5]):
Теорема 3. В кольце многочленов на односвязной полупростой алгебраической группе разложение на простые множители однозначно.
Похожие работы
... компонентами группы . наличие в групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия. 1.3.1 Теорема. Пусть --- алгебраическая группа матриц. Её компонента , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы по (в частности, они являются связными компонентами ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... и в том случае, когда интегральный оператор (3) действует в пространстве C(W) и неразложим в этом пространстве относительно конуса неотрицательных функций пространства C(W). Получению оценок спектрального радиуса положительного оператора по информации о поведении этого оператора на фиксированном ненулевом элементе конуса посвящена достаточно обширная литература [21], [11], [13], [18], [26], ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
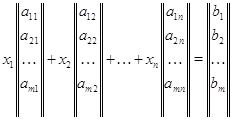
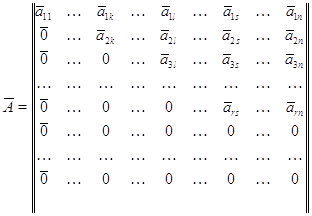
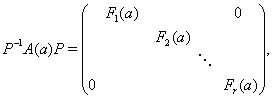
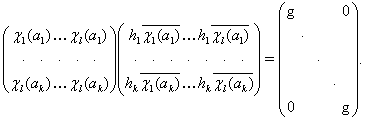
0 комментариев