Навигация
3. Доказательство теоремы 2
Пусть G=SU(p,q), 
=su(p,q) , 
- е" подалгебра Картана, 
- минимальный инвариантный конус. Тогда:
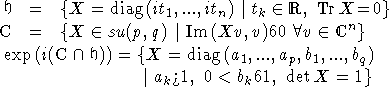
Пусть 
- внутренняя функция, такая, что степени многочленов P и Q минимальны.
1) Если 
, то положим
Заметим, что функция F принимает значение ноль в какой-то точке единичного круга 
. Действительно, если предположить противное, то функция 
будет аналитической в , в частности 
в (по принципу максимума модуля). С другой стороны, 
. Поэтому |F|=1, что противоречит многомерному принципу максимума модуля, поскольку ограниченная функция 
не может принимать значение, равное по модулю единице, во внутренней точке полугруппы л (рассматриваемой как область в 
).
Заметим также, что внутренним автоморфизмом можно непрерывно перевести Ak1l1(z) в Ak2l2(z), а, значит, и A(z) в B(z). Далее, поскольку интеграл
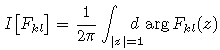
есть целое число (равное числу нулей функции Fkl, ввиду ее аналитичности), и подынтегральная функция меняется непрерывно при переходе от матрицы Ak1l1(z) к Ak2l2(z), получаем, что этот интеграл имеет одно и то же значение для любых k и l. Точно так же будут совпадать интегралы 
и 
. Если 
, то 
, т.к. B(z)=A11(zq).
Поскольку функция F имеет ноль внутри единичного круга, 
. Значит, рациональная функция F имеет по крайней мере q нулей в . А это говорит о том, что степень многочлена P, стоящего в числителе 
, не меньше, чем q.
2) Если p>q, то оценим степень через степень многочлена Q. Имеем: 
(см. (1.2)). Положив
и повторив вышеприведенные рассуждения с учетом того, что 
, получим следующую оценку: 
. Таким образом, 
. Докажем теперь, что указанная оценка достигается.
Предложение. Пусть 
. Тогда функция 
имеющая степень p, является внутренней на полугруппе Ольшанского над группой SU(p,p).
Доказательство.Пусть Z - квадратная матрица размером 
. Тогда для матрицы X соответствующее ей отобpажение 
является аналитическим автоморфизмом области 
. Здесь E - единичная матрица размером p. Границей области 
является множество 
, которое разбивается на компоненты, различающиеся рангом матрицы (E-Z*Z), причем отображение 
ранг этой матрицы не меняет (см. [7]). Поэтому 
и при 
Осталось доказать ограниченность модуля функции на полугруппе Ольшанского. Каждая матрица 
представляется в виде 
, где 
, а 
. Поэтому 
. Отсюда
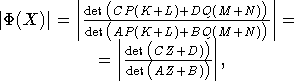
где Z=P(K+L)(M+N)-1Q-1. Заметим, что отображение (CZ+D)(AZ+B)-1 преобразует область E-Z*Z<0 в область E-Z*Z>0 и наоборот. Поэтому, чтобы доказать ограниченность Ф(X), достаточно показать, что E-Z*Z<0, т.е. что все собственные числа матрицы Z*Z больше или равны единице. А это действительно так ввиду того, что диагональные матрицы P и Q-1 состоят из чисел, больших или равных единице, а матрица (K+L)(M+N)-1 унитарная.
Для матриц из SU(p,q) при p>q требуемый пример получается ограничением указанной функции 
на группу SU(p,q).
Список литературы
Ol'shanski
G.I. Invariant cones in Lie algebras, Lie semigroups, and the holomorphic discrete series // Funct. Anal. Appl. 15 (1982), 275-285.
Lawson J.D. Semigroups of Ol'shanski type // <<Semigroups in algebra, geometry and analysis>>/ ed. Karl H. Hofmann... - Berlin; New York : de Gruyter, 1995.
Рудин У. Теоpия функций в поликруге. М.: Миp, 1974.
Koranyi A., Vagi S. Rational inner functions on bounded symmetric domains // Trans. Amer. Math. Soc., 254 (1979), 179-193.
Попов В.Л. Группы Пикара однородных пространств // Известия АН СССР. Сер. математическая. Т. 38. ò2. Март-апрель (1974). С. 296.
Владимиров В.С., Сергеев А.Г. Комплексный анализ в трубе будущего // Соврем. проблемы математики. Фунд. направления. Т. 8 (Итоги науки и техн. ВИНИТИ АН СССР). М.: 1985, С.191-266.
Пятецкий-Шапиро И.И. Геометрия классических областей и теория автоморфных функций. М.: Гос. изд-во физ.-мат. лит-ры, 1961.
Для подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/
Похожие работы
... компонентами группы . наличие в групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия. 1.3.1 Теорема. Пусть --- алгебраическая группа матриц. Её компонента , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы по (в частности, они являются связными компонентами ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... и в том случае, когда интегральный оператор (3) действует в пространстве C(W) и неразложим в этом пространстве относительно конуса неотрицательных функций пространства C(W). Получению оценок спектрального радиуса положительного оператора по информации о поведении этого оператора на фиксированном ненулевом элементе конуса посвящена достаточно обширная литература [21], [11], [13], [18], [26], ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
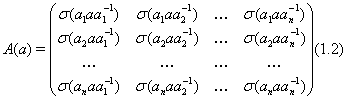
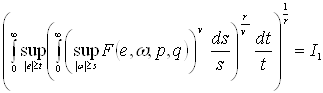
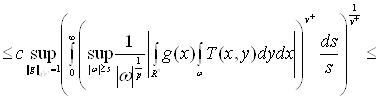
0 комментариев