Навигация
2. Доказательство теоремы 1
Нам понадобится теорема Боголюбова об острие клина (см. [6]). Приведем ее формулировку в удобной для нас форме.
Теорема 4. Пусть 
- область в 
, C - конус в . Пусть в локальных трубах 
заданы функции 
, голоморфные и ограниченные в соответствующих областях, а их граничные (предельные) значения совпадают на 
. Тогда существует комплексная окрестность 
области , и функция f, голоморфная и ограниченная в 
, совпадающая с в 
.
В нашем случае будет некоторой окрестностью в su(p,q), а будет соответствующей окрестностью в 
. Пусть внутренняя функция имеет вид 
, где (без ограничения общности) P(A), Q(A) - многочлены от элементов матрицы A такие, что [P] взаимно просто с [Q]. Пусть теперь 
. Тогда 
(см. (1.2)). Положим 
, и 
. Ввиду голоморфности экспоненциального отобpажения эти функции будут удовлетворять условиям теоремы 4. Отсюда в комплексной окрестности любой точки 
. А значит и для любой матрицы 
имеем 
, или если ввести обозначения 
и 
, то
Поскольку [P] и [Q] предполагаются взаимно простыми, то, в соответствии с теоремой 3, 
должно делиться на [Q], т.е.
Из (1) и (2) получаем, что
Заменив в (2) и (3) матрицу A на 
и перейдя к комплексно сопряж"нным выражениям, обнаруживаем, что
То есть нам удалось выделить общий множитель из двух многочленов, принадлежащих взаимно простым классам эквивалентности [P] и [Q]. Значит, этот множитель 
тривиален, т.е. 
, из чего следует, что 
. Таким образом, 
, где C - некоторая константа. Однако если 
, то
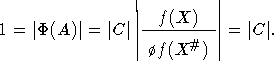
Похожие работы
... компонентами группы . наличие в групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия. 1.3.1 Теорема. Пусть --- алгебраическая группа матриц. Её компонента , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы по (в частности, они являются связными компонентами ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... и в том случае, когда интегральный оператор (3) действует в пространстве C(W) и неразложим в этом пространстве относительно конуса неотрицательных функций пространства C(W). Получению оценок спектрального радиуса положительного оператора по информации о поведении этого оператора на фиксированном ненулевом элементе конуса посвящена достаточно обширная литература [21], [11], [13], [18], [26], ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
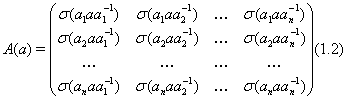
0 комментариев