Кинематический вывод преобразований Галилея

4.12 Кинематический вывод преобразований Галилея.

Введём теперь, рассуждая совершенно аналогично тому, как мы это делали при выводе формул преобразований Лоренца, формулы преобразований Галилея, изменив процедуры построения полей времени в инерциальных системах отсчета K и K ’.

Построение полей времени в системах отсчета K и K ’. Будем теперь считать, что в системе отсчёта K среда, возбуждениями которой является свет, покоится. Тогда относительно системы отсчёта K’ эта Среда будет двигаться со скоростью u в отрицательном направлении оси x’.

Процедуру построения локальных времён и синхронизации часов в системе отсчёта K оставим прежней. Но процедуру построения локальных времён в системе отсчёта K’ изменим. При синхронизации часов, помещённых в точке M но оси x’ с координатой x’M>0 , с помощью короткого импульсного светового сигнала, выпущенного из начала координат x’ = 0 в начальный момент времени t’ = 0, в момент прихода сигнала в точку M , на часах в точке M теперь поставим не время r/c , где r - расстояние между O и M , а время

 r .

c + u

Аналогично поступим с точкой M на оси x’ с координатой x’M<0. В ней на часах в момент прихода сигнала поставим время

 r .

c - u

Основные соотношения. Рассмотрим снова три мгновенных точечных события. В системе отсчёта K они выглядят следующим образом. В точке x1 на оси x в момент t’1 пусть испускается короткий световой импульс в положительном направлении оси x. В момент t’2 пусть он приходит в точку x2 на оси x, отражается в ней и в момент t’3 возвращается в точку x1 , так что x1 = x3.

Согласно принятым процедурам построения полей времени в системах отсчета K и K ’ , имеем теперь следующие шесть основных соотношений:

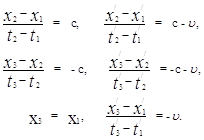
Нахождение функций j и y. Составим сначала функциональное уравнение для функции j. Имеем

Вычтем первое соотношение из третьего и результат сравним со вторым соотношением. Получим тогда уравнение

или

то есть

С учётом соотношений

отсюда приходим к следующему окончательному функциональному уравнению для определения вида функции j:

которое удовлетворяется при любых значениях независимых переменных и x1 , x2 и t1 . Чтобы разрешить это функциональное уравнение, продифференцируем его по x2 и получим из него продифференцированное функциональное уравнение:

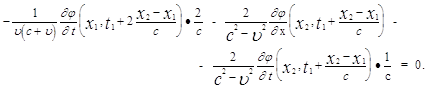
Положим в этом уравнении . x1 = x2 = x & t1 = t . Придем к уравнению

так что имеем очень простое дифференциальное уравнение

или

для определения вида функции .

Общее решение последнего уравнения имеет вид

где F - произвольная функция . Подставим эту формулу в приведенное

выше продифференцированное функциональное уравнение. Учтем ,

что

и поэтому получим соотношение

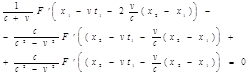
Так как

то приходим к следующему уравнению

справедливому при любых значениях x1,x2,t1. Аргументы функций

в правой и левой частях принимают произвольные значения при произвольных

x1,x2,t1. Следовательно ,

а потому , игнорируя получаем

где - некоторые пока не определенные постоянные .

Составим теперь функциональное уравнение для функции . Имеем

где G - произвольная функция . Вычитая первое уравнение из третьего

уравнения и сравнивая полученный результат со вторым уравнением ,

получаем соотношение Следовательно ,

или

Отсюда непосредственно приходим к следующему основному функциональному

уравнению для функции  :

Разрешим это уравнение , для чего сначала продифференцируем его

по x2 . Тогда получим уравнение

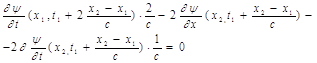Полагая в этом последнем уравнении и, приходим к

дифференциальному уравнению

или совсем простому уравнению

Следовательно ,

Подставив эту формулу для в приведенное выше продифференцированное

функциональное уравнение . Получим

Следовательно ,

Так как величины  совершенно произвольны , то аргументы

функций G в правой и левой частях могут принимать совершенно произвольные значения . Поэтому

а следовательно ,

где  - пока произвольные постоянные .

Определение констант Мы получили следующие формулы

преобразования координат и времен мгновенного точечного события :

Найдем константы

начнем с того , что выставим требование о согласовании начал отчетов

координат и времени в обеих системах отсчета  и  .

Требование 1. Событие , имеющее координаты 0 , 0 в системе отсчета  ,

имеет координаты 0 , 0 в системе отсчета  , и наоборот .

Следовательно , в приведенных формулах , и формулы

преобразования приобретают следующий вид :

Приведенные формулы преобразования мы получили как следствия

наших шести основных соотношений . В них входят пока не определенные

нами величины и.

Подставив эти формулы преобразования обратно в исходные шесть

соотношений , мы можем найти ограничения на константы и. Так

собственно говоря и получается . Действительно , имеем равенства

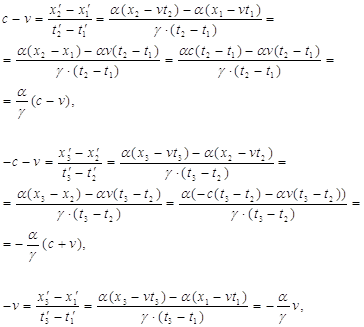
Как видим , чтобы эти равенства выполнялись , необходимо потребовать ,

чтобы константы и были равны друг другу :

Таким образом , искомые формулы преобразования координат мгновенного

точечного события имеют вид

где - пока не определенная константа .

Как и в случае преобразований Лоренца , воспользуемся тем , что

у нас имеется произвол в выборе единиц измерения либо длинны , либо

времени в обеих системах отсчета  и . Чтобы фиксировать указанный произвол , выставим дополнительное требование .

Требование 2. Длина l движущегося в системе  стержня , покоящегося

в системе  , ориентированного вдоль оси и имеющего в этой системе длину , т.е. .

Рассмотрим движущийся стержень , все время покоящийся в системе отсчета

 между точками от  с координатами  и .

Пусть в одинаковые локальные моменты времени в системе отсчета

K левый конец стержня совпал с точкой оси x , с координатой(событие A), (событие B). Тогда

Вычитая второе равенство из первого , с учетом условия получаем

и так как согласно требованию 2 , то приходим к заключению ,

что

Итак , мы вывели с помощью исключительно кинематических рассуждений ,

аналогичных использованным Эйнштейном при выводе формул преобразований Лоренца , формулы преобразований Галилея :

Похожие работы

Курс лекций по физике

Скачать

27693

7

32

... свойства. А.у.т. - тело, для которого силы однозначно определяют деформации и наоборот. Правильность выбранной абстракции подтверждается совпадением, определенной точностью результатов теории и опыта. Физика - наука, устанавливающая закономерные связи посредством наблюдений явлений в природе и посредством лабораторных опытов. Согласие результатов научного анализа с результатами опыта - критерий ...

Физики продолжают шутить

Скачать

25258

0

3

... так, как большинство материалов относится к устному творчеству, откуда и были получены, также есть выдержки из книг: «Физики шутят», «Физики продолжают шутить», «Сборник задач по физике» Г. Остера. Шутки, которые шутят физики. Один математик спросил коллегу, известного своими религиозными убеждениями: - Вы, что же, верите в единого ...

Английский физик Майкл Фарадей

Скачать

27836

0

0

... фара́да). 1 фарад равен электрической ёмкости конденсатора, при которой заряд 1 кулон создаёт между обкладками конденсатора напряжение 1 вольт. Ф = Кл/В = A·c/B Единица названа в честь английского физика Майкла Фарадея Фарад — очень большая ёмкость. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Для сравнения, ёмкость Земли (шара размером с ...

Великий физик Америки

Скачать

23944

0

0

... гальванометра отклонялась (то же происходило и при поднятии электромагнита из катушки). Эта схема напоминает рисунок из лабораторного журнала Фарадея. Удивительно, как схожи оказались эксперименты двух великих физиков, работавших независимо друг от друга на разных континентах! В своей статье, написанной уже после знакомства с опытом Фарадея, Генри, отдавая должное английскому физику, подчеркнул, ...