Навигация
2. Случай.
Корни знаменателя действительные, причем некоторые из них кратные:
В этом случае дробь 
разлагается на простейшие дроби 1и 2 типов.
Пример 1.
3. Случай.
Среди корней знаменателя есть комплексные неповторяющиеся(т.е. различные):
В этом случае дробь разлагается на простейшие дроби 1,2 и 3 типов.
Пример 2.Требуется вычислить интеграл
.Разложим подынтегральную дробь на простейшие:
Следовательно,
.
Полагая х=1, получим 1=2С, С= ½; полагая х=0, получим 0= -B+C, B=1/2.
Приравнивая коэффициенты при 
, получим 0=А+С, откуда А= - ½. Таким образом ,
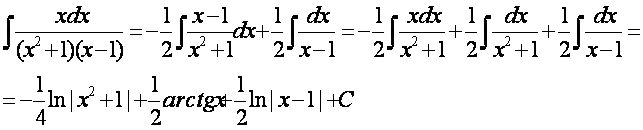
4. Случай.
Среди корней знаменателя есть комплексные кратные:
В этом случае разложение дроби будет содержать и простейшие дроби 4 типа.
Пример 3. Требуется вычислить интеграл
.
Решение. Разлагаем дробь на простейшие:
откуда
Комбинируя указанные выше методы определения коэффициентов, находим А=1, В= - 1, С=0, D=0, Е=1.
Таким образом, получаем
Из всего изложенного следует, что интеграл от любой рациональной функции может быть выражен через элементарные функции в конечном виде, а именно:
через логарифмы- в случаях простейших дробей 1 типа;
через рациональные функции- в случае простейших дробей 2 типа
через логарифмы и арктангенсы- в случае простейших дробей 3 типа
через рациональные функции и арктангенсы- в случае простейших дробей 4 типа.
Интегралы от иррациональных функций
Не от всякой иррациональной функции интеграл выражается через элементарные функции. Сейчас мы рассмотрим те иррациональные функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, до конца интегрируются.
1.Рассмотрим интеграл 
, где R-рациональная функция своих аргументов [1] ).
Пусть R-общий знаменатель дробей m/n,…r/s.Сделаем подстановку 
.Тогда каждая дробная степень х выразится через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию от t.
Пример 1. Требуется вычислить интеграл
.
Решение. Общий знаменатель дробей 1/2,3/4, есть 4; поэтому делаем подстановку 
; тогда
=
.
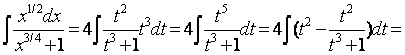
2.Рассмотрим теперь интеграл вида
Этот интеграл сводится к интегралу от рациональной функции с помощью подстановки
где 
- общий знаменатель дробей m/n,…r/s.
Пример 2. Требуется вычислить интеграл
.
Решение. Делаем подстановку 
тогда
=
Похожие работы
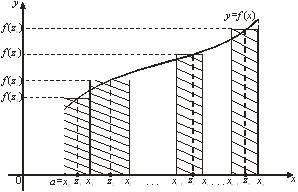
... дробей m и n; 2) если Z, то используется подстановка: a+bxn=ts, где s – знаменатель дроби 3) если Z, то применяется подстановка: ax-n+b=ts, где s – знаменатель дроби 9. Понятие определенного интеграла, его геометрический смысл. Определение. Если существует конечный передел интегральной суммы (8) - (8) при λ→0, не зависящий от способа разбиения &# ...
... предел функции Решение: Имеем неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель , который при не равен нулю. В результате неопределенность будет раскрыта. 2. Производная и дифференциал Пусть функция определена в некоторой окрестности точки . Производной функции в точке называется предел отношения , когда ( ...
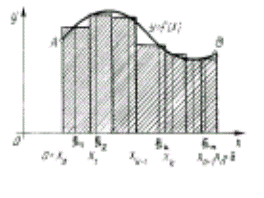
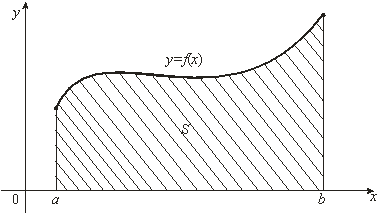
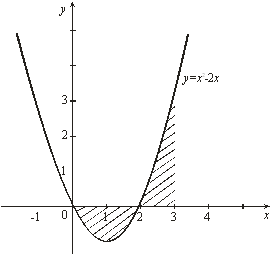
... выражением, – переменной интегрирования; отрезок называется промежутком интегрирования. Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке. 2. Геометрический смысл определенного интеграла Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью ...
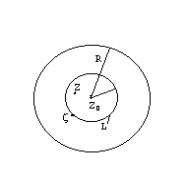
... переменных Z и z при произвольном изменении области G и переменных на кривой С. Очевидно, что при сделанных предположениях : Интеграл существует и является функцией комплексной переменной. Справедлива формула : (2) Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру. ТЕОРЕМА. Пусть f(Z) ...
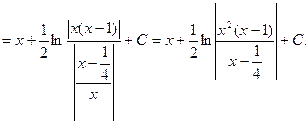
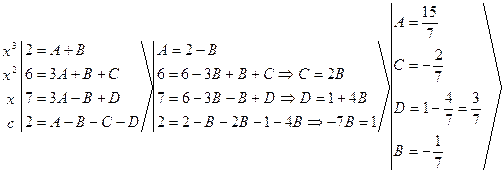
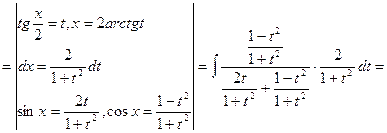
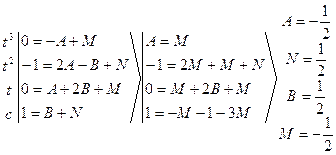
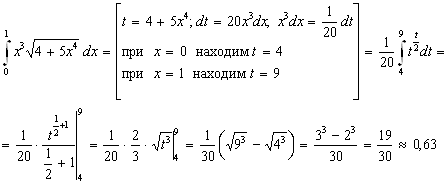
0 комментариев