Навигация
Определенный интеграл
Содержание
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площадь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Литература
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
Пусть функция ![]() определена на отрезке
определена на отрезке ![]() ,
, ![]() . Выполним следующие операции:
. Выполним следующие операции:
1) разобьем отрезок ![]() точками
точками ![]() на n частичных отрезков
на n частичных отрезков ![]() ;
;
2) в каждом из частичных отрезков ![]() ,
, ![]() выберем произвольную точку
выберем произвольную точку ![]() и вычислим значение функции в этой точке:
и вычислим значение функции в этой точке: ![]() ;
;
3) найдем произведения ![]() , где
, где ![]() – длина частичного отрезка
– длина частичного отрезка ![]() ,
, ![]() ;
;
4) составим сумму
 , (1)
, (1)
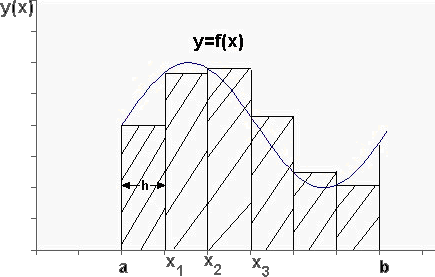
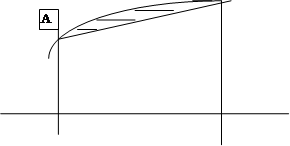
которая называется интегральной суммой функции y = f(x) на отрезке [а, b]. С геометрической точки зрения интегральная сумма ![]() представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки ![]() , а высоты равны
, а высоты равны ![]() соответственно (рис. 1). Обозначим через
соответственно (рис. 1). Обозначим через ![]() длину наибольшего частичного отрезка
длину наибольшего частичного отрезка ![]() ;
;
5) найдем предел интегральной суммы, когда ![]() .
.
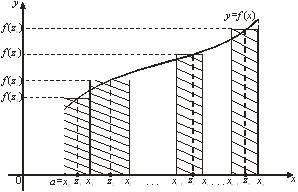
Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка ![]() на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек ![]() в них, то этот предел называется определенным интегралом от функции
в них, то этот предел называется определенным интегралом от функции ![]() на отрезке
на отрезке ![]() и обозначается
и обозначается 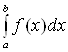 .
.
Таким образом, 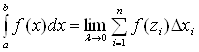 .
.
В этом случае функция ![]() называется интегрируемой на
называется интегрируемой на ![]() . Числа а и b называются соответственно нижним и верхним пределами интегрирования,
. Числа а и b называются соответственно нижним и верхним пределами интегрирования, ![]() – подынтегральной функцией,
– подынтегральной функцией, ![]() – подынтегральным выражением,
– подынтегральным выражением, ![]() – переменной интегрирования; отрезок
– переменной интегрирования; отрезок ![]() называется промежутком интегрирования.
называется промежутком интегрирования.
Теорема 1. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Похожие работы
... с содержится в промежутке . Таким образом, мы вновь получили лангранжеву форму дополнительного члена. 5. Заключение. В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой ...
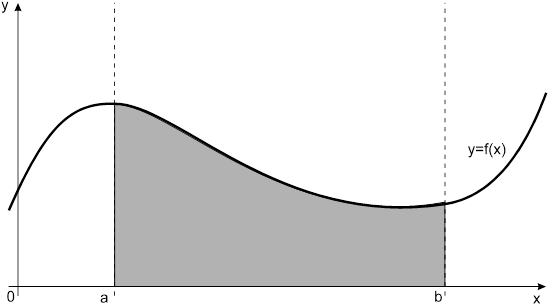
ределенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). Рис. 1. Криволинейная трапеция. Рис. 2. Метод трапеций. Рис. 3. Метод средних прямоугольников. По методам ...
... n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 f(x)= x3 f(x)= x4 на отрезке [0, 1] с шагом , , 2. f(x)= f(x)= f(x)= ...
... ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...


0 комментариев