Навигация
Рассмотрим примеры тождественных преобразований дробно-рациональных выражений
13480
знаков
0
таблиц
9
изображений
3. Рассмотрим примеры тождественных преобразований дробно-рациональных выражений.
При выполнении Т.П. таких выражений надо следить за областью определения выражения, т.к. может происходить расширение области определения. Это может произойти, например, при сокращении дроби.
Так область определения дроби
все х¹1 и х¹ –2.
Вместе с тем 
.
Сократив дробь, получим 
. Область определения полученной дроби: х¹-2, т.е шире, чем О.О. первоначальной дроби.
Поэтому дроби и равны при х¹1 и х¹-2.
Изменение области определения выражения возможно и в результате некоторых других преобразований, поэтому, выполнив преобразования выражения, нужно всегда уметь ответить на вопрос, на каком множестве оно тождественно полученному.
Пример 1. Сократить дробь 
Решение:
1) Найдем О.О. Для этого нужно потребовать, чтобы знаменатель дроби был отличен от 0. a+b¹0 Þ a¹b. Таким образом О.О. f(a) все a¹b.
2) Чтобы сократить дробь, разложим числитель на множители
2а2+ab-b2=2a2+2ab-ab-b2=(2a2+2ab)+(-ab-b2)=2a(a+b)-b(a+b)=(a+b)(2a-b)
3) 
Ответ: 
.
Пример 2. Упростить выражение
Решение:
Найдем область определения: а2+3а+2¹0, а2+4а+3¹0, а2+5а+6¹0.
Используя т. Виета найдем значения а, при которых трехчлены обращаются в нуль
а2+3а+2=0 при а1=–2, а2=–1
а2+4а+3=0 при а1=–3, а2=–1
а2+5а+6=0 при а1=–3, а2=–2
таким образом область определения f(а): а¹–2, а¹–1, а¹–3
Приведем сумму дробей, стоящую в скобках, к общему знаменателю, предварительно определив его, используя 1)
а2+3а+2=(а+2)(а+1)
а2+4а+3=(а+3)(а+1)
а2+5а+6=(а+3)(а+2) тогда общий знаменатель: (а+2)(а+3)(а+1).
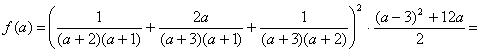
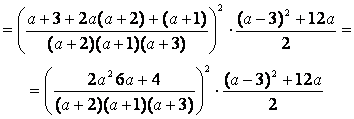
Разложим числитель первой и второй дроби на множители:
2а2+6а+4=2(а2+3а+2)=2(а+2)(а+1)
(а–3)2+12а=а2–6а+9+12а=а2+6а+9=(а+3)2
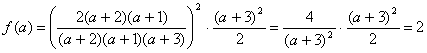
Ответ: 
при а¹–3, а¹–2, а¹–1.
Пример 3. Упростить выражение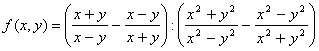 
Решение:
Найдем область определения:
х–у¹0 Þ х¹у
х+у¹0 Þ х¹–у
х2–у2¹0 Þ х¹у, х¹–у
х2+у2¹0 Þ х¹0, у¹0.
Итак, область определения х¹0, у¹0, х¹у, х¹–у.
Приведем дроби, стоящие в скобках к общему знаменателю и воспользуемся формулами сокращенного умножения
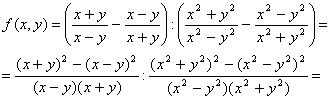
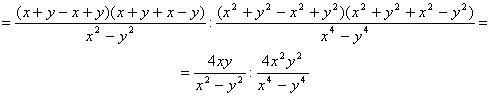
Воспользуемся правилом деления дробей: 
Ответ: 
при х¹0, у¹0, х¹у, х¹–у.
Пример 4. Упростить выражение
Найдем область определения выражения:
а¹0 Þ
b+с¹0 Þ b¹–с
Þ b+с–а¹0 Þ b+с¹а
а¹0 и b+с¹0
2bс¹0 Þ b¹0, с¹0.
Таким образом, область определения: а¹0, b¹0, с¹0, b¹–с, b+с¹а.
Приведем дроби, стоящие в числителе и знаменателе первой дроби, а также сумму, стоящую в скобках, к общим знаменателям
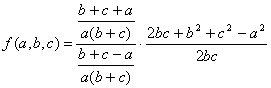
Воспользуемся правилом деления дробей и приведем четырехэтажную дробь к двухэтажной. В числителе второй дроби выделим полный квадрат суммы b и с
Числитель второй дроби, воспользовавшись формулой разности квадратов, разложим на множители
Ответ: 
при а¹0, b¹0, b¹–с, с¹0, b+с¹а.
Пример 5. Упростить выражение
Найдем область определения выражения, для этого потребуем
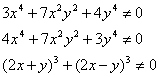
первые два выражения, как сумма трех неотрицательных слагаемых равны нулю только при х=0 и у=0.
Рассмотрим третье выражение
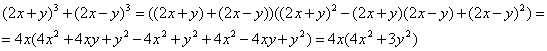
тогда 
когда 
. Отсюда имеем х¹0, у¹0.
Т.о. обл. определения х¹0, у¹0.
2) Знаменатель третьей дроби мы заложили на множители, находя область определения выражения. Разложим на множители числитель первой дроби, а в числителе и в знаменателе второй представим
Воспользуемся правилами деления дробей
Ответ: 
Пример 6. Упростить выражение 
Решение:
Найдем область определения:
b-c ¹ 0 Þ b ¹ c
c-a ¹ 0 Þ c ¹ a
a-b ¹ 0 Þ a ¹ b
2) Приведем дроби к общему знаменателю (b-c)(c-a)(a-b)
3) Воспользуемся формулами сокращенного умножения
Ответ: f(a,b,c) = 0 при b ¹ c, c ¹ a, a ¹ b.
4. Для успешного выполнения тождественных преобразований иррациональных выражений нужно помнить:
1. Определение арифметического корня n-ой степени:
Если 
и n – натуральное число большее 1, то существует только одно неотрицательное число x такое, что выполняется равенство 
. Это число х называется арифметическим корнем n-ой степени из неотрицательного числа а и обозначается 
.
Пример.
Если n – нечетное натуральное число большее 1 и а < 0, то под 
понимают такое отрицательное число х, что 
.
Пример. 
2. Из определения 1. Следует, что если в алгебраическом выражении есть корни четной степени, то подкоренные выражения таких корней должны быть неотрицательными, что учитывается при определении области определения алгебраического выражения.
Пример. 
Область определения выражения 
Похожие работы
... функций, имеющих одинаковое основание, симметричны относительно прямой (рис. 3). Рис. 3 Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике. Задание 1. Вычислите: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Решение: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Ответ: ; ; ; ; . Задание 2. Упростите выражения: 2.1) ; ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... и приемлемым для выполнения следующего действия, где это значение используется (т.е. некоторые величины в выражении будут случайными, другие — вычисляемыми); 3) при записи десятичной дроби в школьной математике используется десятичная запятая, а при записи на компьютере — десятичная точка; 4) если в записи выражения используются десятичные дроби, то они должны быть несократимыми и правильными. ...
... образом, обращение с числовым рядом как с величиной позволяет по новому формировать сами навыки сложения-вычитания (а затем умножения-деления). Глава II. Методические рекомендации к изучению алгебраического материала в начальной школе 2.1 Обучение в начальной школе с точки зрения потребностей средней школы Как известно, при изучении математики в 5-м классе существенная часть времени ...
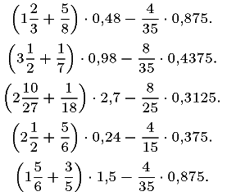
0 комментариев