Навигация
3. Определение модуля числа.
Модулем числа а называется само число а, если 
и противоположное ему число, если а < 0 т.е. 
4. Свойства арифметического корня:
Если n, k, m – натуральные числа, 
то:
1° 
2°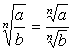 
, если b ¹ 0.
Замечание. Если a < 0, b < 0, то свойства 1° и 2° принимают вид
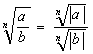
3° 
4° 
5° 
6° 
Замечание. Если показатели корней нечетные числа, то свойства 1°– 6° выполняются для a < 0, b < 0 и ab < 0.
7° Если n – четное число т.е. n = 2k, то 
Пример. 
т.к. 
, то 
, тогда по определению модуля 
и 
.
Пример 1. Упростить выражение: 
Решение.
1) Сначала, используя свойства арифметического корня, упростить каждый из имеющихся радикалов:
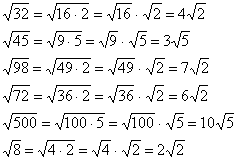
2) 
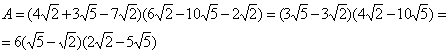
3) Раскроем скобки и приведем подобные
Ответ: 
Пример 2. Упростить выражение 
Решение: Выражение упростится, если окажется, что под этим корнем содержится полный квадрат разности или суммы каких-нибудь чисел.
Представим 
в виде полного квадрата. Для этого представим
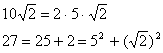тогда 
2) 
3) По свойству 7° имеем 
Т.к. 
, то 
, тогда по определению модуля
и 
Ответ: 
.
Пример 3. Освободиться от иррациональности в знаменателе дроби
.
Решение:
В знаменателе имеем иррациональность 2-ой степени, поэтому домножим и числитель, и знаменатель дроби на сумму чисел 
и 
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
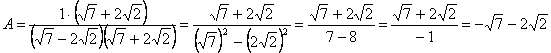
Ответ: 
.
Пример 4. Освободиться от иррациональности в знаменателе дроби
Решение:
Имеем иррациональность 3-ей степени, поэтому и числитель, и знаменатель умножим на неполный квадрат чисел 
и 1, тогда в знаменателе получим разность кубов, которая и ликвидирует иррациональность.
Ответ: 
Пример 5. Упростить выражения
Решение:
Воспользуемся свойствами степени с рациональным показателем и арифметического корня
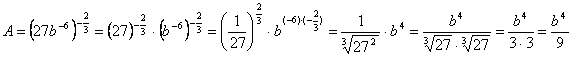
Ответ: 
.
Решение:
От десятичных дробей в показателе степени перейдем к обыкновенным и воспользуемся свойствами арифметического корня и степени с рациональным показателем
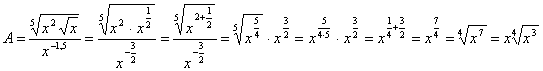
Ответ: 
.
Пример 6. Упростить выражение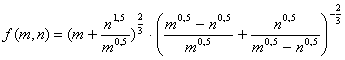 
Решение:
1. Найдем область определения алгебраического выражения
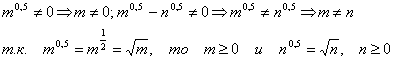
в результате имеем 
.
Похожие работы
... функций, имеющих одинаковое основание, симметричны относительно прямой (рис. 3). Рис. 3 Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике. Задание 1. Вычислите: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Решение: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Ответ: ; ; ; ; . Задание 2. Упростите выражения: 2.1) ; ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... и приемлемым для выполнения следующего действия, где это значение используется (т.е. некоторые величины в выражении будут случайными, другие — вычисляемыми); 3) при записи десятичной дроби в школьной математике используется десятичная запятая, а при записи на компьютере — десятичная точка; 4) если в записи выражения используются десятичные дроби, то они должны быть несократимыми и правильными. ...
... образом, обращение с числовым рядом как с величиной позволяет по новому формировать сами навыки сложения-вычитания (а затем умножения-деления). Глава II. Методические рекомендации к изучению алгебраического материала в начальной школе 2.1 Обучение в начальной школе с точки зрения потребностей средней школы Как известно, при изучении математики в 5-м классе существенная часть времени ...
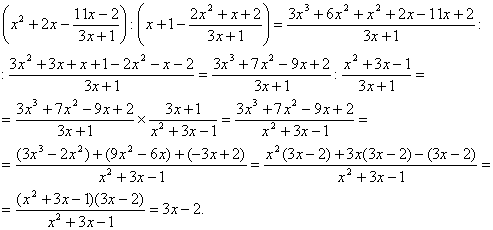
0 комментариев