Навигация
Перейдем в показателях степеней от десятичных дробей к обыкновенным и выражения, стоящие в скобках приведем к общему знаменателю
13480
знаков
0
таблиц
9
изображений
2. Перейдем в показателях степеней от десятичных дробей к обыкновенным и выражения, стоящие в скобках приведем к общему знаменателю
3. Числитель первой дроби преобразуем как сумму кубов
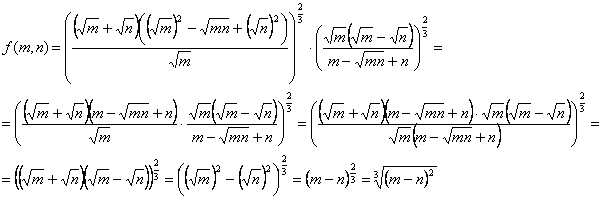
Пример 6. Упростить выражение 
Решение:
Приведем дроби, стоящие под знаками корня к общему знаменателю
В числителе первой дроби стоит полный квадрат суммы, а в числителе второй дроби – полный квадрат разности 
и 
: 
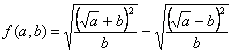
3. Воспользуемся свойством арифметического корня
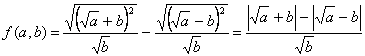
4. Так как 
и 
, то 
, а значит 
.
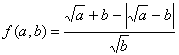
5. Так как 
может быть как отрицательным, так и положительным, рассмотрим два случая:
1) 
, тогда 
. В этом случае 
и
2) 
, тогда 
.
В этом случае 
и
Ответ: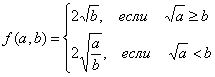 
.
Контрольное задание.
Предлагаем для самостоятельного решения приведенные ниже задачи. Желательно решить все задачи, однако, если это не удалось, присылайте только те, которые решены.Правила оформления работ смотрите во вступительной статье.
Разложить на множители
М8.1.1. 
М8.1.2. 
М8.1.3. 
М8.1.4. 
Сократить дробь
М8.1.5. 
М8.1.6. 
Упростить выражение
М8.1.7.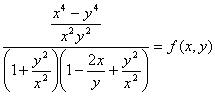 
М8.1.8.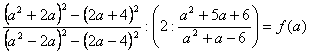 
М8.1.9. 
М8.1.10. Избавиться от иррациональности в знаменателе дроби 
Упростить выражение
М8.1.11. 
М8.1.12. 
М8.1.13.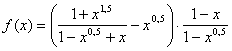 
М8.1.14.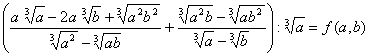 
М8.1.15.
Похожие работы
... функций, имеющих одинаковое основание, симметричны относительно прямой (рис. 3). Рис. 3 Глава 3. Тождественные преобразования показательных и логарифмических выражений на практике. Задание 1. Вычислите: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Решение: 1.1) ; 1.2) ; 1.3) ; 1.4) ; 1.5) . Ответ: ; ; ; ; . Задание 2. Упростите выражения: 2.1) ; ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... и приемлемым для выполнения следующего действия, где это значение используется (т.е. некоторые величины в выражении будут случайными, другие — вычисляемыми); 3) при записи десятичной дроби в школьной математике используется десятичная запятая, а при записи на компьютере — десятичная точка; 4) если в записи выражения используются десятичные дроби, то они должны быть несократимыми и правильными. ...
... образом, обращение с числовым рядом как с величиной позволяет по новому формировать сами навыки сложения-вычитания (а затем умножения-деления). Глава II. Методические рекомендации к изучению алгебраического материала в начальной школе 2.1 Обучение в начальной школе с точки зрения потребностей средней школы Как известно, при изучении математики в 5-м классе существенная часть времени ...
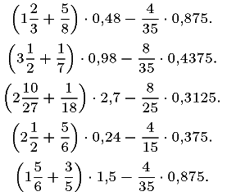
0 комментариев