Навигация
Моделирование случайной величины
4. Моделирование случайной величины
абсолютно непрерывного типа
А. Метод обратных функций.
Пусть случайная величина ![]() имеет монотонно возрастающую функцию распределения
имеет монотонно возрастающую функцию распределения ![]() . Известно, что
. Известно, что ![]() значит, случайная величина
значит, случайная величина ![]() с монотонно возрастающей функцией распределения
с монотонно возрастающей функцией распределения ![]() связана со случайной величиной
связана со случайной величиной ![]() соотношением
соотношением
![]() .
.
Отсюда следует, что значение ![]() случайной величины
случайной величины ![]() является решением уравнения
является решением уравнения
![]() , (3)
, (3)
где ![]() — значение случайной величины
— значение случайной величины ![]() т. е.
т. е.
![]() .
.
Последовательности значений ![]() случайной величины
случайной величины ![]() соответствует последовательность
соответствует последовательность ![]() значений случайной величины
значений случайной величины ![]() с функцией распределения
с функцией распределения ![]() .
.
Б. Моделирование случайной величины с равномерным распределением на отрезке ![]() .
.
Пусть случайная величина ![]() имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке ![]() . Тогда ее функция распределения имеет вид:
. Тогда ее функция распределения имеет вид:
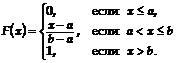 .
.
Составим уравнение (3), получим
![]() ,
,
откуда
![]() .
.
Последовательности значений ![]() случайной величины
случайной величины ![]() соответствует последовательность значений
соответствует последовательность значений
![]() ,
, ![]() , …
, …
случайной величины ![]() равномерно распределенной на отрезке
равномерно распределенной на отрезке ![]() .
.
В. Моделирование случайной величины с показательным распределением.
Пусть случайная величина ![]() имеет показательное распределение с параметром
имеет показательное распределение с параметром ![]() . Тогда функция распределения этой случайной величины
. Тогда функция распределения этой случайной величины
![]() ,
, ![]() .
.
Составим уравнение (3). Имеем
![]() . (4)
. (4)
Решаем уравнение (4) относительно ![]() получаем
получаем
![]() . (5)
. (5)
Так как ![]() — случайная величина, равномерно распределенная на
— случайная величина, равномерно распределенная на ![]() , то и
, то и ![]() является также случайной величиной, распределенной по равномерному закону на отрезке
является также случайной величиной, распределенной по равномерному закону на отрезке ![]() . Поэтому вместо формулы (5) для моделирования случайной величины
. Поэтому вместо формулы (5) для моделирования случайной величины ![]() можно использовать формулу
можно использовать формулу
![]() .
.
Г. Моделирование случайной величины с нормальным распределением.
Случайная величина ![]() имеет нормальный закон распределения, если ее функция распределения имеет вид:
имеет нормальный закон распределения, если ее функция распределения имеет вид:
![]() ,
,
где ![]() и
и ![]() — параметры.
— параметры.
Для компьютерного моделирования случайной величины с нормальным законом распределения можно использовать как метод обратных функций, так и метод, специально разработанный для нормального закона.
Согласно центральной предельной теореме, если случайные величины ![]() независимы, одинаково распределены и их математическое ожидание и дисперсия конечны, то при увеличении
независимы, одинаково распределены и их математическое ожидание и дисперсия конечны, то при увеличении ![]() закон распределения суммы
закон распределения суммы
![]()
приближается к нормальному. Требуется найти значения случайной величины ![]() распределенной по нормальному закону с математическим ожиданием
распределенной по нормальному закону с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() .
.
Пусть ![]() — независимые случайные величины, равномерно распределенные на отрезке
— независимые случайные величины, равномерно распределенные на отрезке ![]() . Обозначим
. Обозначим
![]() . (6)
. (6)
Учитывая ![]()
![]()
![]() , найдем:
, найдем:
![]()
![]() .
.
При достаточно большом ![]()
![]() можно считать, что случайная величина
можно считать, что случайная величина ![]() имеет нормальный закон распределения с математическим ожиданием
имеет нормальный закон распределения с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() .
.
Пронормируем случайную величину ![]() , получим:
, получим:
![]() . (7)
. (7)
Для случайной величины ![]() имеет место
имеет место
![]() ,
, ![]() .
.
Перейдем от случайной величины ![]() к стандартной нормально распределенной случайной величине
к стандартной нормально распределенной случайной величине
![]() .
.
Тогда
![]() .
.
Учитывая (6) и (7), получаем:
![]()
Например, при ![]()
![]() .
.
Отсюда значение ![]() случайной величины
случайной величины ![]() определится по формуле
определится по формуле
![]() , (8)
, (8)
где ![]() — значения случайной величины
— значения случайной величины ![]() , равномерно распределенной на отрезке
, равномерно распределенной на отрезке ![]() .
.
Таким образом, имея 12 значений случайной величины ![]() и подставляя их в формулу (8), получаем значение случайной величины
и подставляя их в формулу (8), получаем значение случайной величины ![]() имея следующие 12 значений величины
имея следующие 12 значений величины ![]() и подставив их в формулу (8), получим следующее значение случайной величины
и подставив их в формулу (8), получим следующее значение случайной величины ![]() и т. д.
и т. д.
1. Калинина В.Н., Панкин В.Ф. Математическая статистика. М.: Высш. шк., 2001.
2. Кретов М.В. Вероятностные методы оценки прочности строительных материалов // Международная научная конференция «Инновация в науке и образовании—2003». Калининград, 2003. С. 228.
3. Кретов М.В. Теория вероятностей и математическая статистика. Калининград: Янтарный сказ, 2004.
4. Нейман Ю. Вводный курс теории вероятностей и математической статистики. М.: Наука, 1
Похожие работы
... 2. Таблица 2. Устранение недостатков анализа чувствительности и анализа сценариев при использовании для риск-анализа метода Монте-Карло Метод Недостаток Решение с помощью имитационного моделирования Анализ чувствительности Не учитывается наличие корреляции между различными составляющими проекта Корреляция моделируется различными методами и учитывается в модели Рассматривается влияние ...
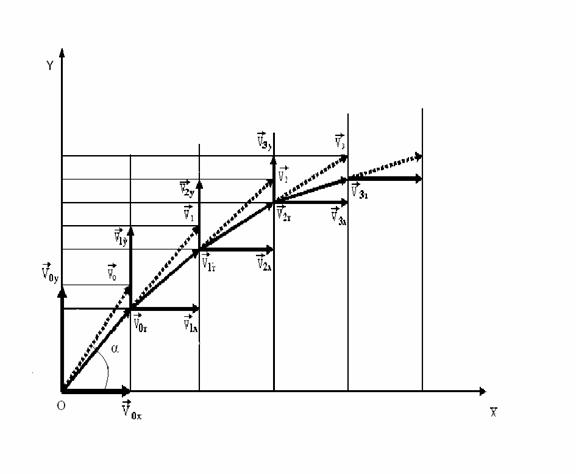
... порыв ветра, интенсивность горения пороха, влажность и т.д. Из всех случайных величин рассмотрим только сопротивление воздуха. Учитывая то, что сопротивление воздуха направленно в противоположную сторону движения тела [4], то силу сопротивления можно представить в виде двух составляющих: вертикальной и горизонтальной, при этом, чем выше скорость, тем больше сопротивление и наоборот. Выделим ...
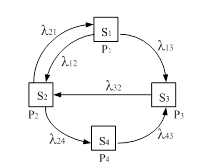
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... тех же условий анализа. Так, в точке эквивалентности при титровании 0,01 М AgNO3 глицином величина рAg оказалaсь: по потенциометрическим данным - 4,2, по результатам компьютерного моделирования - 3,5; соответственно при титровании 0,0010 М AgNO3 комплексоном III - 5,6 и 4,9. Невелики (менее 10%) и расхождения по объему титранта, соответствующему точке эквивалентности. Отмеченные расхождения можно ...


0 комментариев