Построение статической характеристики объекта
Аппроксимация полиномом второго порядка
Расчет коэффициентов передачи
Модель объекта первого порядка без запаздывания
Модель объекта первого порядка с запаздыванием
Построение математической модели
Выбор и расчет параметров настройки регуляторов
Расчет ПИ-регулятора
Обзор методов исследования на устойчивость
Проверка устойчивости по критерию Рауса
Проверка устойчивости по корням характеристического уравнения
Оценка качества функционирования АСР
Навигация
Проверка устойчивости по корням характеристического уравнения
Автоматическая система регулирования с П-регулятором
45149
знаков
18
таблиц
55
изображений
8.3 Проверка устойчивости по корням характеристического уравнения
Ниже приведены результаты проверки устойчивости замкнутых систем по корням характеристического уравнения на ЭВМ в системе MathCad.
9. Приведение к системе дифференциальных уравнений
Система дифференциальных уравнений устанавливает связь выходной координаты с входными в переходном процессе. То есть если передаточная характеристика системы имеет вид:
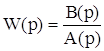
то связь выходной координаты с входной можно записать так:
.
Для приведения к системе дифференциальных уравнений выполняем следующие действия:
- все члены правой части переносим в левую часть и группируем члены с одинаковыми порядками производных:
;
- формально интегрируем полученное уравнение (порядок уравнения во всех членах уменьшается на 1). Интегрирование выполняется до тех пор, пока не исчезнут все р в левой части.
9.1 Система с П-регулятором
Передаточной функцией системы автоматического регулирования с П-регулятором по возмущению является найденное ранее выражение:
Тогда в соответствии с вышеизложенным, запишем:
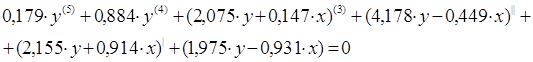
пусть 
;
обозначим 
, тогда
Тогда окончательно система запишется следующим образом:
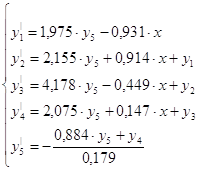
Передаточная функция системы с П-регулятором по управлению:
Тогда в соответствии с вышеизложенным, запишем нормальную систему:
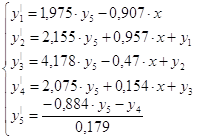
9.2 Система с И-регулятором
Передаточная функция системы с И-регулятором по возмущению:
Тогда в соответствии с вышеизложенным, запишем нормальную систему:
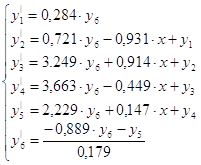
Передаточная функция системы с И-регулятором по управлению:
Тогда в соответствии с вышеизложенным, запишем нормальную систему:
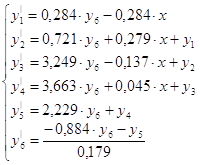
9.3 Система с ПИ-регулятором
Передаточная функция системы с ПИ-регулятором по возмущению:
Тогда в соответствии с вышеизложенным, запишем нормальную систему:
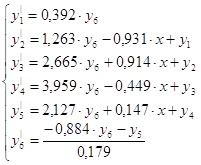
Передаточная функция системы с ПИ-регулятором по управлению:
Тогда в соответствии с вышеизложенным, запишем нормальную систему:
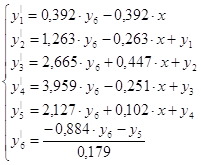
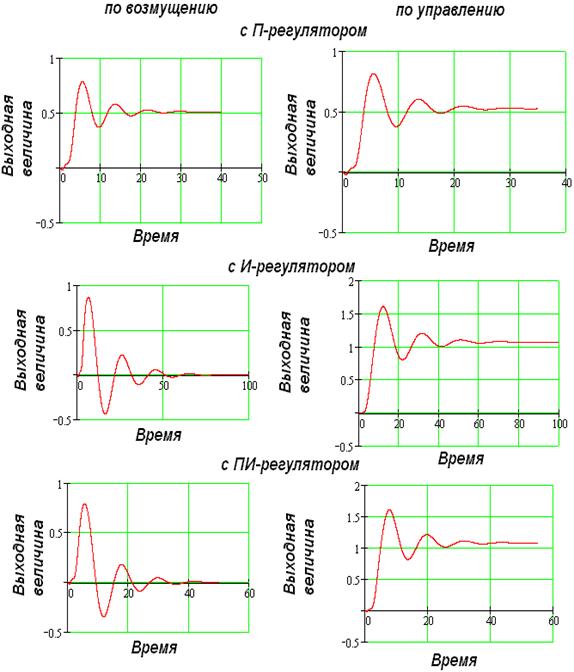
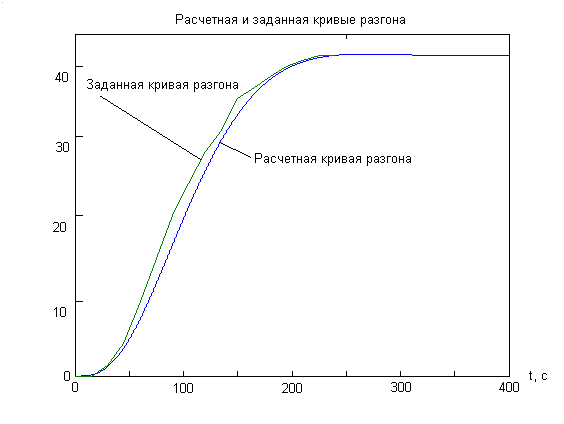
10. Построение переходных процессов
Несмотря на то, что ряд оценок качества функционирования АСР могут быть вычислены без построения таблиц и графиков переходных процессов, тем не менее, окончательный ответ о пригодности системы можно получить только по результатам исследования переходных процессов. Поэтому на завершающей стадии проектирования АСР всегда стремятся тем или иным способом получить оценки динамических характеристик системы и сравнить их с заданными.
Переходные процессы рассчитывают для замкнутых АСР по возмущающему или управляющему воздействиям. Если по возмущению, то регулятор должен в течении переходного процесса компенсировать это возмущение, а объект - возвратиться в то же состояние, в котором он был до приложения возмущения. Если по управлению, то регулятор должен отработать управляющее воздействие и регулируемая величина на выходе объекта должна принять новое, заданное значение.
При использовании для построения переходных процессов любых методов (аналитические, численные) в качестве исходного материала необходимо иметь математическую модель замкнутой системы в форме передаточной функции, дифференциального уравнения или уравнений АФХ, которые можно получить из передаточной функции.
Если передаточная функция замкнутой системы приведена к дифференциальному уравнению с произвольной правой частью, то аналитическое решение ищется в такой последовательности:
- находятся корни характеристического уравнения;
- строится частное решение с неопределенными коэффициентами;
- это частное решение подставляется в исходное уравнение;
- посредством приравнивания коэффициентов при одинаковых степенях х находятся все неопределенные коэффициенты;
- записывается искомое частное решение.
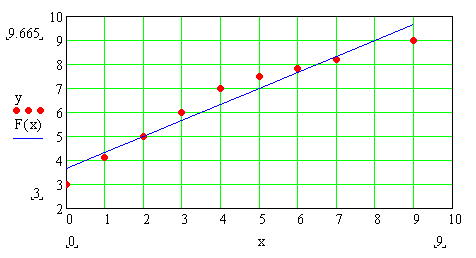
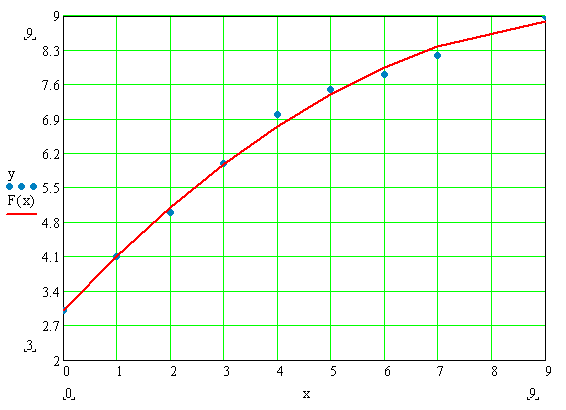
Это решение и будет являться зависимостью выходной координаты системы от времени.
При использовании численных методов для построения переходных процессов необходимо:
- передаточную функцию замкнутой системы преобразовать в дифференциальное уравнение, разложив при этом звено запаздывания в ряд Паде;
- дифференциальное уравнение n порядка привести к системе из n дифференциальных уравнений первого порядка;
- задать уравнение для возмущающего воздействия;
- выбрать один из численных методов для решения полученной системы; предпочтительнее методы с итерационным уточнением решения на каждом шаге (усовершенствованный метод Эйлера-Коши) или с автоматическим выбором величины шага для обеспечения требуемой точности (метод Рунге-Кутта);
- составить программу для ЭВМ или использовать стандартную из состава математического обеспечения.
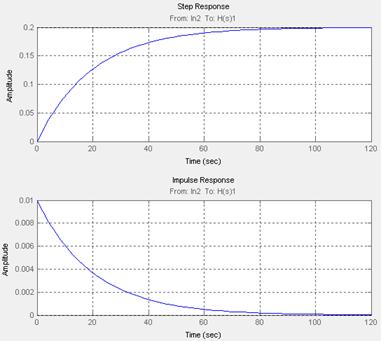
Ниже представлены графики переходных процессов по управлению и возмущению систем с П, И и ПИ-регуляторами. Графики построены в системе MathCad.
Похожие работы
... свойства объекта управления остаются, практически неизменными. Поэтому изучение характеристик объекта управления относятся к одной из основных задач теории автоматического управления и регулирования. В данной курсовой работе Я разрабатываю АСР для молотковой дробилки типа ДДМ-1, в соответствии с требованием данной технологии. Обеспечить оптимальный режим работы в выборе типа регулятора и закона ...
... ИССЛЕДОВАНИЕ НА УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 7.1 Постановка задачи Система автоматического регулирования как динамическая система, характеризуется переходным процессом, возникающем в системе при нарушении ее равновесия любым возмущением. Основной динамической характеристикой системы регулирования является ее устойчивость или неустойчивость. Исследование замкнутых АСР на ...
... на основе правил Госгортехнадзора с учетом местных условий и особенностей оборудования. Котел должен быть оборудован необходимым количеством контрольно-измерительных приборов, автоматической системой регулирования важнейших параметров котла, защитными устройствами, блокировкой и сигнализацией. Режимы работы котла должны соответствовать режимной карте, в которой указываются рекомендуемые ...
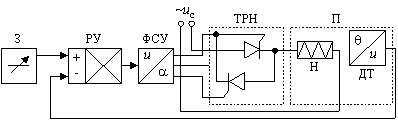
... , поддерживало температуру на нужном уровне. Установка требуемой температуры осуществляется с помощью задатчика (З). 1.2 Описание структурной схемы Рис. 2. Структурная схема автоматической системы регулирования температуры Входным сигналом системы является напряжение Uз, оно сравнивается с напряжением Uд ≈ Θ, которое действует на выходе датчика. Если Uз ≠ Uд, то ...
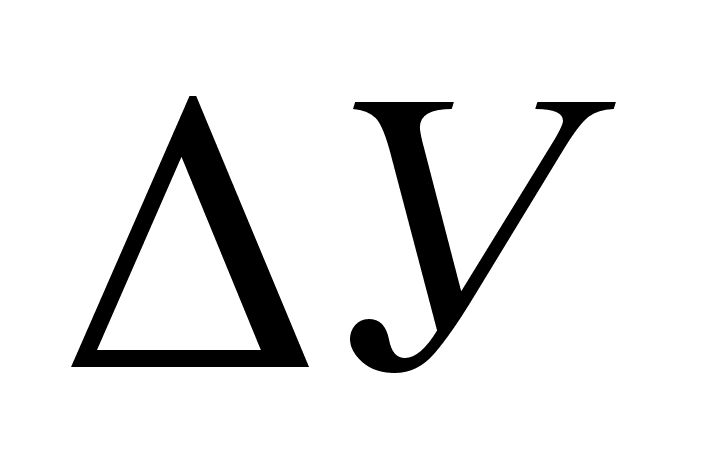
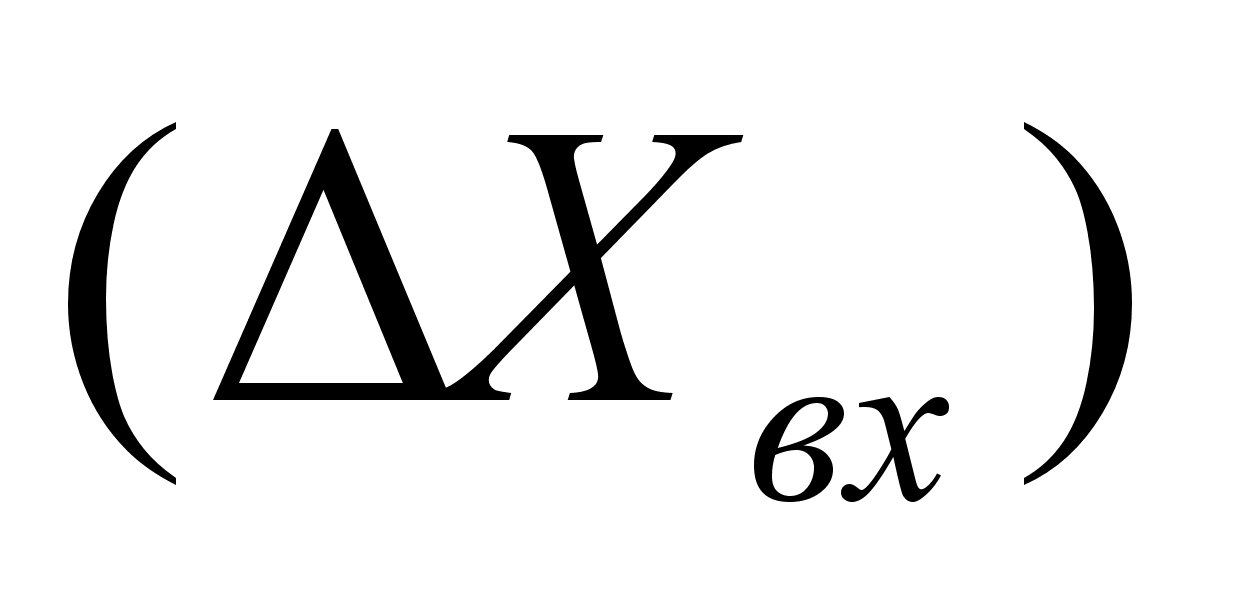
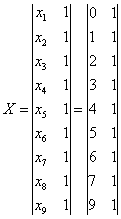
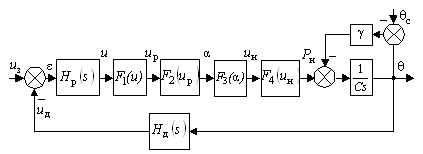
0 комментариев