Построение статической характеристики объекта
Аппроксимация полиномом второго порядка
Расчет коэффициентов передачи
Модель объекта первого порядка без запаздывания
Модель объекта первого порядка с запаздыванием
Построение математической модели
Выбор и расчет параметров настройки регуляторов
Расчет ПИ-регулятора
Обзор методов исследования на устойчивость
Проверка устойчивости по критерию Рауса
Проверка устойчивости по корням характеристического уравнения
Оценка качества функционирования АСР
Навигация
Модель объекта первого порядка с запаздыванием
Автоматическая система регулирования с П-регулятором
45149
знаков
18
таблиц
55
изображений
2.3 Модель объекта первого порядка с запаздыванием
Динамическая модель первого порядка с запаздыванием представляет собой неоднородное дифференциальное уравнение первого порядка:
(2.4)
где T - постоянная времени объекта;
k - коэффициент передачи при 50% номинального режима;
- время запаздывания.
Решением уравнения (2.1) будет экспоненциальная зависимость сигнала на выходе от времени:
(2.5)
где y0=0 - начальное состояние выхода объекта;
k.x=yуст.=10 - установившееся состояние выхода объекта.
Проведем преобразования, аналогичные модели без запаздывания
или запишем в виде системы :
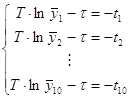(2.6)
где 
берется из табл. 7.
Так как 
, 
и 
, то все уравнения содержащие эти элементы в расчете участвовать не будут.
Решим систему (2.6) методом наименьших квадратов. Составим матрицы:
- искомых величин: 
- правой части системы: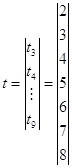 
- левой части системы: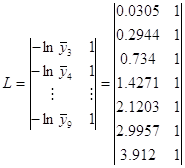 
- произведение 
- произведение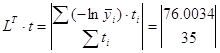 
Таким образом получили матричное уравнение:
Находим главный определитель:
Подставляя матрицу 
поочередно в первый и второй столбец матрицы 
, находим вспомогательные определители:
Находим постоянную времени и время задержки:
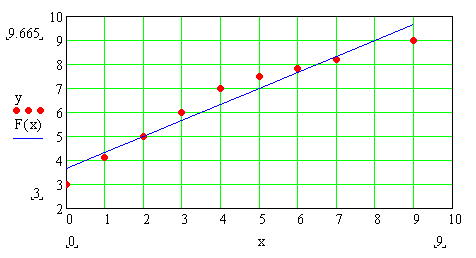
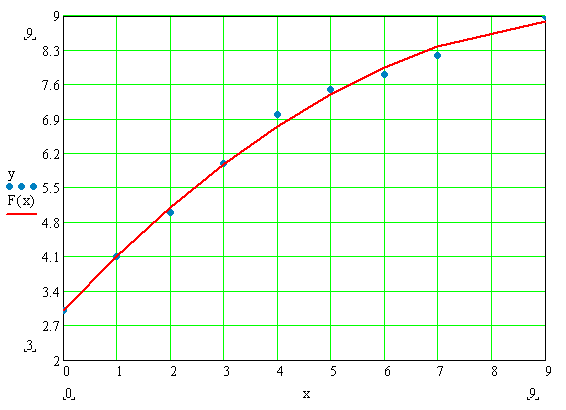
Таким образом динамическая характеристика первого порядка с запаздыванием будет иметь вид:
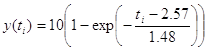
Вычислим аналитические значения функции, их отклонения от экспериментальных значений, а также квадраты отклонений, причем значения функции при 
учитывать не будем. Результаты сведем в табл. 8.
Таблица 8
Результаты расчета
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| yi | 0 | 0 | 0.5 | 0,71 | 0,8 | 0,91 | 0,98 | 0,99 | 0,995 | 1 |
| yiанал | 0 | 0 | 0.199 | 0.565 | 0.764 | 0.872 | 0.93 | 0.962 | 0.98 | 0.989 |
|
| 0 | 0 | 0.301 | 0.145 | 0.036 | 0.038 | 0.05 | 0.028 | 0.015 | 0.011 |
|
| 0 | 0 | 0.090493 | 0.020928 | 0.001291 | 0.001448 | 0.002451 | 0.000769 | 0.00024 | 0.000124 |
yi
Далее находим сумму квадратов отклонений:
.
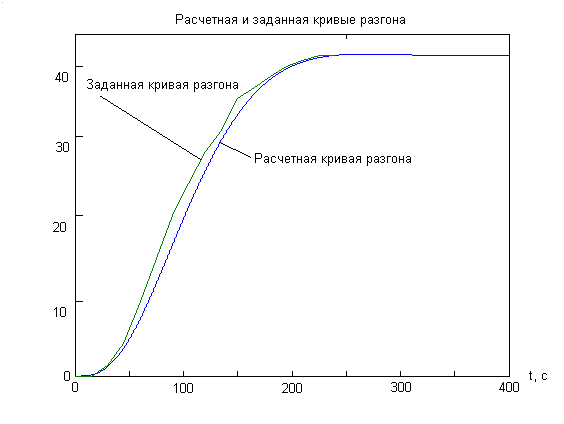
Так как сумма квадратов отклонений у модели с запаздыванием меньше, чем у модели без запаздывания, то ее использование позволяет более точно описывать протекание переходного процесса.
Расчет на ЭВМ моделей более высоких порядков показывает, что наименьшее значение суммы квадратов отклонений будет у модели второго порядка. Поэтому в дальнейших расчетах будем выполнять все действия именно для модели второго порядка.
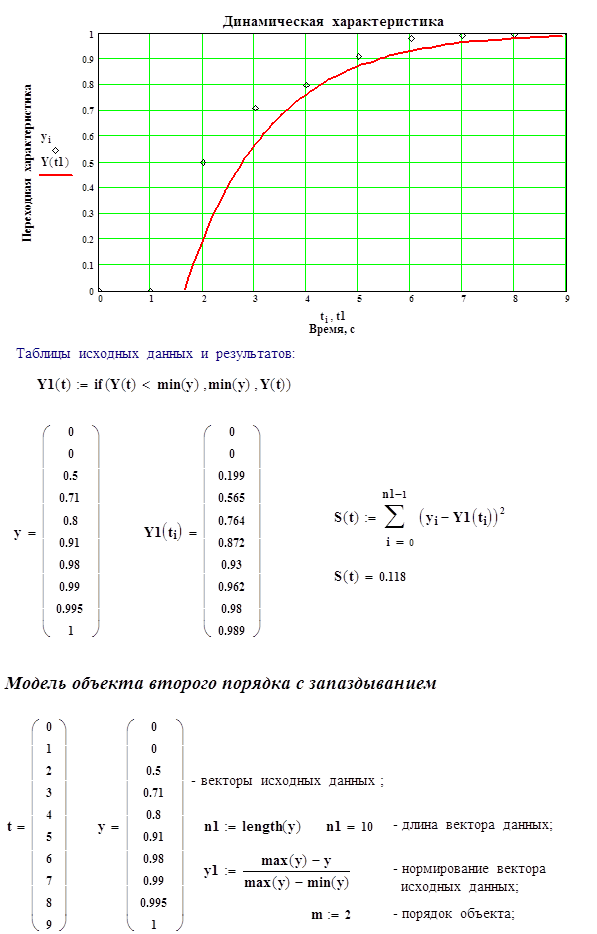
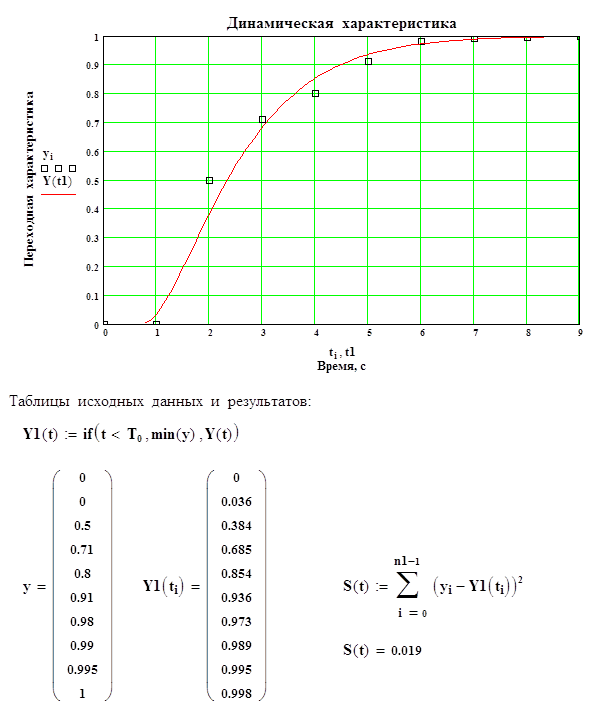
Ниже приведен проверочный расчет динамической модели объекта первого порядка с запаздыванием и модели второго порядка с запаздыванием на ЭВМ в системе MathCad.
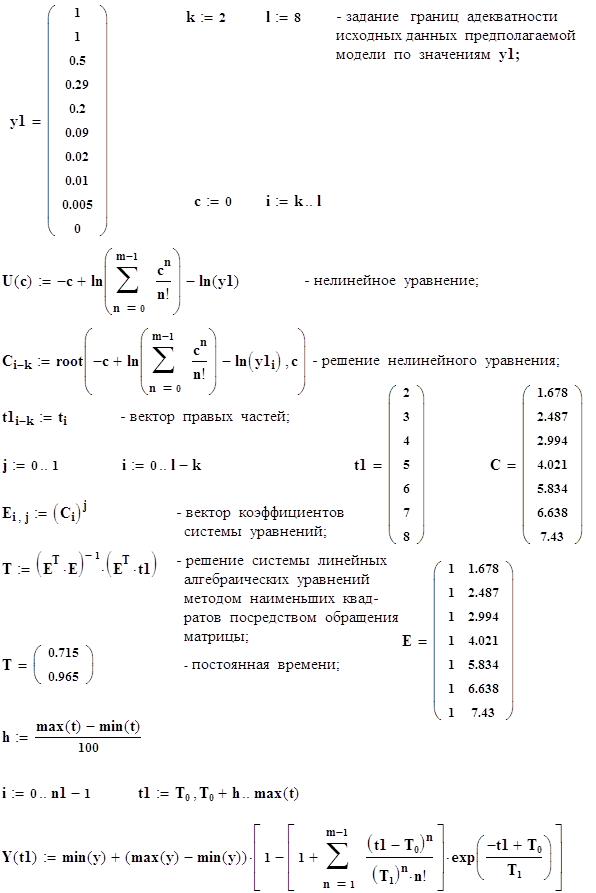
Похожие работы
... свойства объекта управления остаются, практически неизменными. Поэтому изучение характеристик объекта управления относятся к одной из основных задач теории автоматического управления и регулирования. В данной курсовой работе Я разрабатываю АСР для молотковой дробилки типа ДДМ-1, в соответствии с требованием данной технологии. Обеспечить оптимальный режим работы в выборе типа регулятора и закона ...
... ИССЛЕДОВАНИЕ НА УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 7.1 Постановка задачи Система автоматического регулирования как динамическая система, характеризуется переходным процессом, возникающем в системе при нарушении ее равновесия любым возмущением. Основной динамической характеристикой системы регулирования является ее устойчивость или неустойчивость. Исследование замкнутых АСР на ...
... на основе правил Госгортехнадзора с учетом местных условий и особенностей оборудования. Котел должен быть оборудован необходимым количеством контрольно-измерительных приборов, автоматической системой регулирования важнейших параметров котла, защитными устройствами, блокировкой и сигнализацией. Режимы работы котла должны соответствовать режимной карте, в которой указываются рекомендуемые ...
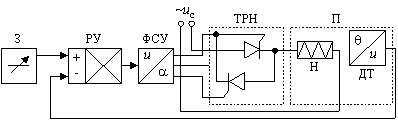
... , поддерживало температуру на нужном уровне. Установка требуемой температуры осуществляется с помощью задатчика (З). 1.2 Описание структурной схемы Рис. 2. Структурная схема автоматической системы регулирования температуры Входным сигналом системы является напряжение Uз, оно сравнивается с напряжением Uд ≈ Θ, которое действует на выходе датчика. Если Uз ≠ Uд, то ...
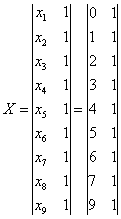
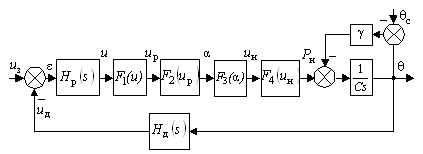
0 комментариев