Метод проектирования градиента

1.5.3 Метод проектирования градиента

Рассмотренные выше градиентные методы предполагали отыскание абсолютного минимума целевой функции Z. При наличии в математической модели нелинейных ограничений ищется уже не абсолютный, а относительный минимум целевой функции Z [1].

Рассмотрим один из методов отыскания относительного минимума целевой функции, получивший название метода проектирования градиента.

Для упрощения алгоритма допустим, что имеется одно ограничение в виде линейного неравенства

 (1.23)

При наличии указанного ограничения минимум целевой функции следует искать в области , расположенной по одну сторону от прямой например выше этой прямой (рис. 1.4).

Начало вычислительной процедуры такое же, как и в предыдущих методах:

в области  принимается исходное (нулевое) приближение х10, х20;

вычисляется значение целевой функции в этой точке Z0;

в соответствии с выражением (1.15) в этой точке вычисляется градиент целевой функции grad Z;

из исходной точки в направлении убывания целевой функции выполняется шаг.

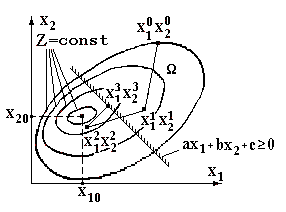
Рисунок 1.4 – Иллюстрация метода проектирования градиента

Выбор величины шага может осуществляться различным образом. Выберем шаг в соответствии с алгоритмом метода скорейшего спуска и получим первое приближение – точку с координатами х11, х21. Вычисляется значение целевой функции в этой точке Z1.

Необходимо проверить, принадлежит ли точка с координатами х11, х21 области  допустимых значений переменных. Для этого проверяется неравенство (1.23), в которое подставляются координаты х11, х21:

 (1.23)

Если это неравенство выполняется, вычислительный процесс продолжается.

Из точки с координатами х11, х21 выполняется следующий шаг. В результате этого шага имеем второе приближение – точку с координатами х12, х22. значение целевой функции в этой точке Z2.

Пусть для этой точки неравенство  не выполняется. Следовательно, точка с координатами х12, х22 вышла из области  и необходимо выполнить возврат в эту область.

Возврат в область  выполняется следующим образом. Из точки с координатами х12, х22 опускается перпендикуляр на прямую  т.е. конец вектора (х11, х21; х12, х22) проектируется на эту прямую. В результате получается новое приближение – точка с координатами х13, х23, которая принадлежит области . В этой точке вычисляется значение целевой функции Z3.

Дальнейший спуск к относительному минимуму целевой функции продолжается из точки х13, х23. на каждом шаге вычисляется значение целевой функции и проверяется принадлежность нового приближения к области . Вычислительный процесс заканчивается при выполнении условия (1.16).

1.6 Метод штрафных функций

Рассмотрим задачу поиска локального минимума критерия оптимальности W в области, ограниченной системой неравенств (3.16)-(3.17). Введение обобщенного критерия оптимальности по методу штрафных функций [3,5] производится с помощью непрерывной функции

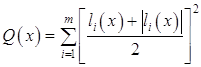. (1.24)

Обобщенным критерием оптимальности согласно методу штрафных функций является выражение

T=W+RQ(x),

где R - некоторое положительное число, называемое коэффициентом штрафа.

Рассматривается некоторая неограниченная, монотонно возрастающая последовательность {Rk}, k=1,2,... положительных чисел. Для первого элемента этой последовательности с помощью метода покоординатного спуска отыскивается локальный минимум функции T. Пусть этот минимум достигается при значениях (b*,R1).

Вектор (b*,R1) используется как начальное приближение для решения задачи поиска минимума функции T где R2>R1 и т.д. Таким образом, решается последовательность задач минимизации функций T(b*,Rk), k=1,2 ..., причем результат предыдущей оптимизации используется в качестве начального приближения для поиска последующей.

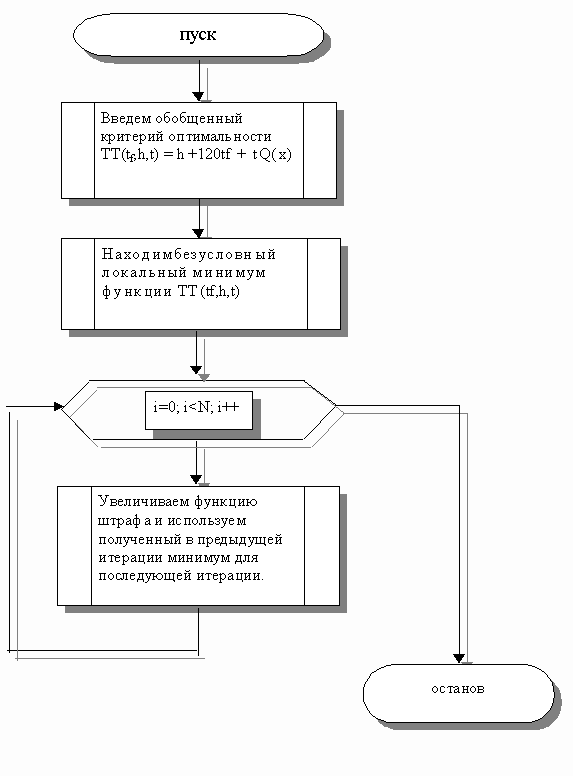
Рисунок 1.5 – Блок-схема метода штрафных функций