Навигация
Методы полиномиальной аппроксимации
1.7 Методы полиномиальной аппроксимации
Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать полиномом достаточно высокого порядка [6]. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома.
Рассмотрим следующие вопросы:
квадратичная аппроксимация;
кубическая интерполяция;
квадратичные функции.
1.7.1 Квадратичная аппроксимация
Используется несколько значений функции в определенных точках для аппроксимации функции обычным полиномом по крайней мере в небольшой области значений. Затем положение минимума функции аппроксимируется положением минимума полинома, поскольку последний вычислитель проще.
Простейший случай основан на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть по крайней мере квадратичной.
Если целевая функция W(x) в точках x1, x2, x3 принимает соответствующие значения W1, W2, W3, то можно определить коэффициенты aо, a1, a2 таким образом, что значения квадратичной функции
q(x) = ao + a1(x - x1) + a2(x - x1)(x - x2) (1.25)
совпадут со значением W(x) в трех указанных точках. Вычислим q(x) в трех указанных точках (см. табл.1.1).
Таблица 1.1 - Вычисление значений
|
|
|
|
|
|
|
|
|
|
|
|
1.7.1.1Метод Пауэлла
Если известны значения функции f(x) в трех разных точках α, β, γ равные соответственно fα, fβ, fγ, то функция f(x) может быть аппроксимирована квадратичной функцией
ö(x)=Ax2+Bx+C, (1.26)
где А, В и С определяются из уравнений
Aá2+Bá+C=fá,
Aâ2+Bâ+C=fâ,
Aã2+Bã+C=fã. (1.27)
После преобразований этих уравнений получаем
A=[(ã-â)fá+(á-ã)fâ+(â-á)fã] / D,
B=[(â2-ã2)fá+(ã2-á2)fâ+(á2-â2)fã] / D,
C=[âã(ã-â)fá+ãá(á-ã)fâ+áâ(â-ã)fã] / D, (1.28)
где D=(á-â)(â-ã)(ã-á)
Ясно, что φ(x) будет иметь минимум в точке
x=-B/2A,
если А>0. Следовательно, можно аппроксимировать точку минимума функции f(x) значением
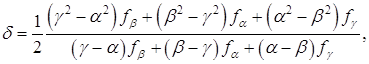 (1.29)
(1.29)
Этот метод может непосредственно применяться к функциям одной переменной. Он может быть очень полезен для выполнения линейного поиска в процедурах, описанных в теме №3. В этих процедурах требуется найти минимум функции f(x) в точках прямой x0+λd, где x0- заданная точка, а d определяет заданное направление. Значение функции f(x0+λd) на этой прямой является значениями функции одной переменной λ:
φλ = f(x0+λd). (1.30)
Идеи и результаты, изложенные выше, преобразуются в вычислительные процедуры, описанные далее. Предположим, что заданы унимодальная функция одной переменной f(x), начальная аппроксимация положения минимума и длинна шага D, является величиной того же порядка, что и расстояние от точки А до точки истинного минимума x*(условие, которое не всегда просто удовлетворить). Вычислительная процедура имеет следующие шаги:
Шаг 1. x2 = x1 + D x.
Шаг 2. Вычислить W(x1) и W(x2).
Шаг 3.
если W(x1) > W(x2), то x3 = x1 + 2 D x;
если W(x1)< W(x2), то x3 = x1 - D x;
W(x1) > W(x2),
Шаг 4. Вычислить W(x3) и найти
Wmin = min{ W(x1),W(x2), W(x3)},
Xmin = xi, соответствующая Wmin.
Шаг 5. По x1, x2, x3 вычислить x*, используя формулу для оценивания с помощью квадратической аппроксимации.
Шаг 6. Проверка окончания
если | Wmin - W(x*)| < W, то закончить поиск. В противном случае к шагу 7;
если | Xmin - x*| < x, то закончить поиск. В противном случае к шагу 7.
Шаг 7. Выбрать Xmin или x* и две точки по обе стороны от нее. Обозначить в естественном порядке и перейти к шагу 4.
Заметим, что если точка Е задана слишком малой, то á, â, ã, а также fá, fâ, fã будут очень близко друг к другу и значение d (1.29) может стать вообще недостижимыми. Чтобы преодолеть эту трудность, перепишем (1.29) для второй и последней интерполяции:
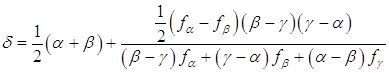 (1.31)
(1.31)
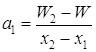
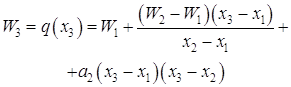
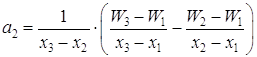
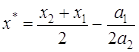
0 комментариев