Кубическая интерполяция

1.7.2 Кубическая интерполяция

Квадратичная интерполяция, которая рассматривалась в предыдущем разделе, называется методом Пауэлла и аппроксимирует функцию квадратным трехчленом. В этом разделе рассматривается метод Давидона [6,7], который гарантирует большую точность и аппроксимирует функцию кубическим полиномом.

Для кубической интерполяции в этом методе используются значения функции и ее производной, вычисленных в двух точках.

Рассмотрим задачу минимизации функции f(x) на прямой x0 + hd , то есть минимизацию функции

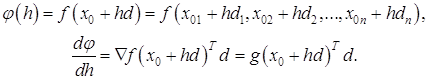 (1.32)

Предположим, что известные следующие значения:

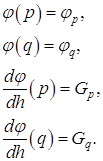 (1.33)

Эту информацию можно использовать для построения кубического полинома a+bh+ch2+dh3, который будет аппроксимировать функцию φ(h) Если p=0 , то уравнения, которые определяют a, b, c, d имеют вид :

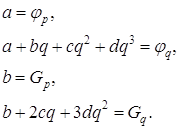 (1.34)

Следовательно, если r является точкой минимума кубического полинома,

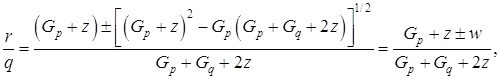 (1.35)

где

Одно из значений этого выражения является минимумом. Друга производная равна 2c +6dh.

Если мы выберем положительный знак, то при

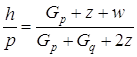
другая производная будет

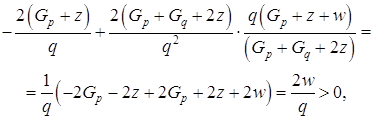 (1.36)

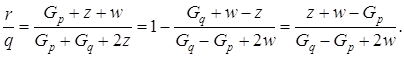 (1.37)

Выбор точки q зависит от нас. Если Gp >0 , то надо выбрать значение q положительным, то есть сделать шаг в направлении уменьшения функции φ(h) , в другом случае значения q надо выбирать отрицательным. Значение должно быть таким, чтобы интервал (0, ) включал в себя минимум. Это будет верным, если φq > φ p или Gp >0.

Если ни одно из этих условий не исполняется, то мы удваиваем значения q , повторяя это в случае необходимости, пока указанный интервал не будет содержать в себе минимум.

Давидон, Флетчер и Пауэлл предложили выбирать q следующим путем:

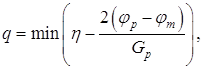 (1.38)

где φm - оценка самого малого значения истинного минимума φ(h),

h- константа, значение которой обычно берут 2 или 1.

1.7.3 Квадратичные функции

Квадратичная функция [7,8]

 (1.39)

где a - константа;

b - постоянный вектор;

G - положительно определенная симметричная матрица - имеет минимум в точке x* , где x* определяется следующим путем:

 (1.40)

откуда

Любую функцию можно аппроксимировать в окрестности точки x0 функцией

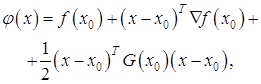 (1.41)

где G(x0) - матрица Гессе, вычисленная в точке x0.

Аппроксимацией минимума функции f(x) может быть минимум функции φ(x). Если последний находится в точке xm, то

 (1.42)

откуда

или

 (1.43)

Таким образом точкой xи следующей аппроксимации минимума будет:

 (1.44)

или

 (1.45)

где λи - длина шага, определяется одномерным поиском в направлении G-1(xи)g(xи).

1.8 Метод Нелдера-Мида

Метод Нелдера-Мида (поиск по деформируемому многограннику) является развитием симплексного метода Спендли, Хекста и Химсворта [7,8]. Множество (n+1)-й равноудаленной точки в n-мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. Следовательно, в двумерном пространстве симплексом является равносторонний треугольник, а в трехмерном пространстве правильный тетраэдр. Идея метода состоит в сравнении значений функции в (n+1) вершинах симплекса и перемещении в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенном первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самых эффективных, если n<=6.

В методе Спендли, Хекста и Химсворта симплекс перемещается с помощью трех основных операций: отражения, растяжения и сжатия. Смысл этих операций станет понятным при рассмотрении шагов процедуры.

Шаг 1. Найдем значения функции в вершинах симплекса:

f1=f( x1), f2=f(x2) ... fn+1=f(xn+1) (1.46)

Шаг 2. Найдем наибольшее значение функции fh, следующее за наибольшим значением функции fg , наименьшее значение функции fl и соответствующие им точки xh, xg и xl.

Шаг 3. Найдем центр тяжести всех точек, за исключением точки xh. Пусть центром тяжести будет

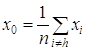 (1.47)

и вычислим f(x0)=f0.

Шаг 4. Удобнее всего начать перемещение от точки xh. Отразив точку xh относительно точки x0, получим точку xr и найдем f(xr) = fr.

Операция отражения иллюстрируется рис. 1.6.

Рисунок 1.6 – Операция отражения

Если α>0 - коэффициент отражения, то положение точки xr определяется следующим образом:

xr-x0=α (x0-xh), т.е.

xr=(1+α)x0 -αxh. (1.48)

Замечание.

α= |xr-x0| / |x0 –xh|.

Шаг 5. Сравним значения функций fr и fl.

Если fr<fl, то мы получили наименьшее значение функции. Направление из точки x0 в точку xr наиболее удобно для перемещения. Таким образом, мы производим растяжение в этом направлении и находим точку xe и значение функции fe=f(xe). Рисунок 1.7. иллюстрирует операцию растяжения симплекса. Коэффициент растяжения γ1 можно найти из следующих соотношений: xe-x0=γ (xr-x0), т.е.

xe=γxr+ (1-γ)x0. (1.49)

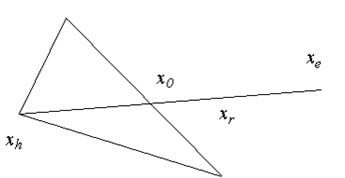
Рисунок 1.7 – Операция растяжения

Замечание

γ=|xe-x0| / |xr-x0|

Если fe<fl, то заменяем точку xh на точку xe и проверяем (n+1)-ую точку симплекса на сходимость к минимуму (см. шаг 8). Если сходимость достигнута, то процесс останавливается; в противном случае возвращаемся на шаг 2.

Если fe=fl , то отбрасываем точку xe. Очевидно, мы переместились слишком далеко от точки x0 к точке xr. Поэтому следует заменить точку xh на точку xr, в которой было получено улучшение (шаг 5, 1) проверить сходимость и, если она достигнута, вернуться на шаг 2.

Если fr>fl, но fr <=fgто xr является лучшей точкой по сравнению с другими двумя точками симплекса и мы заменяем точку xh на точку xr и, если сходимость не достигнута, возвращаемся на шаг 2, т.е. выполняем пункт 1,б, описанный выше.

Если fr>fl и fr>fgто перейдем на шаг 6.

Шаг 6. Сравним значения функций fr и fh.

Если fr>f h, то переходим непосредственно к шагу сжатия 6,2.

Если fr<fh, то заменяем точку xh на точку xr и значение функции fh на значение функции fr. Запоминаем значение fr>f g из шага 5,2, приведенного выше. Затем переходим на шаг 6,2.

В этом случае fr>f h, поэтому ясно, что мы переместились слишком далеко от точки xh к точке x0. Пытаемся исправить это, найдя точку xc (а затем fс) с помощью шага сжатия, показанного на рис. 1.8.

Если fr>f h, то сразу переходим к шагу сжатия и находим точку xc из соотношения

xc-x0=β(xh-x0), (1.50)

где β(0<b<1)- коэффициент сжатия. Тогда

xc=βxh+(1-β)x0. (1.51)

Если fr<f h, то сначала заменим точку xh на точку xr, а затем произведем сжатие. Тогда точку xc найдем из соотношения

xc-x0=β(xr-x0), т.е.

xc=βxr+(1-β)x0. (1.52)

Шаг 7. Сравниваем значения функций fc и fh.

Если fc<f h, то заменяем точку xh на точку xc, и если сходимость не достигнута ,то возвращаемся на шаг 2.

Если fc>f h, то очевидно, что все наши попытки найти значение меньшее fh закончились неудачей, поэтому мы переходим на шаг 8.

На этом шаге мы уменьшаем размерность симплекса делением пополам расстояния от каждой точки симплекса до xl-точки, определяющей наименьшее значение функции.

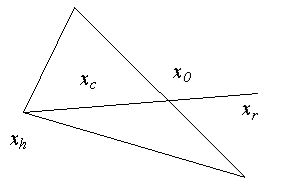
Рисунок 1.8 - Шаг сжатия для fr>fh

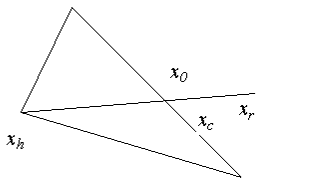
Рисунок 1.9 - Шаг сжатия для fr<fh

Таким образом, точка xi заменяется на точку

,

т.е. заменяем точку xi точкой .

Затем вычисляем fi для i=1,2,...,(n+1), проверяем сходимость и, если она достигнута, возвращаемся на шаг 2.

Шаг 9. Проверка сходимости основана на том, чтобы стандартное отклонение (n+1) -го значения функции было меньше некоторого заданного малого значения. В этом случае вычисляется

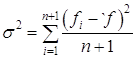, (1.53)

где .

Если σ<ε, то все значения функции очень близки друг к другу, и поэтому они, возможно, лежат вблизи точки минимума функции xl. Исходя из этого, такой критерий сходимости является разумным, хотя Бокс, Дэвис и Свенн предлагают то, что они считают более "безопасной" проверкой.

Коэффициенты αβγ в вышеприведенной процедуре являются соответственно коэффициентами отражения, сжатия и растяжения. Нелдер и Мид рекомендуют брать α=1, β=0.5 и γ=2. Рекомендация основана на результатах экспериментов с различными комбинациями значений. Эти значения параметров позволяют методу быть эффективным, но работать в различных сложных ситуациях.

Начальный симплекс выбирается на наше усмотрение. В данной программе точка x1 является начальной точкой, затем в программе формируются точки

x2=x1+ke1,

x3=x1+ke2,

xn+1=x1+ken, (1.54)

где k - произвольная длина шага,

ej - единичный вектор.