Навигация
1. График функции.
Функция ![]() называется линейной функцией. Для нахождения точек пересечения графика функции нужно решить два уравнения:
называется линейной функцией. Для нахождения точек пересечения графика функции нужно решить два уравнения:
![]()
Пример. Функция задана уравнением ![]() , найти точки пересечения с осями координат.
, найти точки пересечения с осями координат.
Решим два уравнения ![]()
Ответ: точки x =-2 и y = 4 являются точками пересечения с осями координат.
2. Квадратичная функция.
Функция вида ![]() называется квадратичной. Для нахождения точек пересечения графика с осями координат, нужно решить квадратное уравнение
называется квадратичной. Для нахождения точек пересечения графика с осями координат, нужно решить квадратное уравнение ![]()
Глава 3 Пределы
1. Предел функции
Пример. Найти предел функции
![]()
Поскольку икс стремится к двум, т.е. ![]() , то в числителе и знаменателе заменяем все иксы на 2, таким образом, получаем
, то в числителе и знаменателе заменяем все иксы на 2, таким образом, получаем
![]()
Ответ: ![]()
Рассмотрим случай, когда икс стремится к бесконечности. Пусть ![]()
Разделим числитель и знаменатель на высокую степень аргумента ![]() , получим
, получим
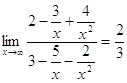
Ответ: ![]()
Пусть ![]() , разделим числитель и знаменатель на
, разделим числитель и знаменатель на ![]() , получим
, получим
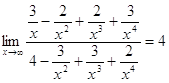
Ответ: 4
Найти предел ![]()
Отсюда ![]()
Ответ: 5
Глава 4 Производные
1. Обыкновенные производные
Пусть дана функция ![]() , требуется найти производную. Согласно выражению
, требуется найти производную. Согласно выражению ![]() , получим
, получим ![]() .
.
Пример: Найти производную функции
![]()
Отсюда
![]()
Ответ: ![]()
2. Производная функции одной переменной.
Функция одной переменной имеет вид ![]() , соответственно функция постоянно изменяется со скоростью, каждой границей изменения этой функции есть предел, который можно записать в виде
, соответственно функция постоянно изменяется со скоростью, каждой границей изменения этой функции есть предел, который можно записать в виде
![]() (21)
(21)
Функция ![]() называется дифференцируемой в точке x если предел (21)
называется дифференцируемой в точке x если предел (21)
существует.
3. Производные вида ![]()
В курсе дифференциальных уравнений часто можно видеть выражение ![]() .
.
Речь идет о частной производной, в этом выражении переменная x дифференцируется по переменной y. Рассмотрим выражение вида ![]() , в таком случае переменную x дифференцируют два раза по переменной y.
, в таком случае переменную x дифференцируют два раза по переменной y.
Пример. Найти производную ![]() , если
, если ![]()
![]()
Ответ: ![]()
ГЛАВА 5. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
1. Неопределенные и определенные интегралы.
Множество первообразных функции ![]() называется неопределенным интегралом. Такой неопределенный интеграл обозначается таким образом:
называется неопределенным интегралом. Такой неопределенный интеграл обозначается таким образом:
![]()
Где ![]() - подынтегральная функция,
- подынтегральная функция, ![]() - подынтегральное выражение,
- подынтегральное выражение, ![]() - постоянная интегрирования.
- постоянная интегрирования.
Пример: Вычислить интеграл ![]()
Находим первообразную для функции ![]() , получим
, получим ![]() , поэтому
, поэтому
![]()
Пример: Найти ![]()
Найдем первообразную для функции ![]() , получим
, получим ![]() , поэтому
, поэтому ![]()
Пример: Найти ![]()
Применяем метод непосредственного интегрирования, получим
![]()
Пример: Найти ![]()
Воспользуемся методом подстановки, получим
![]()
Тогда
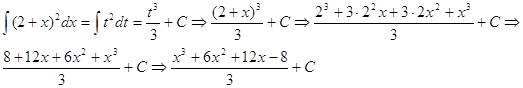
Пример: Найти ![]()
Воспользуемся методом интегрирования по частям, получим
![]()
Отсюда ![]()
Пример. Найти ![]()
Применим метод интегрирования по частям, получим
![]()
Отсюда
![]()
Рассмотрим интеграл вида 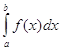 , такой интеграл называется определенным. Число а – называется нижним пределом, а число b – верхним пределом.
, такой интеграл называется определенным. Число а – называется нижним пределом, а число b – верхним пределом.
![]() Пример: Найти
Пример: Найти 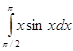
1. Находим неопределенный интеграл, методом интегрирования по частям,
![]()
Отсюда,
![]()
Тогда
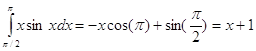
Пример: Найти 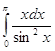
![]()
Отсюда,
![]()
Тогда
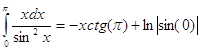
Похожие работы
... сделалась университетской наукой, была преподаваема в университетах и в большой и в большей или меньшей степени, разрабатывалась профессорами университетов. Здесь предлагается краткий очерк развития преподавания математики и самодеятельности русских ученых по университетам. Московский университет, старейший из русских, существуя почти 150 лет, насчитывает много поколений по математике. А.А. Барсов ...
... свойства параболы: парабола расположена в правой полуплоскости , проходит через начало координат О(0, 0) и имеет ось Ох своей осью симметрии. II. ПРИМЕНЕНИЕ АНАЛИТИЧЕСКОГО МЕТОДА К РЕШЕНИЮ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ. Мысль о возможности систематического применения метода координат в научных исследованиях зародилась несколько тысяч лет тому назад. Известно, например, что астрономы древнего мира, ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...
... . Некоторые из вариантов оказываются столь гармоничными и прекрасными, что очень сильно воздействовуют на эту специальную восприимчивость математика, и это позволит им перешагнуть порог сознания. Это подтверждается так же и тем фактом, что те интуитивные гипотезы, которые не выдерживают логической проверки, тем не менее в полной мере обладают гармонией. В этом случае часто говорят:"Жаль, что это ...

0 комментариев