Навигация
АЛГЕБРАИЧЕСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
1.7. АЛГЕБРАИЧЕСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
В этом разделе изучаются линии второго порядка, задаваемые в некоторой аффинной системе координат на плоскости алгебраическими уравнениями второй степени. Одна такая линия нам уже известна: это – окружность. Мы начнем с рассмотрения дальнейших конкретных примеров таких линий -эллипса, гиперболы и параболы.
Эти замечательные кривые были известны ещё древнегреческим математикам, начиная с IV в. до н.э. в связи со знаменитой задачей об удвоении куба, которую можно рассматривать как задачу о нахождении точки пересечения двух парабол х2 = у и у2 = 2х. В частности, Аристей в работе «О пространственных местах» уже рассматривал три различных типа конических сечений: эллипс, гиперболу и параболу. Основополагающий вклад в изучение этих линий внес Апполоний из Перги (около 260 – 177 гг. до н.э.). Его знаменитый трактат из восьми книг «О конических сечениях», из которого до нас дошли семь (известна реконструкция восьмой книги, предложенная современником И. Ньютона знаменитым астрономом Э. Галлеем) по своей фундаментальности сопоставим разве что с трактатом Евклида «Начала», написанном в III в. до н.э. Он установил многие важные свойства этих кривых, в частности, как канонических сечений, дал им современные названия «эллипс» - недостаток, «гипербола» - избыток (по отношению к некоторым свойствам параболы). Эта работа Аполлония по существу явилась идейным истоком аналитической геометрии. Декарт, когда в своей книге «Геометрия» (1637 г.) он использовал систему алгебраических обозначений, пришедшую с арабского востока (и которой мы пользуемся до сих пор!). Идею использовать алгебру при изучении геометрических фигур высказывал также другой современник Декарта Пьер Ферма. Именно он впервые установил, что уравнения первой степени задают прямые, а второй – конические сечения.
Определение. Эллипсом называется совокупность всех точек плоскости, сумма расстояний которых до двух данных точек этой плоскости (называемых фокусами эллипса), есть величина постоянная.
Пусть F1, F2 –данные точки и расстояние между ними ![]() . Введем на плоскости декартову систему координат, приняв за ось Ох прямую (F1F2), а за ось Оу – прямую, проходящую через середину О отрезка
. Введем на плоскости декартову систему координат, приняв за ось Ох прямую (F1F2), а за ось Оу – прямую, проходящую через середину О отрезка ![]() перпендикулярно оси Ох. Назовем эту систему координат канонической для рассматриваемого эллипса.
перпендикулярно оси Ох. Назовем эту систему координат канонической для рассматриваемого эллипса.
Теорема. В канонической системе координат уравнение Эллиса может быть записано в виде (оно называется каноническим уравнением эллипса):
![]() . (1)
. (1)
 Доказательство. В канонической системе координат имеем F1 (-с, 0), F2 (с, 0). Для составления уравнения эллипса возьмем на нем произвольную (текущую) точку М (х, у) и найдем условия её принадлежности к рассматриваемому эллипсу
Доказательство. В канонической системе координат имеем F1 (-с, 0), F2 (с, 0). Для составления уравнения эллипса возьмем на нем произвольную (текущую) точку М (х, у) и найдем условия её принадлежности к рассматриваемому эллипсу ![]() . По определению имеем:
. По определению имеем:
![]() .
.
По формуле расстояния между двумя точками имеем: ![]() . Преобразуем полученное уравнение:
. Преобразуем полученное уравнение:
![]() .
.
Возведем в квадрат обе чести:
![]() ,
,
![]() .
.
Возведем в квадрат еще раз: ![]() ,
,
![]() , (2)
, (2)
Заметим, что так как 2а – сема дли двух сторон треугольника F1М F2, а 2с – длина его третьей стороны, поэтому ![]() и значит
и значит ![]() . Обозначит тогда
. Обозначит тогда ![]() , (3).
, (3).
Тогда уравнение (2) принимает вид: ![]() , откуда поделив обе части на
, откуда поделив обе части на ![]() , приходим к требуемому уравнению (1).
, приходим к требуемому уравнению (1).
Параметрические уравнения эллипса в канонической системе координат имеют вид: ![]() . Действительно, подставляя эти выражения в каноническое уравнение эллипса (1), приходим к основному тригонометрическому тождеству:
. Действительно, подставляя эти выражения в каноническое уравнение эллипса (1), приходим к основному тригонометрическому тождеству: ![]() .
.
Определение. Гиперболой называется совокупность всех точек плоскости, разность расстояний которых до двух данных точек этой плоскости (называемых фокусами гиперболы) есть величина постоянная.
Как и для эллипса, вводим аналогичным образом для гиперболы каноническую систему координат.
Теорема. В канонической системе координат уравнение гиперболы может быть записано в следующем виде (оно называется каноническим уравнением гиперболы): ![]() , (4).
, (4).
Доказательство. Здесь условие принадлежности, текущей точки М к гиперболе ![]() , виду определения гиперболы, принимает вид:
, виду определения гиперболы, принимает вид:
![]()
т.е. ![]() . Преобразуя его совершенно подобным образом, как и в случае эллипса (дважды последовательно возводя в квадрат обе части уравнения), мы придем к тому же самому уравнению (2):
. Преобразуя его совершенно подобным образом, как и в случае эллипса (дважды последовательно возводя в квадрат обе части уравнения), мы придем к тому же самому уравнению (2): ![]() .
.
Заметим, что в данному случае 2а – разность длин двух сторон треугольника F1М F2, а 2с – длина его третьей стороны, поэтому в случае гиперболы ![]() и значит,
и значит, ![]() . Поэтому в этом случае обозначаем:
. Поэтому в этом случае обозначаем: ![]() или
или ![]() , (5).
, (5).
Тогда для гиперболы уравнение (2) принимает вид ![]() , откуда, поделив обе части на
, откуда, поделив обе части на ![]() , приходим к требуемому уравнению
, приходим к требуемому уравнению ![]() .
.
Параметрические уравнения гиперболы в канонической системе координат имеют вид: ![]() , где
, где ![]() - гиперболический косинус,
- гиперболический косинус, ![]() - гиперболический синус. Действительно, подставляя эти выражения в каноническое уравнение гиперболы (4), приходим к основному гиперболическому тождеству:
- гиперболический синус. Действительно, подставляя эти выражения в каноническое уравнение гиперболы (4), приходим к основному гиперболическому тождеству: ![]() .
.
Определение. Параболой называется совокупность всех точек, равноудаленных от данной точки этой плоскости (называемой фокусом параболы) и от данной прямой (называемой директрисой). При этом предполагается, что фокус не лежит на директрисе.
Каноническая система координат для параболы вводится следующим образом: её ось Ох проходит через середину О отрезка оси Ох, заключенного между F и d перпендикулярно оси Ох.
Теорема. В канонической системе координат уравнение параболы может быть записано в следующем виде: ![]() . (6)
. (6)
 Доказательство. Пусть
Доказательство. Пусть ![]() - расстояние от фокуса F до директрисы d (называется параметром параболы
- расстояние от фокуса F до директрисы d (называется параметром параболы ![]() ). Тогда
). Тогда ![]() , где
, где ![]() . Пусть М (х, у) – текущая точка параболы
. Пусть М (х, у) – текущая точка параболы ![]() . Найдем расстояния, участвующие в определении параболы:
. Найдем расстояния, участвующие в определении параболы:
![]() где
где ![]() . Тогда по определению параболы имеем:
. Тогда по определению параболы имеем:
![]()
По этому уравнению легко устанавливаются следующие свойства параболы: парабола расположена в правой полуплоскости ![]() , проходит через начало координат О(0, 0) и имеет ось Ох своей осью симметрии.
, проходит через начало координат О(0, 0) и имеет ось Ох своей осью симметрии.
II. ПРИМЕНЕНИЕ АНАЛИТИЧЕСКОГО МЕТОДА К РЕШЕНИЮ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ.
Мысль о возможности систематического применения метода координат в научных исследованиях зародилась несколько тысяч лет тому назад. Известно, например, что астрономы древнего мира, используя специальные системы координат на воображаемой небесной сфере, определяли положение наиболее ярких звёзд, составляли карты звёздного неба, вели отличавшиеся большой точностью наблюдения за перемещением Солнца, Луны и планет относительно неподвижных звёзд. В более позднюю эпоху широко развилось использование системы географических координат для составления карт земной поверхности и определения местонахождения корабля в открытом море. Однако до XVII века применение метода координат имело односторонний характер: им пользовались, по сути, только для указания положения определённого объекта — неподвижного (гора, мыс) или движущегося (корабль, планета). Новое, исключительно плодотворное применение получил метод координат в книге французского философа и математика Рене Декарта «Геометрия», изданной в 1637 году. Декарт выяснил важное значение понятия переменной величины. Занимаясь изучением наиболее употребительных линий, Декарт заметил, что координаты точки, перемещающейся по данной линии, связаны определённым уравнением, вполне характеризующим эту линию. Так был найден способ изучения линий по их уравнениям, положивший начало аналитической геометрии и способствовавший развитию других математических наук. «Поворотным пунктом в математике, — писал Энгельс, — была декартова переменная величина. Благодаря этому в математику вошли движение и диалектика и благодаря этому же стало немедленно необходимым дифференциальное и
интегральное исчисление». Математической основой аналитической геометрии является своеобразный способ определения геометрических фигур: фигура задаётся уравнением. Возможны два подхода к выяснению сущности этого способа. Рассматривая точку с переменными координатами х, у, связанными некоторым уравнением, мы замечаем, что она перемещается в плоскости с изменением её координат, но пробегаемый ею путь не будет произвольным, так как данное уравнение устанавливает зависимость между величинами х и у. Иными словами, уравнение играет роль как бы рельсов, направляющих движение точки по Возможно, однако, не связывать задание фигуры уравнением с представлением о движущейся точке, описывающей эту фигуру подобно трассирующей пуле, оставляющей светящийся след, или подобно перу сейсмографа, вычерчивающему линию, отображающую колебания земной коры. Можно рассматривать уравнение как средство для отбора точек, составляющих определяемую уравнением фигуру: отбираются те точки плоскости, координаты которых удовлетворяют данному уравнению.
Использование метода координат при решении планиметрических задач состоит из следующих этапов:
1) вводят удобным образом систему координат, чаще всего декартову;
2) условие задачи и её заключение переводят на соответствующий язык, записывая их в координатной форме;
3) доказывают или вычисляют требуемое с помощью соответствующего алгебраического аппарата;
4) полученный результат формулируют (интерпретируют) в терминах задачи.
Задача 1. Даны вершины треугольника А (5; -1), В(-1; 7), С (1; 2). Найти длину его внутренней биссектрисы, проведенной из вершины А.
Решение. Обозначим через М точку пересечения указанной биссектрисы со стороной ВС, через c и b — длины сторон АВ и АС. Как известно из элементарной геометрии, биссектриса, проведенная из какой-нибудь вершины треугольника, делит противолежащую этой вершине сторону на части, пропорциональные прилежащим сторонам. Таким образом, точка М делит отрезок ВС в отношении ![]() , где
, где
![]()
Находим длины сторон АВ и АС
![]() ,
, ![]() .
.
Следовательно, ![]() = 2. Находим координаты точки М:
= 2. Находим координаты точки М: ![]()
Получаем искомую длину биссектрисы ![]()
Задача 2. Докажите, что если диагонали трапеции равны, то трапеция равнобочная.
Решение. Введем декартову систему координат, начало которой поместим в середину нижнего основания, а ось Ох направим вдоль нижнего основания (рис.1). Тогда для координат вершины трапеции будем иметь:
А (-а, 0), D (а, 0), В (а, 1), С (с, 1)
![]()

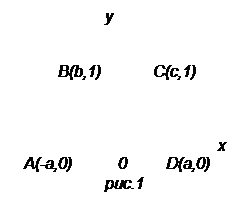 (считаем что единица масштаба по оси Оу равны высоте трапеции). По условию, АС = ВD, или в координатах:
(считаем что единица масштаба по оси Оу равны высоте трапеции). По условию, АС = ВD, или в координатах: ![]() . Отсюда (возведем это равенство квадрат):
. Отсюда (возведем это равенство квадрат):
![]() а2 + 2ас + с2 + 1 = а2 – 2аb + b2 + 1, или (с + b)(2а + с - b) = 0.
а2 + 2ас + с2 + 1 = а2 – 2аb + b2 + 1, или (с + b)(2а + с - b) = 0.
Второй сомножитель явно равен 0. Следовательно, b + с = 0, и значит,
b = - с и АВ = DC, т.е. трапеция равнобочная.
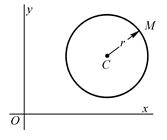 Задача 3. Дана декартова прямоугольная система координат. Вывести уравнение окружности, которая имеет центр
Задача 3. Дана декартова прямоугольная система координат. Вывести уравнение окружности, которая имеет центр ![]() и радиус, равный r (рис. 2).
и радиус, равный r (рис. 2).
![]() Решение. Обозначим, буквой М переменную точку, буквами х, у — ее координаты (т. е. текущие координаты). Данная окружность есть геометрическое место точек, каждая из которых отстоит от точки С на расстоянии r; таким образом, точка М находится на данной окружности в том и только в том случае, когда
Решение. Обозначим, буквой М переменную точку, буквами х, у — ее координаты (т. е. текущие координаты). Данная окружность есть геометрическое место точек, каждая из которых отстоит от точки С на расстоянии r; таким образом, точка М находится на данной окружности в том и только в том случае, когда
СМ = r. (1)
По формуле имеем ![]() . Заменяя этим выражением величину СМ в равенстве (1), получаем
. Заменяя этим выражением величину СМ в равенстве (1), получаем
![]() .
.
Мы нашли уравнение, которое связывает величины х, у и которому удовлетворяют координаты тех и только тех точек, что лежат на данной окружности. Это и есть, следовательно, искомое уравнение. Задача решена.
Задача 4. Даны уравнения двух окружностей ![]() и
и ![]() . Найти точки их пересечения.
. Найти точки их пересечения.
Решение. Раскрывая скобки и перенося все члены в левую сторону, можем записать данные уравнения в виде:
![]() ,
, ![]() . (1)
. (1)
Вычтем из первого уравнения второе; получим: ![]() или
или ![]() . Объединяя это уравнение с первым из данных, составим систему
. Объединяя это уравнение с первым из данных, составим систему
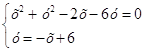 (2)
(2)
Система (2) равносильна системе (1). Поэтому задача сводится к решению
этой системы. Подставим в первое из уравнений (2) ![]() , найдем:
, найдем: ![]() , или
, или ![]() . Отсюда
. Отсюда ![]() , т.е.
, т.е. ![]() ,
, ![]() . По найденным значениям х определим соответствующие значения у из уравнения
. По найденным значениям х определим соответствующие значения у из уравнения ![]() ; при
; при ![]() получаем
получаем ![]() , при
, при ![]() имеем
имеем ![]() . Таким образом, искомыми являются точки (1; 5) и (3; 3).
. Таким образом, искомыми являются точки (1; 5) и (3; 3).
Задача 5. Дан треугольник АВС. Проведены медианы СD и прямая l, пересекающая лучи СА, СВ, СD соответственно в точках М, N, K, таких, что ![]() ,
, ![]() ,
, ![]() .
.
Доказать, что ![]() .
.
Решение. Примем вершину С треугольника АВС за начало аффинной системы координат, а СА(а) и СВ(а) – за базисные векторы. В таком случае точки будут иметь координаты: А (1, 0); В (0, 1), ![]() , М (m, 0), N (0, n). Так как СК(а) = kCD(а) и
, М (m, 0), N (0, n). Так как СК(а) = kCD(а) и ![]() , то
, то ![]() .
.
Координаты точки К удовлетворяют уравнению прямой MN:
![]()
Подставив координаты точки К в это уравнение, получим:
![]()
Задача 6. Даны две прямые 2х + 3у - 5 = 0, 7х + 15у + 1 = 0, пересекающиеся в точке S. Составить уравнение прямой, которая проходит через точку S и перпендикулярна к прямой 12х - 5у - 1 = 0.
Решение. Прежде всего, проверим утверждение условия задачи: данные прямые действительно пересекаются, так как ![]() . Далее составим уравнение пучка прямых с центром S:
. Далее составим уравнение пучка прямых с центром S:
![]() (1)
(1)
Чтобы выделить в этом пучке искомую прямую, вычислим согласно условию перпендикулярности этой прямой к прямой 12х - 5у - 1 = 0. Представив уравнение (1) в виде
![]() (2)
(2)
находим угловой коэффициент искомой прямой:
![]() .
.
Данная прямая имеет угловой коэффициент
![]() .
.
По условию перпендикулярности ![]() , т.е.
, т.е.
![]()
Отсюда ![]() . Подставляя
. Подставляя ![]() в уравнение (2), получаем -5x-12у-6=0 или 5х+12у+6 = 0.
в уравнение (2), получаем -5x-12у-6=0 или 5х+12у+6 = 0.
Задача решена.
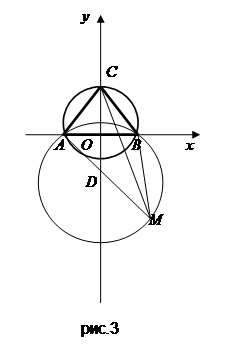 Задача7. Даны равносторонний треугольник АВС и окружность, проходящая через вершины А и В, центр которой симметричен вершине С относительно прямой АВ. Доказать, что если М – произвольная точка окружности, то из отрезков МА, МВ, МС можно составить прямоугольный треугольник (который вырождается, если М = А или М = В).
Задача7. Даны равносторонний треугольник АВС и окружность, проходящая через вершины А и В, центр которой симметричен вершине С относительно прямой АВ. Доказать, что если М – произвольная точка окружности, то из отрезков МА, МВ, МС можно составить прямоугольный треугольник (который вырождается, если М = А или М = В).
Решение. Введем на плоскости прямоугольную систему координат. За начало координат возьмем середину О отрезка АВ, точку В примем за единичную точку оси абсцисс (рис.7). Тогда |ОА| = |ОВ| = 1, |ВС| = 2 и |ОС| = ![]() . Следовательно, данные точки получают координаты: А (-1,0), В (1, 0), С (0,
. Следовательно, данные точки получают координаты: А (-1,0), В (1, 0), С (0, ![]() ), D (0,
), D (0, ![]() ). Уравнение окружности с центром D радиуса |АD| имеет вид
). Уравнение окружности с центром D радиуса |АD| имеет вид ![]() . Пусть
. Пусть ![]() - некоторая точка этой окружности. Требуется доказать, что |МА|2 + |МВ|2 = |МС|2.По формуле расстояния между двумя точками имеем:
- некоторая точка этой окружности. Требуется доказать, что |МА|2 + |МВ|2 = |МС|2.По формуле расстояния между двумя точками имеем:![]() ;
;![]() ;
; ![]() .
.
Отсюда ![]() .
.
Учитывая, что координаты точки ![]() удовлетворяют уравнению окружности, т.е.
удовлетворяют уравнению окружности, т.е. ![]() , получаем:
, получаем:
|МА|2 + |МВ|2 = |МС|2.
ЗАКЛЮЧЕНИЕ
Алгебра и геометрия, которые сейчас большинство школьников воспринимают как совершенно разные науки, на самом деле очень близки. С помощью метода координат можно было бы изложить весь школьный курс геометрии без единого чертежа, используя только числа и алгебраические операции. Курс планиметрии начинался бы словами: «Назовем точкой пару чисел (х, у) ...». Далее можно было бы определить окружность как совокупность точек, удовлетворяющих уравнению вида
(х — а)2 + (у — b)2 = R2. Прямой линией называлась бы совокупность точек, удовлетворяющих уравнению ах + by + с = 0. Многие другие фигуры можно было бы также охарактеризовать системами уравнений и неравенств. Все геометрические теоремы превратились бы при этом в некоторые алгебраические соотношения. Установление связи между алгеброй, с одной стороны, и геометрией, с другой, было, по существу, революцией в математике. Оно восстановило математику как единую науку, в которой нет «китайской стены» между отдельными ее частями. Создателем метода координат считают французского философа и математика Рене Декарта (1596—1650). В последней части большого философского трактата Декарта, вышедшей в 1637 году, давались описание метода координат и его применение к решению геометрических задач. Развитие идей Декарта привело к возникновению особой ветви математики, которую теперь называют аналитической геометрией.
Само это название выражает основную идею теории. Аналитическая геометрия — это та часть математики, которая решает геометрические задачи аналитическими (т. е. алгебраическими) средствами. Хотя аналитическая геометрия является сейчас уже вполне развившимся и законченным разделом математики, идеи, лежащие в ее основе, породили новые отрасли математики. Возникла и развивается алгебраическая геометрия, которая изучает свойства линий и поверхностей, заданных алгебраическими уравнениями. Эту часть математики никак нельзя считать законченной. Как раз в последние годы в ней получены новые фундаментальные результаты, оказавшие большое влияние и на другие разделы математики.
Характерной особенностью метода координат является определение геометрических фигур уравнениями, что позволяет производить геометрические исследования и решать геометрические задачи средствами алгебры. Придавая геометрическим исследованиям алгебраический характер, метод координат переносит в геометрию наиболее важную особенность алгебры — единообразие способов решения задач. Если в арифметике и элементарной геометрии приходится, как правило, искать для каждой задачи особый путь решения, то в алгебре и аналитической геометрии решения проводятся по общему для всех задач плану, легко приспособляемому к любой задаче. Можно сказать, что аналитическая геометрия занимает такое же положение по отношению к элементарной геометрии, какое алгебра занимает относительно арифметики. Перенесение в геометрию свойственных алгебре и поэтому обладающих большой общностью способов решения задач составляет главную ценность метода координат. Приёмы элементарной геометрии в отдельных случаях позволяют находить изящные решения, более простые, чем получаемые методом координат.
Другое достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций. При практическом применении понятия координат координаты предмета, рассматриваемого условно как точка, могут быть определены лишь приближённо. Задание координат предмета означает, что точка, определяемая этими координатами, либо является одной из точек этого предмета либо достаточно близка к нему.
Метод координат важен также и тем, что он позволяет применять современные вычислительные машины к решению геометрических задач, к исследованию любых геометрических объектов и соотношений.
Список используемой литературы.
1. Габович И., Горнштейн П. Вооружившись методом координат// Квант. – 1978. - №11. – с. 42 – 47.
2. Гельфанд И.М. Глаголева Е.Г., Нириллов А.А. Метод координат. – М.: Наука, 1973.
3. Готман Э.Г. Скопец З.А., Решение геометрических задач аналитическим методом. – М.: Просвещение, 1979.
4. Ефимов Н. В. Краткий курс аналитической геометрии: Учебн. пособие. — М.: ФИЗМАТЛИТ, 2005.
5. Игошин В.И. Аналитическая геометрия. – Саратов: Наука, 2007.
6. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. — М.: Наука, 1999.
7. Погорелов А.В. Аналитическая геометрия. – М.: Наука, 1968.
8. Смогоржевский А. С. Метод координат. – М., Государственное издательство технико-теоретической литературы, 1952.
Похожие работы
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4|MN|2.Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.Так как m = и n = , то |AB|2+|BC|2+|CD|2+|DA|2 |AC|2+|BD|2+4|MN|2 .Равенство доказано.Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, ...
... , основанной на поглощении атомами рентгеновского излучения. Ультрафиолетовая спектрофотометрия — наиболее простой и широко применяемый в фармации абсорбционный метод анализа. Его используют на всех этапах фармацевтического анализа лекарственных препаратов (испытания подлинности, чистоты, количественное определение). Разработано большое число способов качественного и количественного анализа ...
... координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений. Можно выделить следующие цели изучения метода координат в школьном курсе геометрии: - дать учащимся эффективный метод решения задач и доказательства ряда теорем; - показать на основе этого метода тесную связь алгебры и геометрии; - способствовать ...







0 комментариев