Навигация
Примеры: в нижеследующих примерах приведены образцы исследования элементарных функций, заданных формулами, содержащими обратные тригонометрические функции.
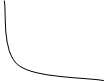
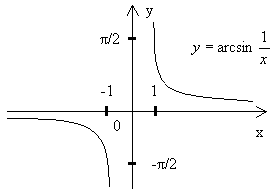
Пример №1. Исследовать функции arcsin(1/x) и arccos(1/y) и построить их графики.
Решение: Рассмотрим 1-ю функцию
|
|
![]()
|
|
![]()
![]() | x | ≥ 1 ,
| x | ≥ 1 ,
( - ∞ ; -1 ] U [ 1; + ∞ )
| ||||||
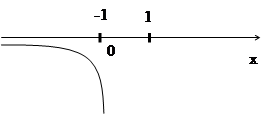 | ||||||
| ||||||
Функция нечетная
( f(x) убывает на пр. [0;1] , f(y) убывает на пр. [0;π/2] )
|
|

Д(f): ( - ∞ ; -1 ] U [ 1; + ∞ )
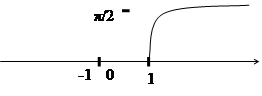 | |||
![]() Пример №2. Исследовать функцию y=arccos(x2).
Пример №2. Исследовать функцию y=arccos(x2).
|
![]() Д(f): [-1;1]
Д(f): [-1;1]
Четная
f(x) убывает на пр. [0;1]
![]()
![]()
|
|
|
| ||||
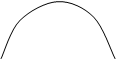
![]() Пример №3. Исследовать функцию y=arccos2(x).
Пример №3. Исследовать функцию y=arccos2(x).
 Решение: Пусть z = arccos(x), тогда y = z2
Решение: Пусть z = arccos(x), тогда y = z2
f(z) убывает на пр. [-1;1] от π до 0.
![]() f(y) убывает на пр. [-1;1] от π2 до 0.
f(y) убывает на пр. [-1;1] от π2 до 0.
![]()
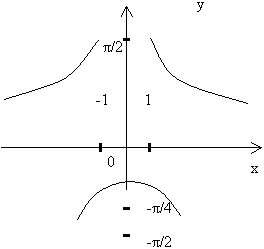
Пример №4. Исследовать функцию y=arctg(1/(x2-1))
Решение:
Д(f): ( - ∞ ; -1 ) U ( -1; 1 ) U ( 1; +∞ )
Т.к. функция четная, то достаточно исследовать функцию на двух промежутках:
|
![]()
|
| 0 | < x < | 1 | < x < | +∞ | ||||
| -1 | ↘ | + ∞ - ∞ | ↘ | 0 | ||||
|
| - π/4 | ↘ | π/2 - π/2 | ↘ | 0 |
|
|
Тригонометрические операции над аркфункциями
Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна через другую, поэтому в результате выполнения какой-либо тригонометрической операции над любой из аркфункций получается алгебраическое выражение.
В силу определения аркфункций:
sin(arcsin(x)) = x , cos(arccos(x)) = x
(справедливо только для x є [-1;1] )
tg(arctg(x)) = x , ctg(arcctg(x)) = x
(справедливо при любых x )
Графическое различие между функциями, заданными формулами:
y=x и y=sin(arcsin(x))
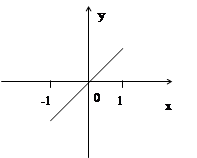 | |||
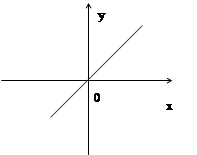 | |||
Сводка формул, получающихся в результате выполнения простейших тригонометрических операций над аркфункциями.
| Аргумент функция | arcsin(x) | arccos(x) | arctg(x) | arcctg(x) |
| sin | sin(arcsin(x))=x |
|
|
|
| cos |
| x |
|
|
| tg |
|
| x | 1 / x |
| ctg |
|
| 1 / x | x |
Справедливость всех этих формул может быть установлена при помощи рассуждений, приведенных ниже:
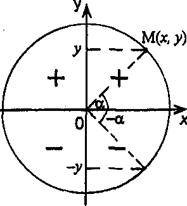
1. Т.к. cos2x + sin2x = 1 и φ = arcsin(x)
![]()
![]()
Перед радикалом ![]() следует взять знак “+”, т.к. дуга
следует взять знак “+”, т.к. дуга ![]() принадлежит правой полуокружности (замкнутой)
принадлежит правой полуокружности (замкнутой) ![]() , на которой косинус неотрицательный.
, на которой косинус неотрицательный.
Значит, имеем
![]()
2. Из тождества ![]() следует:
следует:
![]()
Похожие работы
... по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (4). Приняв во внимание равенство получим: Выполнение обратных тригонометрических операций над тригонометрическими функциями. При преобразовании выражений вида следует принимать во внимание в какой четверти находится аргумент х и в каком промежутке находится значение ...
... . Частные случаи тригонометрических уравнений Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями. Тригонометрические уравнения Аксиомы стереометрии и следствия из них Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых ...


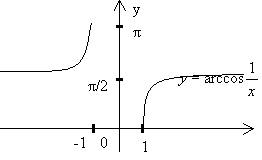
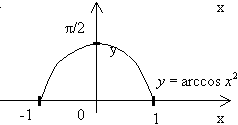
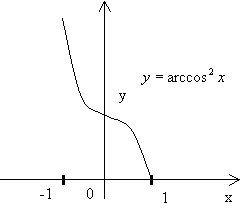
0 комментариев