Навигация
Выражение арктангенса через арккосинус. Из соотношения
6. Выражение арктангенса через арккосинус. Из соотношения
![]() при
при ![]() имеем:
имеем:
![]()
Если же х<0, то
![]()
Итак,
![]()
![]()
![]() , если
, если ![]() (6)
(6)
![]() , если
, если ![]()
7. Выражение арккосинуса через арктангенс. Если ![]() , то
, то ![]()
При
![]() имеем:
имеем:
![]()
Итак,
![]()
![]()
![]() , если
, если ![]() (7)
(7)
![]() , если
, если ![]()
8. Выражение арктангенса через арккотангенс.
![]()
![]()
![]() , если х>0 (8)
, если х>0 (8)
![]() ,если x<0
,если x<0
При x>0 равенство (8) легко установить; если же x<0, то
![]() .
.
9. Выражение арксинуса через арккотангенс.
![]()
![]()
![]() , если
, если ![]() (9)
(9)
![]() , если
, если ![]()
10. Выражение арккотангенса через арксинус.
![]()
![]()
![]() , если 0<x (10)
, если 0<x (10)
![]() , если х<0
, если х<0
11. Выражение арккотангенса через арктангенс.
![]()
![]()
![]() , если x>0 (11)
, если x>0 (11)
![]() , если x<0
, если x<0
Примеры:
Пример №1. Исследовать функцию ![]()
Решение. Эта функция определена для всех значений х, за исключением значения х=0 (при х=0) второе слагаемое теряет смысл). Воспользовавшись формулой (8) получим:
|
![]()
![]() y= 0 , если x>0
y= 0 , если x>0
-π , если x<0
![]()
![]() На чертеже изображен график
На чертеже изображен график
данной функции
![]()
Пример №2. Исследовать функцию ![]()
Решение: Первое слагаемое определено для значений ![]() , второе – для тех же значений аргумента. Преобразим первое слагаемое по формуле (4).
, второе – для тех же значений аргумента. Преобразим первое слагаемое по формуле (4).
Т.к. ![]() , то получаем
, то получаем
![]() ,
,
откуда:
![]() на сегменте [0;1]
на сегменте [0;1]
Пример №3. Исследовать функцию ![]()
Решение: Выражения, стоящие под знаками аркфункций не превосходят по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (4).
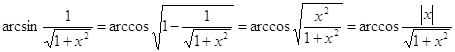
Приняв во внимание равенство
![]()
![]()
![]() , если
, если ![]()
![]() , если
, если ![]()
получим:
![]() y = 0 , если
y = 0 , если ![]()
![]() , если
, если ![]()
Выполнение обратных тригонометрических операций над тригонометрическими функциями.
При преобразовании выражений вида
![]()
следует принимать во внимание в какой четверти находится аргумент х и в каком промежутке находится значение данной аркфункции. Рассмотрим, например, первое из данных выражений:
![]()
Согласно определению арксинуса, y – есть дуга правой полуокружности (замкнутая), синус которой равен sin x;
![]() и
и ![]()
Областью определения функции ![]() служит интервал
служит интервал ![]() , так как при всех действительных значениях х значение промежуточного аргумента
, так как при всех действительных значениях х значение промежуточного аргумента ![]() содержится на сегменте
содержится на сегменте ![]() . При произвольном действительном х значение y (в общем случае) отлично от значения х.
. При произвольном действительном х значение y (в общем случае) отлично от значения х.
Так, например, при х=π/6 имеем:
![]()
но при х=5π/6
![]()
В силу периодичности синуса функция arcsin x также является периодической с периодом 2π, поэтому достаточно исследовать ее на сегменте [-π/2; 3π/2] величиной 2π.
Если значение х принадлежит сегменту [-π/2; π/2] то y=x, на этом сегменте график функции совпадает с биссектрисой координатного угла.
Если значение х принадлежит сегменту [π/2; 3π/2], то в этом случае дуга π-х принадлежит сегменту [-π/2; π/2]; и, так как
![]() , то имеем y=π-х;
, то имеем y=π-х;
в этом промежутке график функции совпадает с прямой линией y=π-х. Если значение х принадлежит сегменту [3π/2; 5π/2], то, пользуясь периодичностью или путем непосредственной проверки, получим:
y=х-2π
Если значение х принадлежит сегменту [-3π/2; -π/2], то
y=-π-х
Если значение х принадлежит сегменту [-5π/2; -3π/2], то
y=х+2π
Вообще, если ![]() , то
, то
y=х-2πk
и если ![]() , то
, то
y=(π-х)+2πk
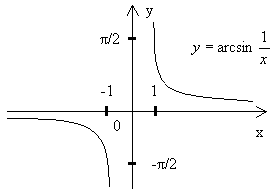
График функции ![]() представлен на рисунке. Это ломаная линия с бесконечным множеством прямолинейных звеньев.
представлен на рисунке. Это ломаная линия с бесконечным множеством прямолинейных звеньев.

Рассмотрим функцию ![]()
Согласно определению арккосинуса, имеем:
cos y = cos x, где ![]()
Областью определения данной функции является множество всех действительных чисел; функция периодическая, с периодом, равным 2π. Если значение Х принадлежит сегменту [0; π], то y = x. Если х принадлежит сегменту [π; 2π], то дуга 2π-х принадлежит сегменту [0; π] и ![]() , поэтому:
, поэтому:
![]()
Следовательно, на сегменте [π; 2π] имеем y = 2π - x
Если х принадлежит сегменту [2π; 3π], то y = x - 2π
Если х принадлежит сегменту [3π; 4π], то y = 4π – x
Вообще, если ![]() , то y = x - 2πk
, то y = x - 2πk
Если же ![]() , то y = -x + πk
, то y = -x + πk
Графиком функции ![]() является ломаная линия
является ломаная линия
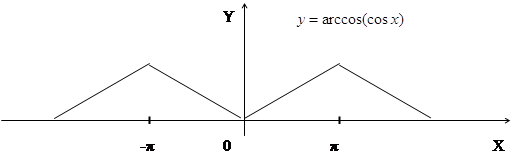
Формулы сложения
Формулы сложения дают выражения для суммы или разности двух (или нескольких) аркфункций через какую-либо данную аркфункцию. Пусть дана сумма аркфункций; над этой суммой можно выполнить любую тригонометрическую операцию. (....) В соответствии с этим дуга-функция может быть выражена посредством любой данной аркфункции. Однако в различных случаях (при одних и тех же аркфункциях) могут получаться различные формулы, в зависимости от промежутка, в котором берется значение рассматриваемой аркфункции.
Сказанное пояснено ниже на числовых примерах.
Примеры.
Пример №1. Преобразовать в арксинус сумму
![]()
Решение: эта сумма является суммой двух дуг α и β, где
![]() ;
; ![]()
В данном случае ![]() (т.к.
(т.к. ![]() , а следовательно,
, а следовательно, ![]() ), а также
), а также ![]() , поэтому
, поэтому ![]() .
.
Вычислив синус дуги γ, получим:
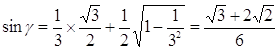
Т.к. сумма γ заключена на сегменте [-π/2; π/2], то
![]()
Пример №2. Представить дугу γ, рассмотренную в предыдущем примере, в виде арктангенса. Имеем:
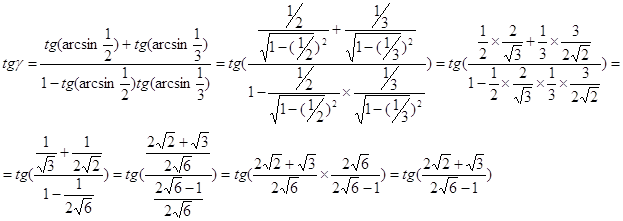
Откуда
![]()
Пример №3. Представить посредством арктангенса сумму ![]()
Решение: в данном случае (в отличие от предыдущего) дуга γ оканчивается во второй четверти, т.к. ![]() , а
, а ![]() . Вычисляем
. Вычисляем ![]()
В рассматриваемом примере ![]() , так как дуги γ и
, так как дуги γ и ![]() заключены в различных интервалах,
заключены в различных интервалах,
![]() , а
, а ![]()
В данном случае ![]()
Пример №4. Представить дугу γ, рассмотренную в предыдущем примере, в виде арккосинуса.
Решение: имеем
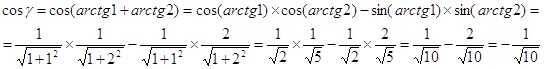
Обе дуги γ и ![]() расположены в верхней полуокружности и имеют одинаковый косинус, следовательно, эти дуги равны:
расположены в верхней полуокружности и имеют одинаковый косинус, следовательно, эти дуги равны: ![]()
Так как суммы и разности любых аркфункций можно выражать при помощи произвольных аркфункций, то можно получать самые разнообразные формулы сложения. Однако все эти формулы выводятся при помощи однотипных рассуждений. Ниже в качестве примеров даются некоторые из формул сложения, по этим образцам можно получить аналогичные формулы в различных прочих случаях.
Формулы сложения аркфункций от положительных аргументов.
Пусть α и β – две дуги, заключенные в промежутке от 0 до π/2 (первая четверть):
![]() , и
, и ![]()
Сумма α + β заключена в верхней полуокружности ![]() , следовательно, ее можно представить в виде аркфункции, значение которой выбирается в том же интервале, т.е. в виде арккосинуса, а также в виде арккотангенса:
, следовательно, ее можно представить в виде аркфункции, значение которой выбирается в том же интервале, т.е. в виде арккосинуса, а также в виде арккотангенса:
![]() ;
;
![]()
Разность α – β заключена в правой полуокружности: ![]()
Следовательно, она может быть представлена в виде арксинуса, а также в виде арктангенса:
![]() ;
;
![]()
Так как значение всякой аркфункции от положительного аргумента заключено в интервале (0; π/2) то сумму двух аркфункций от положительных аргументов можно представить в виде арккосинуса, а также в виде арккотангенса, а разность двух аркфункций от положительных аргументов можно представить в виде арккосинуса, а также в виде арктангенса.
Ниже приведены образцы соответствующих преобразований.
1. Преобразуем в арккосинус ![]() , где
, где ![]() и
и ![]()
Имеем:
![]()
Откуда
![]()
Похожие работы
... по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (4). Приняв во внимание равенство получим: Выполнение обратных тригонометрических операций над тригонометрическими функциями. При преобразовании выражений вида следует принимать во внимание в какой четверти находится аргумент х и в каком промежутке находится значение ...
... . Частные случаи тригонометрических уравнений Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями. Тригонометрические уравнения Аксиомы стереометрии и следствия из них Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых ...
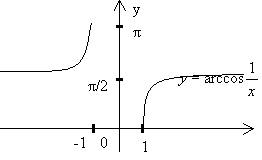
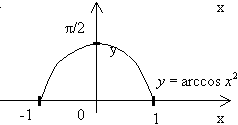
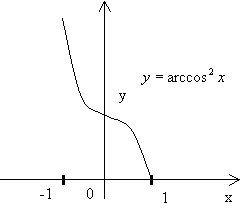
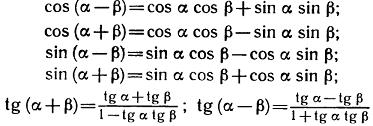
0 комментариев