Навигация
Выражение арксинуса через арккосинус
15614
знаков
10
таблиц
8
изображений
4. Выражение арксинуса через арккосинус.
Пусть 
, если 
, то 
. Дуга имеет косинус, равный 
, а поэтому 
При 
это равенство выполняться не может. В самом деле, в этом случае
, а для функции 
имеем: 
так как аргумент арккосинуса есть арифметический корень , т.е. число неотрицательное.
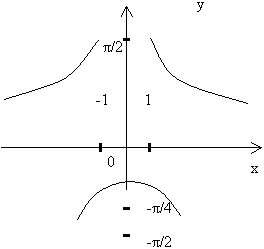
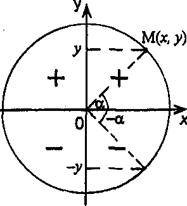
Расположение рассматриваемых дуг пояснено на рисунке:
 |  |
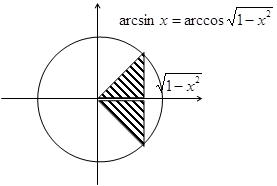Х>0 X<0
При отрицательных значениях Х имеем Х<0, а при положительных X>0, и
Таким образом, имеем окончательно:
если , (4)
, если 
График функции
 | ||||||
|
| |||||
Область определения есть сегмент [-1;1]; согласно равенству (4), закон соответствия можно выразить следующим образом:
 |
, если 
, если
5. Аналогично установим, что при имеем:
, если же , то
Таким образом:
, если (5)
, если
Похожие работы
... по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (4). Приняв во внимание равенство получим: Выполнение обратных тригонометрических операций над тригонометрическими функциями. При преобразовании выражений вида следует принимать во внимание в какой четверти находится аргумент х и в каком промежутке находится значение ...
... . Частные случаи тригонометрических уравнений Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями. Тригонометрические уравнения Аксиомы стереометрии и следствия из них Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых ...
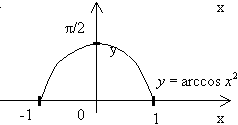
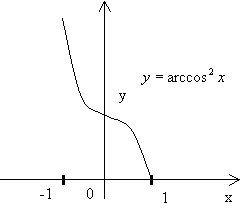
0 комментариев