Аналогично

2.    Аналогично

, где 0 < x < 1, 0 < y < 1

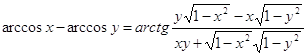, где 0 < x < 1, 0 < y < 1

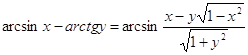
Формулы сложения аркфункций от произвольных аргументов.

1.    Выразить сумму через арксинус

По определению арксинуса

и ,

откуда

Для дуги γ возможны следующие три случая:

Случай 1:

Если числа x и y разных знаков или хотя бы одно из них равно нулю, то имеет место случай 1.

В самом деле, при и , имеем:

, и ,

откуда

При x > 0, y > 0 для дуги γ имеет место одна из следующих двух систем неравенств:

а) б)

Необходимым и достаточным признаком, позволяющим отличить один от другого случаи а) и б), является выполнение неравенства:

 в случае а) и  в случае б)

В самом деле, взаимно исключающие друг друга соотношения а) и б) влекут за собой взаимно исключающие следствия  и (соответственно), а потому эти следствия служат необходимыми и достаточными признаками наличия данных соотношений.

Вычислив , получим:

При x > 0, y > 0 наличие случая 1 означает выполнения неравенства а) т.е. или

Откуда

 и, следовательно,

Наличие случая 1 при x < 0, y < 0 означает выполнение неравенств

;

но тогда для положительных аргументов –x и –y имеет место случай 1, а потому

 или

Случай 2.

В этом случае x > 0, y > 0, т.е. выполняется неравенство б); из условия получим

Случай 3.

Этот случай имеет место при x < 0, y < 0, и

Изменив знаки на противоположные придем к предыдущему случаю:

откуда

Дуги γ и  имеют одинаковый синус, но (по определению арксинуса) , следовательно в случае 1 ;

в случае 2  и в случае 3 .

Итак, имеем окончательно:

 ,  или

; x > 0, y > 0, и  (1)

; x < 0, y < 0, и

Пример:

;

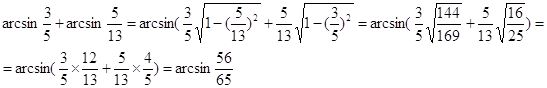
2. Заменив в (1) x на –x получим:

 ,  или

; x > 0, y > 0, и  (2)

; x < 0, y < 0, и

3. Выразить сумму через арккосинус

и

имеем

Возможны следующие два случая.

Случай 1: если , то

Приняв во внимание, что обе дуги и расположены в промежутке [0;π] и что в этом промежутке косинус убывает, получим

и следовательно, , откуда

Случай 2: . Если , то

,

откуда при помощи рассуждений, аналогичных предыдущим, получим . Из сопоставления результатов следует, что случай 1 имеет место, если , а случай 2, если

.

Из равенства  следует, что дуги

 и  имеют одинаковый косинус.

В случае 1 , в случае 2 , следовательно,

,

, (3)

4. Аналогично

,

, (4)

 

пример:

5.

; xy < 1

; x > 1, xy > 1 (5)

; x < 0, xy > 1

При xy=1 не имеет смысла

6.

; xy > -1

; x > 0, xy < -1 (6)

; x < 0, xy < -1

7.

;

; (7)

;

8.

; (8)

;

9.

;

; x > 1 (9)

; x < -1

10. (10)

(11)

 , если (12)

, если