Навигация
Асимптоты (определение, виды, правила нахождения)
МОСКОВСКИЙ ИНСТИТУТ ЭКОНОМИКИ,
МЕНЕДЖМЕНТА И ПРАВА
РЕФЕРАТ
по дисциплине: Высшая математика
на тему: Асимптоты (определение, виды, правила нахождения)
Выполнила: студентка 1 курса
Экономического факультета
(вечернее отделение)
Козлова М.А.
Проверил: Рошаль А.С.
Москва 2002 год
2
Содержание Введение 32. Нахождение асимптоты 4
2.1 Геометрический смысл асимптоты 5
2.2 Общий метод нахождения асимптоты 6
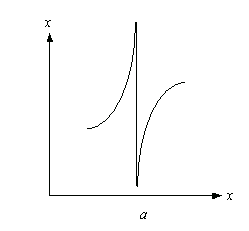
3. Виды 8
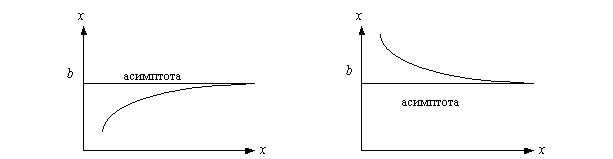
3.1 Горизонтальная асимптота 8
3.2 Вертикальная асимптота 9
3.3 Наклонная асимптота 10
Использованная литература 123
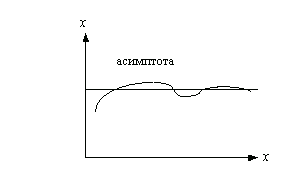
ВведениеАсимптота, так называемая прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, но никогда не пересекает ее, так что расстояние между ними делается бесконечно малой величиной.
Понятие асимптоты играет важную роль в математическом анализе. Они проводятся при изучении свойств многих кривых (гиперболы, конхоиды, логарифмич. линии, циссоиды и др.).
4
2. Нахождение асимптоты
Пусть функция f (x) определена для всех x > а (соответственно для всех
x < а). Если существуют такие числа k и l, что f(x) - kx - l = 0 при х ® + ¥ (соответственно при х ® - ¥), то прямая
y = kx + l
называется асимптотой графика функции f (x) при x ® + ¥ (соответственно при х ® - ¥).
Существование асимптоты графика функции означает, что при х ® + ¥
(или х ® - ¥) функция ведёт себя «почти как линейная функция», то есть отличается от линейной функции на бесконечно малую.
![]() x
x![]() - 3x - 2
- 3x - 2
Найдём, например, асимптоту графика функции y = x +1
Разделив числитель на знаменатель по правилу деления многочленов,
![]()
![]() 2 2
2 2
получим y = x - 4 + x + 1 Так как x + 1 = 0 при х ® ± ¥, то прямая y = x-4
является асимптотой графика данной функции как при х ® + ¥,
так и при х ® - ¥.
5
2.1 Геометрический смысл асимптоты
Рассмотрим геометрический смысл асимптоты. Пусть М = (x, f (x)) – точка графика функции f, М![]() - проекция этой точки на ось Ох, АВ – асимптота,
- проекция этой точки на ось Ох, АВ – асимптота,
q - угол между асимптотой и положительным направлением оси Ох, q ¹![]() ,
,
MP – перпендикуляр, опущенный из точки М на асимптоту АВ, Q – точка пересечения прямой ММ![]() с асимптотой АВ (рис.1).
с асимптотой АВ (рис.1).
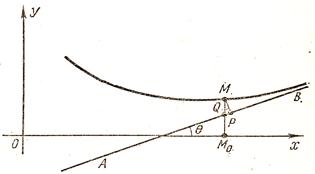
(рис.1)
Тогда ММ![]() = f (x), QM
= f (x), QM![]() = kx + l, MQ = MM
= kx + l, MQ = MM![]() - QM
- QM![]() = f (x) – (kx +l),
= f (x) – (kx +l),
MP = MQ cos q. Таким образом, MP отличается от MQ лишь на не равный нулю множитель cos q, поэтому условия MQ ® 0 и MP ® 0 при х ® + ¥ (соответственно при х ® - ¥) эквивалентны, то есть lim MQ = 0,
то и lim MP = 0, и наоборот. х ® + ¥
х ® + ¥
Отсюда следует, что асимптота может быть определена как прямая, расстояние до которой от графика функции, то есть отрезок МР, стремится к нулю, когда точка М = (x, f (x)) «стремится, оставаясь на графике, в бесконечность» (при х ® + ¥ или, соответственно, х ® - ¥).
6
Похожие работы
... утверждение: если существуют такие числа k и l, что выполняется условие l = lim (f (x) – kx), то прямая y = kx + l является х ® + ¥ асимптотой графика функции f (x). В самом деле, из l = lim (f (x) – kx) имеем х ® + ¥ lim [f (x) - (kx + l)] = 0, х ® + ¥ то есть прямая y ...
... устройства, которое нужно добавить к некоторой неизменяемой части системы, чтобы обеспечит требуемое качество системы в установившемся и переходном режимах. Наиболее приемлемым для решения задачи динамического синтеза является метод логарифмических амплитудных характеристик (метод ЛАХ). [1, § 12.5] Стадии синтеза по методу ЛАХ включают: 1. построение располагаемой ЛАХ, т.е. ЛАХ исходной ...
... данным, n=20 Найти матрицу А-1, обратную к матрице А и с ее помощью решить систему А =, где , = , = . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИКА (углубленный курс) Билет № 12 Что называется характеристическим уравнением дифференциального уравнения II порядка с постоянными коэффициентами? По какой ...
ывают определением на «языке последовательностей». Второе определение носит название «на языке ». Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции при , если для любого числа существует такое число d, что при всех справедливо неравенство : . Теоремы о пределах функций являются базой для ...
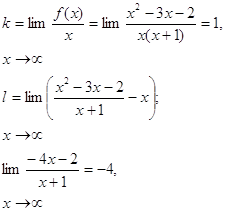


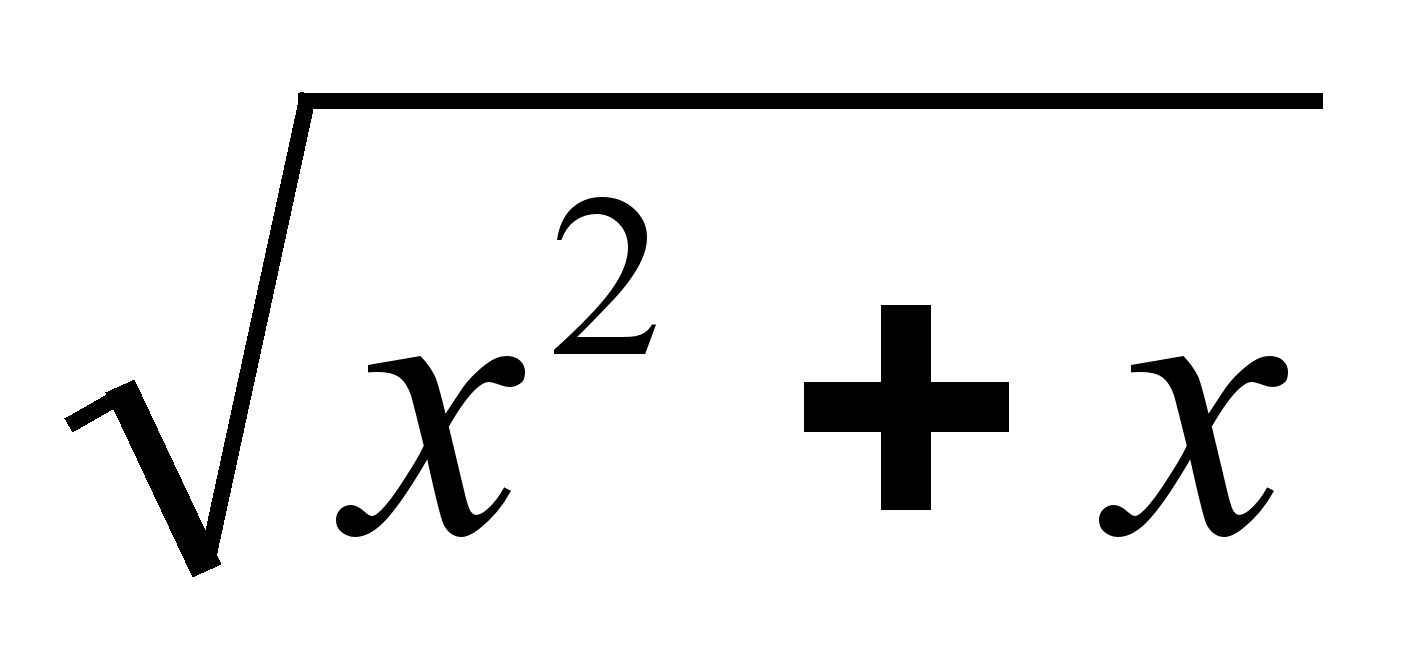


0 комментариев