Высшая математика

Контрольная работа

высшая математика

ЗАДАЧА 1. Вычислить пределы функций а) —д):

а) 1..

►==.

2. .

►.====0.

3. ..

►.====-∞.

б) .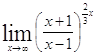

Решение.==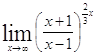

==

 ===

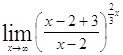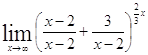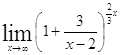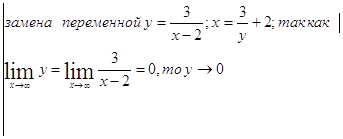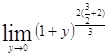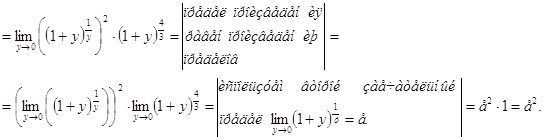
Предел  вычислен подстановкой

Предел  не может быть вычислен подстановкой , поскольку в результате подстановки получается неопределенность .

в) .

Анализ задачи. Подстановка числа 2 вместо  показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность . Для этого можно либо провести тождественные преобразования выражения , либо применить правило Лопиталя.

Решение. Выражение  является сопряженным по отношению к выражению , а выражение  - по отношению к . Умножая числитель и знаменатель дроби на произведение сопряженных выражений ()·(), и используя формулу разности квадратов , получаем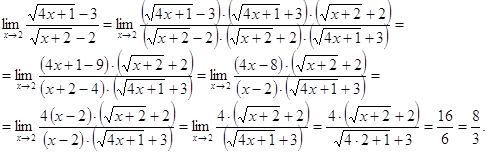

Другое решение задачи. Воспользуемся правилом Лопиталя

Ответ:

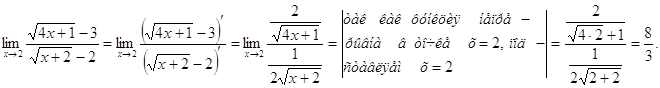
Анализ задачи. В данном случае, непосредственное применение те­оремы о пределе частного невозможного, поскольку, как показывает подстановка числа. -3 вместо x и предел числителя и предел знаме­натели равны пулю.

 и

Таким образом, рассматриваемый предел представляет собой неопределённость вида  и для решения задачи требуется про­вести тождественные преобразования выражения, находящего­ся под знаком предела.

Решение. Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если— корни квадратного трехчлена, то,

= Решаем квадратное уравнение, находя его дискриминант D.

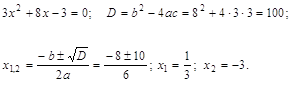
Отсюда,

Аналогично,

Поэтому,

Преобразуем выражение находящиеся под знаком предела:

 ==

=

Другое решение задачи. Поскольку пределы числителя и знаменателя при

Равны нулю, применимо правило Лопиталя.

	Ответ:10.

д)

Анализ задачи. Подстановка числа 0 вместо x показывает, что пределы числителя и знаменателя при  равны нулю. Поэтому, имеет место неопределённость .

Для того, чтобы раскрыть неопределённость можно либо провести тождественные преобразования выражения, либо применить правило Лопиталя.

Решение. Совершим замену неизвестной при этом

Так как  при то

Используем теперь тригонометрическую формулу

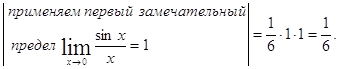
Другое решение. Воспользуемся вновь правилом Лопиталя

	Ответ:

ЗАДАЧА 2. Вычислить производные функций а) – в):

а) Вычислить производную функции

►◄

б) Вычислить производную функции

1. .

►

◄

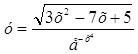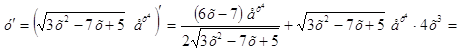
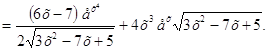в) Вычислить производную функции

.

►.◄

2. .

►

.◄

3.

►

.◄

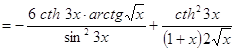ЗАДАЧА 3. Исследовать функцию и построить график

Исследовать функцию  и построить её график.

►Исследуем данную функцию.

1.           Областью определения функции является множество .

2.           Ордината точки графика .

3.           Точки пересечения графика данной функции с осями координат:

4.           Легко находим, что

.

Находим наклонные асимптоты:

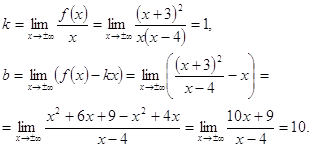
Таким образом, существует единственная наклонная асимптота