ПОБУДОВА ЕКОНОМІКО-МАТЕМАТИЧНОЇ МОДЕЛІ ОПТИМІЗАЦІЇ

2 ПОБУДОВА ЕКОНОМІКО-МАТЕМАТИЧНОЇ МОДЕЛІ ОПТИМІЗАЦІЇ

2.1 Аналітичний огляд літературних джерел

Широке застосування математичних методів є важливим напрямом удосконалювання економічного аналізу, підвищує ефективність аналізу підприємств і їхніх підрозділів. Це досягається за рахунок скорочення термінів проведення аналізу, більш повного охоплення впливу факторів на результати комерційної діяльності, заміни наближених і спрощених розрахунків точними обчисленнями, постановки і рішення нових багатомірних задач аналізу, практично нездійсненних вручну і традиційними методами.

Застосування математичних методів в економічному аналізі вимагає:

·     системного підходу до вивчення економіки підприємств, обліку всієї безлічі істотних взаємозв'язків між різними сторонами діяльності підприємств;

·     розробки комплексу економіко-математичних моделей, що відображають кількісну характеристику економічних процесів і задач, розв'язуваних за допомогою економічного аналізу;

·     удосконалювання системи економічної інформації про роботу підприємств;

·     наявності технічних засобів (ЕОМ і ін.), що здійснюють збереження, обробку і передачу економічної інформації з метою економічного аналізу;

·     організації спеціального колективу аналітиків, що складається з економістів-виробничників, фахівців з економіко-математичного моделювання, математиків-обчислювачів і ін^[4].

Застосування у фінансово-економічному аналізі математичних методів моделювання господарських процесів для розв’язання аналітичних задач – це шлях підвищення ефективності аналітичної роботи[14].

Застосування математики в економіці приймає форму економіко-математичного моделювання. За допомогою економіко-математичної моделі зображуються той чи інший дійсний економічний процес. Така модель може бути сконструйована тільки на основі глибокого теоретичного дослідження економічної сутності процесу. Тільки в цьому випадку математична модель буде адекватна дійсному економічному процесові, буде об'єктивно відображати його[4].

Математичне програмування – швидко розвиваючийся розділ сучасної прикладної математики. Методи математичного програмування – основний засіб вирішення задач оптимізації виробничо-господарської діяльності. По своїй суті – це методи планових розрахунків. Цінність їх для економічного аналізу виконання бізнес-планів полягає в тому, що вони дозволяють оцінювати напруженість планових завдань, визначати лімітовані групи устаткування, види сировини і матеріалів, одержувати оцінки дефіцитності виробничих ресурсів та інше.

Під дослідженням операцій розуміється розробка методів цілеспрямованих дій (операцій), кількісна оцінка отриманих рішень і вибір з них найкращого. Предметом дослідження операцій є економічні системи, у тому числі виробничо-господарська діяльність підприємств. Метою є таке сполучення структурних взаємозалежних елементів систем, що найбільшою мірою відповідає задачі одержання найкращого економічного показника з ряду можливих^[4].

Зв'язок аналізу і математики обумовлюється тим, що і тієї й іншої галузі знань властиве вивчення кількісних відносин. Застосування математики в економічних дослідженнях і розрахунках поширюється в першу чергу на галузь змінних величин, зв'язаних між собою функціональною залежністю. Сама змінна величина з'явилася у свій час поворотним пунктом у математиці. Завдяки цьому в математику увійшли рух і тим самим діалектика, і завдяки цьому стало необхідно диференціальне й інтегральне вирахування.

Вивчення змінних величин, вимір залежності одних перемінних від інших зводяться до визначення значення функції. Зв'язок між змінними величинами математично виражається у виді функціональних рівнянь, до яких, власне кажучи, відносяться диференціальні й інтегральні рівняння.

В економіці суцільно і поруч доводиться мати справу зі змінними величинами. Економічні перемінні, що мають якісну і кількісну визначеність, можуть бути у функціональній залежності друг від друга. Вивчення кількісних співвідношень і функціональних залежностей економічних перемінних являється однією з задач математики.

Багато економічних і математичних задач зводяться до перебування максимуму (мінімуму) функції декількох перемінних. Основною метою рішення задачі керування деякими галузями промисловості, сільського господарства, транспорту звичайно є досягнення деякого оптимального режиму роботи. У цих випадках задачі максимізації (мінімізації) звичайно називають задачами оптимізації, а максимізуючу (мінімізуючу) функцію – цільовою функцією.

Нехай функція W(x) = W(x₁, x₂, …, x_i) i перемінних визначена і безупинна в області. Точка х* = {х₁*, х₂*,..., х_i*) D називається точкою локального максимуму (мінімуму) функції W(х), якщо існує деяка ε— околиця точки x*, така, що для всіх х = (x₁, x₂, …, x_i) з цієї околиці виконуються нерівності

W(x)≥ W(x*) (W(x)≤ W(x*)), (2.1.1)

де i = 1, 2,…,n

Необхідні умови екстремуму діфференцируємої функції W(x), як відомо, можна представити у виді системи і нелінійних рівнянь

 (2.1.2)

Точки, що визначають рішення системи (2.1.2), називаються стаціонарними. Якщо в околиці ρ(х⁰) стаціонарної точки х⁰ = (х₁, х₂, …, х_n) функція W(x) є опуклої, тобто для будь-якого 0 ≤ α ≤ 1

 (2.1.3)

де стаціонарна точка х⁰ є точкою максимуму (мінімуму). Зокрема, якщо в околиці стаціонарної точки х⁰ функція W(x) двічі безупинно дифференцируема і її матриця Гессе позитивно визначена в х⁰, то функція W(x) буде опуклої, а х⁰— точкою мінімуму.

Щоб симетрична матриця А — [a_ij ] (a_ij = a_ji)була позитивно визначеною, необхідно і досить, щоб кожний з її головних мінорів був позитивний (критерій Сильвестра).

Рішення системи нелінійних рівнянь (2.1.2) і перевірка позитивної визначеності матриці Гессе вимагають великого обсягу обчислень. При цьому часто зустрічаються недифференцируемые функції, або функції, похідні яких записуються громіздкими аналітичними вираженнями. Тому більш ефективними є чисельні методи рішення задачі, що не вимагають перевірки умов (2.1.3).

Чисельне рішення задач максимізації (мінімізації) зводиться до побудови ітерацій  таких, що послідовність { x₁, x₂, …, x_i } є максимізуючою (мінімізуючою), тобто

.

У залежності від характеру побудови dⁿ чисельні методи розділяються на прямі (без використання похідних), методи спуска (з використанням перших похідних) і методи з використанням других похідних.

Існує безліч методів рішення поставленої задачі. Розглянемо деякі з тих, за допомогою яких можна вирішити запропоновану модель.

Класичні методи визначення екстремумів

У багатьох економічних моделях дослідження операцій залежності між постійними і перемінними факторами лише в першому наближенні можна вважати лінійними, більш детальний розгляд дозволяє знайти їхня нелінійність. Як правило, такі показники, як прибуток, собівартість, капітальні витрати на виробництво й ін., у дійсності залежать від обсягу виробництва, витрати ресурсів і т.п., нелінійно. У цьому випадку виникає задача нелінійного програмування.

Можна виділити клас нелінійних задач, що відносяться до класичних методів оптимізації. Припустимо, що серед обмежень математичної моделі немає нерівностей, не обов'язкові умови незаперечності, перемінні не є дискретними, m < n, а цільові функції безперервні і мають частки похідні принаймні другого порядку. У цьому випадку задачу оптимізації можна сформулювати так: знайти перемінні х_1, х₂,..., х_M, що задовольняють системі рівнянь

 (2.1.4)

і обертаючі в максимум (мінімум) цільову функцію

(2.1.5)

Такі задачі в принципі можна вирішувати класичними методами диференціального вирахування. Однак на цьому шляху зустрічаються такі обчислювальні труднощі, що роблять необхідним пошук інших методів рішення. Тому класичні методи часто використовуються не як обчислювальний засіб, а як основа для теоретичного аналізу.

Прикладом типової і простої нелінійної задачі є наступна: дане підприємство для виробництва якогось продукту витрачає два засоби в кількості х₁ і х₂ відповідно. Це фактори виробництва, наприклад, машини і праця, два різних види сировини і т.п., а величини х₁ і х₂ — витрати факторів виробництва. Фактори виробництва надалі будемо вважати взаємозамінними. Якщо це "праця" і "машини", то можна застосовувати такі методи виробництва, при яких величина витрат машин у зіставленні з величиною витрат праці виявляється більше або менше (виробництво більш-менш трудомістке). У сільському господарстві взаємозамінними факторами можуть бути посівні площі або мінеральні добрива (екстенсивний або інтенсивний метод виробництва).

Обсяг виробництва (виражений у натуральних або вартісних одиницях) є функцією витрат виробництва  Ця залежність називається виробничою функцією. Витрати залежать від витрати обох факторів (х₁ і х₂) і від цін цих факторів (з₁ і з₂). Сукупні витрати виражаються формулою b=c₁x₁+c₂x₂. Потрібно при даних сукупних витратах визначити таку кількість факторів виробництва, що максимізує обсяг продукції z.

Математична модель цієї задачі має вигляд:

Визначити такі перемінні х₁ і х₂, що задовольняють наступним умовам

c₁x₁+c₂x₂= b, (2.1.6)

x₁ ≥ 0, x₂ ≥ 0 (2.1.7)

при яких функція  досягає максимуму.

Як правило, функція (2.1.7) може мати довільний нелінійний вид.

Використовуючи класичні методи оптимізації, варто чітко уявляти собі розходження між локальним екстремумом функції, глобальним екстремумом і умовним екстремумом. При цьому корисно повторити визначення локального і глобального екстремумів для функції однієї перемінної. Поняття умовного екстремуму вводиться для випадку, коли число перемінних n не менше 2 (n≥2).

Будемо думати, що функція  двічі діфференцується в точці , і в деякій її околиці. Якщо для всіх точок X цієї околиці , то говорять, що функція f(X) має екстремум у X^* (відповідно максимум або мінімум).

Точка Х^*, у якій усі частки похідні функції z = f (X) рівні 0, називається стаціонарною точкою.

Необхідна умова екстремуму. Якщо в точці Х^* функція z = f (X) має екстремум, то частки похідні функції в цій точці рані нулеві:

Отже, точки екстремуму функції z = f (X) задовольняють системі рівнянь (1.5.5):

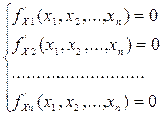(2.1.8)

Як і у випадку одна перемінної, необхідне умова не є достатнім для того, щоб стаціонарна точка була точкою екстремуму. Для одержання достатніх умов варто визначити в стаціонарній точці знак диференціала другого порядку. Диференціал другого порядку позначається d² f (x₁, x₂,…,x_n)і дорівнює сумі добутків часток похідних другого порядку на відповідні збільшення аргументів. Якщо від частинної похідної знайти частинну похідну по перемінній х_j, то одержимо частинну похідну другого порядку по перемінним х_i, х_j, що позначається . У цьому випадку

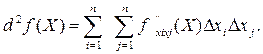
Достатні умови екстремуму:

а) у стаціонарній точці X⁰ функція  має максимум, якщо < 0, і мінімум, якщо > 0, при будь-яких ; (у цих випадках Х⁰ = Х^*), що не звертаються в нуль одночасно;

6) якщо  може приймати в залежності від і позитивні, і негативні значення, то в точці X⁰ екстремуму немає;

в) якщо може звертатися в нуль не тільки при нульових збільшеннях , то питання про екстремум залишається відкритим.

Для функції двох перемінних достатні умови ще не дуже складні. Існують чотири частки похідні другого порядку: . З них дві змішані похідні , якщо безперервні, те рівні.

Знайдемо значення часток похідних другого порядку в стаціонарній точці Х⁰(х⁰₁,х⁰₂):

(можна переконатися, що а₁₂ = а₂₁). Позначимо через ∆ визначник, складений з а_ij для i, j = 1,2:

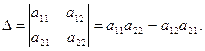
Тоді достатні умови екстремуму функції двох перемінних мають вигляд:

а) якщо ∆ > 0 і а₁₁ < 0 (а₂₂ < 0), те в точці Х⁰ функція має максимум: якщо ∆ > 0 і а₁₁ > 0 (а₂₂ > 0), те в точці Х⁰ — мінімум (у цих випадках Х⁰ = Х ^');

б) якщо ? < 0, те екстремуму немає;

в) якщо ∆ = 0, то питання про екстремум залишається відкритим.

Схема визначення екстремуму функції n перемінних збігається з правилами визначення локального екстремуму функції однієї перемінної.

Умовний екстремум.

Нехай необхідно знайти екстремум функції за умови, що перемінні  задовольняють рівнянням (2.1.9)

 (2.1.9)

Передбачається, що функції f і φ_i, мають безперервні частки похідні по всім перемінним. Рівняння (2.1.9) називають рівняннями зв'язку.

Говорять, що в точці Х⁰ = , що задовольняє рівнянням зв'язку (1.5.6), функція  має умовний максимум (мінімум), якщо нерівність  має місце для всіх точок X, координати яких задовольняють рівнянням зв'язку.

Легко помітити, що задача визначення умовного екстремуму збігається з задачею нелінійного програмування (2.1.4), (2.1.5).

Один зі способів визначення умовного екстремуму застосовується в тому випадку, якщо з рівнянь зв'язку (2.1.9) n перемінних, наприклад  можна явно виразити через що залишилися n-m перемінних:

 (2.1.10)

Підставивши отримані вираження для , у функцію z, одержимо

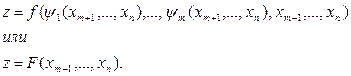 (2.1.11)

Задача зведена до перебування локального (глобального) екстремуму для функції (2.1.11) від n-m перемінних. Якщо в точці Х⁰ =  функція (2.1.11) має екстремум, то в точці  функція має умовний екстремум.

Метод множників Лагранжа

Інший спосіб визначення умовного екстремуму починається з побудови допоміжної функції Лагранжа, що в області припустимих рішень досягає максимуму для тих же значень перемінних х₁, х₂,..., х_n, що і цільова функція z.

Нехай вирішується задача визначення умовного екстремуму функції  при обмеженнях (2.1.9).

Складемо функцію, що називається функцією Лагранжа.

, (2.1.12)

де  постійні множники (множники Лагранжа). Відзначимо, що множникам Лагранжа можна додати економічний зміст. Якщо  — доход, що відповідає планові , а функція  — витрати і-го ресурсу, що відповідають цьому планові, то — ціна (оцінка) і-го ресурсу, що характеризує зміну екстремального значення цільової функції в залежності від зміни розміру і-го ресурсу (маргінальна оцінка). L(X) — функція m+n перемінних . Визначення стаціонарних точок цієї функції приводить до рішення системи рівнянь

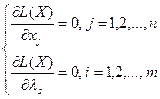 (2.1.13)

Легко помітити, що , тобто в (5.10) входять рівняння зв'язку. Таким чином, задача перебування умовного екстремуму функції  зводиться до перебування локального екстремуму функції L(X). Якщо стаціонарна точка знайдена, то питання про існування екстремуму в найпростіших випадках вирішується на підставі достатніх умов екстремуму — дослідження знака другого диференціала d²L(X) у стаціонарній точці за умови, що перемінні збільшення ∆_xj зв'язані співвідношеннями, отриманими шляхом диференціювання рівнянь зв'язку.

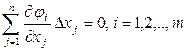(2.1.14)

Задача опуклого програмування (ОП)

Нехай дана система нерівностей виду

  (2.1.15)

 і функція

(2.1.16)

причому усі функції  є опуклими на деякій опуклій безлічі М, а функція Z або опукла на безлічі М, або увігнута. Задача опуклого програмування (ОП) складається у відшуканні такого рішення системи обмежень (2.1.15), при якому цільова функція Z досягає мінімального значення, або увігнута функція Z досягає максимального значення. (Умови незаперечності перемінних можна вважати включеними в систему (2.1.15)).

Усяка задача лінійного програмування є часткою случаємо задачі опуклого програмування (ОП). У загальному випадку задачі ОП є задачами нелінійного програмування. Виділення задач ОП у спеціальний клас порозумівається екстремальними властивостями опуклих функцій: усякий локальний мінімум опуклої функції (локальний максимум увігнутої функції) є одночасно і глобальним; крім того, задана на замкнутій обмеженій безлічі, досягає на цій безлічі глобального максимуму і глобального мінімуму. Звідси випливає, що якщо цільова функція Z є строго опуклою (строго увігнутої) і якщо область рішень системи обмежень не порожня й обмежена, то задача ОП завжди має єдине рішення. У цьому випадку мінімум опуклої (максимум увігнутої) функції досягається усередині області рішень, якщо там мається стаціонарна точка, або на границі цієї області, якщо усередині неї немає стаціонарної точки. (У загальному випадку можна затверджувати лише, що безліч оптимальних рішень будь-якої задачі ОП є опуклою безліччю).

Наближене рішення задач опуклого програмування методом кусочно-лінійної апроксимації

Функція  називається сепарабельной, якщо її можна представити у виді суми функцій, кожна з яких залежить тільки від однієї перемінної, тобто якщо

 (2.1.17)

(не виключено, що F_i(x_i) = 0 при деяких i).

Нехай у задачі ОП (2.1.15), (2.1.16) і функція мети Z, і всі обмеження , є сепарабельними. Тоді задача має вигляд: знайти мінімум опуклої (максимум увігнутої) функції , при обмеженнях

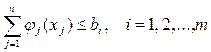 (2.1.18).

Ідея методу кусочно-лінійної апроксимації полягає в тому, що всі f_i, і всі , заміняються ламаними лініями, що складаються з прямолінійних відрізків. При цьому вихідна задача ОП заміняється новою, наближеною задачею, що є задачею лінійного програмування. Ця задача вирішується звичайно симплексним методом, і її рішення є наближеним рішенням вихідної задачі ОП.

Для побудови наближеної задачі розглянемо кусочно-лінійну апроксимацію функції одному перемінної h(х), заданої на відрізку [0, а]. Розіб'ємо цей відрізок на r частин точками х₀ < х₁ <...< х_r так, щоб х₀ = 0, х_r = а (малюнок 2.1.1).

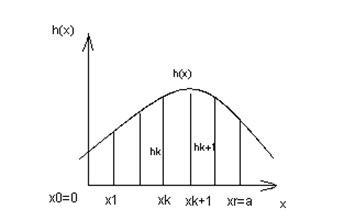
Рисунок 2.1.1 – Кусочно-лінійна апроксимація функції однієї перемінної

Обчислимо значення функції h_k(x), у цих точках. З'єднаємо попарно точки (х_k; h_k) і (х_k+1; h_k+1) відрізками прямих. Складена з цих відрізків ламана h(х) апроксимує функцію h(х) на відрізку [0, а]. (Не розглядаючи тут оцінку точності наближення, відзначимо тільки, що точність можна збільшити за рахунок більш дрібної розбивки відрізка).

Рівняння ділянки ламаної (х) між точками (х_k; h_k) і (х_k+1; h_k+1) має вигляд

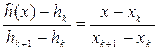
(рівняння прямої по двох точках). Якщо кожне з відносин у цій рівності позначити через, то одержимо (2.1.19):

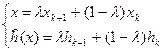  (2.1.19)

причому

Відзначимо, що для кожного існує єдине значення , що задовольняє умовам (2.1.19). Позначивши , можна представити у виді:

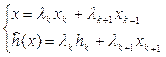(2.1.20)

де

(Рівняння (2.1.20) називаються параметричними рівняннями відрізка. Якщо h(x)=0, те друге з цих рівнянь звертається в тотожність 0 = 0.

Таким чином, для будь-якого рівняння ламаної можна записати у виді:

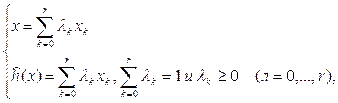 (2.1.21)

причому завжди відмінні від нуля тільки два значення  (якщо х є внутрішньою точкою k-го відрізка розбивки) або одне (якщо х збігається з кінцем відрізка).

Повертаючи до задачі ОП із сепарабельними функціями, відзначимо, що насамперед (у залежності від системи обмежень) потрібно визначити інтервал зміни кожної перемінної х_j. Потім кожен цей інтервал розбивається на частині точками х_jk і з використанням формул (2.1.21) будується кусочно-лінійна апроксимація для функцій f_j і. Після цього можна для вихідної задачі (2.1.18) записати наближену задачу:

знайти максимум функції

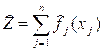
при обмеженнях

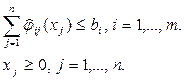 (2.1.22)

Оскільки наближена задача (2.1.22) є задачею лінійного програмування і ми звичайно вирішуємо її симплексним методом, умови незаперечності перемінних записуються окремо від інших обмежень. Відмінність отриманої задачі (2.1.22) від звичайної задачі лінійного програмування полягає в тому, що для кожного x_j мається не більш двох сусідніх ненульових  з однаковим j і несусідніми k. Помітимо також, що для умов незаперечності перемінних що складаються f_j(x_j) і  (якщо такі виявляться) кусочно-лінійну апроксимацію проводити, звичайно, не потрібно.[9]