Навигация
Вибір методу оптимізації закупівель
2.4 Вибір методу оптимізації закупівель
Сформульована математична задача може бути вирішена одним з розроблених математичних методів. Методи елементарної математики використовуються в звичайних традиційних економічних розрахунках при обґрунтуванні потреб у ресурсах, обліку витрат на виробництво, розробці планів, проектів, при балансових розрахунках і т.д. Ці методи використовуються не тільки в рамках інших методів, але й окремо.
Існує безліч методів рішення поставленої задачі. Розглянемо деякі з тих, за допомогою яких можна вирішити запропоновану модель.
Метод покоординатного спуску
Цей метод є найбільш простим із прямих методів пошуку мінімуму функції декількох перемінних. Викладемо ідею методу для випадку функції двох перемінних f (x, y).
Виберемо початкове наближення M0 (х0, у0). Зафіксуємо в0 і знайдемо мінімум функції однієї перемінної f (x, y0). Нехай він досягається при х = х1. Уздовж прямій, рівнобіжній осі ОХ, здійснюємо спуск у точку Mt (х1, у0). Фіксуємо х1 і знаходимо мінімум функції однієї перемінної f (х1, у). Нехай це буде в1. З точки М1 (х1, у0) рухаємося уздовж прямій, рівнобіжній осі OY, до точки М2 (.x1, у1). Потім знову здійснюємо спуск із точки М2 уздовж прямої рівнобіжної осі ОХ і т.д. (рисунок 2.4.1).
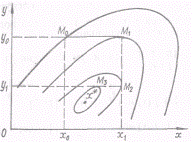
Рисунок 2.4.1 – Метод покоординатного спуска
Відомо, що якщо функція f (х, у) має безупинні другі похідні в околиці мінімуму, то при відповідному виборі початкового наближення (х0, у0) спуск по координатах сходиться до мінімуму. Зокрема, метод сходиться, якщо в області D, обмеженою лінією рівня, що проходить через точку М0 {х0, у0), виконуються умови:
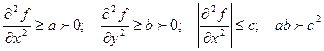 (2.4.1)
(2.4.1)
Частки похідні функції прагнуть до нуля. Метод сходиться зі швидкістю геометричної прогресії.
Метод градієнтного спуску
Метод визначення мінімуму функції f(х), х=(x1, x2,..., хп), називаний методом градієнтного чи найшвидшого спуска, запропонованийі Коши.
Для мінімізації по методу спуска вибирається початкова точка х0= (х01, х02,..., х0n) (звичайно відповідно до фізичного змісту задачі). Функція f (x) = f (х0) визначає в n-мірному просторі гіперповерхня, градієнт якого вказує напрямок найшвидшого зростання функції.
Тому в напрямку — grad f(х0) функція швидше за все убуває при нескінченно малому русі з даної точки. Спуск по цьому напрямку до мінімуму визначає нове наближення х1.. У цій точці знову визначається градієнт і здійснюється спуск у напрямку антиградієнта. Випадок п = 2 представлений на рисунку 2.4.2
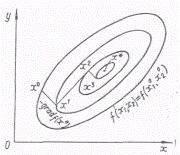
Малюнок 2.4.2 – Метод градієнтного спуску для n=2
Вектор х, який було необхідно знайти послідовно уточнюється на k-й ітерації методу градієнтного спуска по формулі 2.4.2.
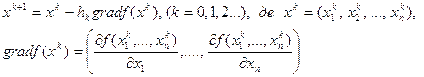 ,
,
де hk — оптимальний крок для k -й ітерації.
Таким чином, на кожнім кроці градієнтного спуска потрібно вирішувати ще задачу мінімізації функції одним перемінної яким-небудь чисельним методом. Зокрема, можна розкласти функцію в ряд Тейлора, обмеживши членами другого порядку, і визначити hk. Однак такий метод приводить до дуже громіздких обчислень. При цьому необхідно враховувати також трудомісткість обчислення значень функції f(х) і її градієнта в точках хк. Тому на практиці часто h вибирають емпіричним шляхом. Здійснюється спуск при довільному hk; якщо значення функції f (хk+1) зменшиться, те переходимо до наступного кроку спуска, якщо ж f (хk+1) не убуває, те зменшуємо крок hk. Варто враховувати, що якщо hk вибрати дуже малим, те це приводить до істотного збільшення обсягу обчислень, якщо hk занадто велике, те це може привести до проскакування через мінімум функції. Обчислення по формулі (2.4.2) проводимо доти, поки функція f(х) практично перестане убувати, тобто до виконання для наперед заданого ε нерівності ![]()
Критерієм закінчення ітераційного процесу пошуку мінімуму можна вибрати також умова:
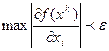
Метод Ньютона
Описаним вище методам властивий один загальний недолік — повільна збіжність, якщо поверхні (лінії) рівня мінімізуємої функції витягнуті, сильно відрізняються від сфер (окружностей). У методі Ньютона мінімізації функції декількох перемінних цей недолік усувається обліком значень других похідних, однак застосуємо цей метод для більш вузького класу функцій.
Нехай в околиці стаціонарної точки х* функція f (x)= f (х1,..., хп) двічі безупинно дифференцируема і її матриця Гессе

позитивно визначена. Тоді, застосовуючи для рішення системи
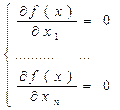
(2.4.3)
метод Ньютона, або модифікований метод Ньютона, одержимо ітераційний процес для мінімізації функції або
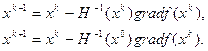 (2.4.4)
(2.4.4)
Позитивна визначеність матриці Н (х) забезпечує збіжність методу Ньютона до рішення системи (2.2.3), причому збіжність буде квадратичної, а при застосуванні модифікованого методу Ньютона — лінійної.
Приведемо на рисунку 2.2.3 блок-схему рішення вищевикладеного методу
Ітераційний процес (2.4.4) називають методом Ньютона (модифікованим методом Ньютона) мінімізації функції f(х) п перемінних х = (x1, x2,..., хп).
Варто врахувати, що в методі Ньютона на погрішність накладається погрішність звертання матриці H(xk). У зв'язку з цим для функції п перемінних при великому п застосовують модифікований метод Ньютона (2.4.4). Відзначимо, що для квадратичної форми метод Ньютона дає точний результат при першій ітерації.
![]()
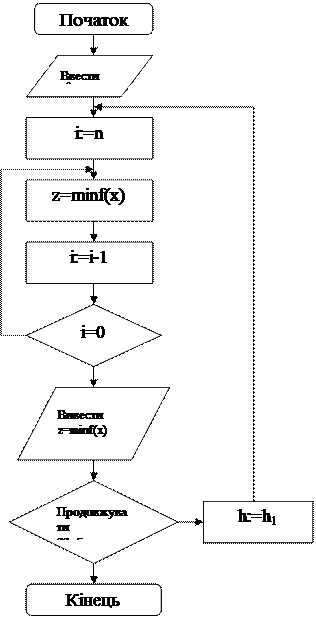
Рисунок 2.4.3 – Блок-схема рішення методу Ньютона
Збіжність має місце тоді, коли 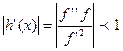 навколо xN. Якщо xN є простим коренем, то виконуються співвідношення f’(xN) ≠ 0 та h’(xN) = 0. Тобто, для початкового значення х(0) повинна виконуватися нерівність
навколо xN. Якщо xN є простим коренем, то виконуються співвідношення f’(xN) ≠ 0 та h’(xN) = 0. Тобто, для початкового значення х(0) повинна виконуватися нерівність
![]()
Ітераційна формула має вигляд:
![]()
Вибір методу рішення залежить від багатьох критеріїв: збіжність, одержання точних результатів і т.п. У нашому випадку головним критерієм є збіжність.
Для методів градієнтного і покоординатного спуска характерна повільна збіжність. Метод Ньютона за критерієм збіжності є самим оптимальної. Виходить, запропоновану математичну модель вирішимо методом Ньютона.
Математична модель включає математичні формули розрахунку основних показників, що формуються в процесі рішення задачі, а також, при необхідності, опис процесу (об'єкта), список можливих допущень і оцінку відповідності розробленої моделі реальному процесу (об'єкта).
Під час автоматизованого рішення задачі "Інформаційна система для обліку відвантаження і реалізації продукції" визначаються економічні показники, задані формулою (2.4.5).
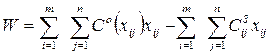 , де (2.4.5.)
, де (2.4.5.)
![]() – відпускна ціна i-го заводу j-й продукції;
– відпускна ціна i-го заводу j-й продукції; ![]() - закупівельна ціна i-го заводу j-й продукції,
- закупівельна ціна i-го заводу j-й продукції, ![]() - шуканий обсяг закупівель на i-м заводі j-й продукції.
- шуканий обсяг закупівель на i-м заводі j-й продукції.
0 комментариев