Навигация
Достаточные условия для точки локального минимума (максимума)
2. Достаточные условия для точки локального минимума (максимума)
Представим разложение функции ![]() в окрестности точки
в окрестности точки ![]() в ряд Тейлора с точностью до квадратичных по
в ряд Тейлора с точностью до квадратичных по ![]() слагаемых.
слагаемых.
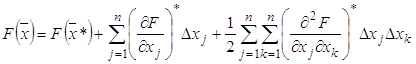 (1)
(1)
Разложение (1) можно представить более кратко, используя понятие: "скалярное произведение векторов" и "векторно-матричное произведение".
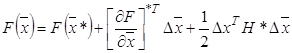 (1')
(1')
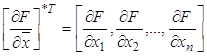
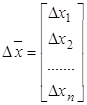
![]()
![]() - матрица двух производных от целевой функции по соответствующим переменным.
- матрица двух производных от целевой функции по соответствующим переменным.
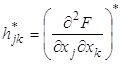 ,
, ![]()
Приращение функции ![]() на основании (1') можно записать в виде:
на основании (1') можно записать в виде:
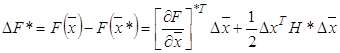 (3)
(3)
Учитывая необходимые условия:
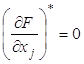 ,
, ![]() (4)
(4)
Подставим (3) в виде:
![]() (4')
(4')
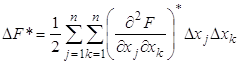 (5)
(5)
Квадратичная форма ![]() называется дифференциальной квадратичной формой (ДКФ).
называется дифференциальной квадратичной формой (ДКФ).
Если ДКФ положительно определена, то ![]() и стационарная точка
и стационарная точка ![]() является точкой локального минимума.
является точкой локального минимума.
Если же ДКФ и матрица ![]() , ее представляющая, отрицательно определены, то
, ее представляющая, отрицательно определены, то ![]() и стационарная точка
и стационарная точка ![]() является точкой локального максимума.
является точкой локального максимума.
Итак, необходимое и достаточное условие для точки локального минимума имеют вид
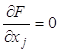
![]() (эти же необходимые условия можно записать так:
(эти же необходимые условия можно записать так:
![]() ,
, ![]() ,
, ![]() )
)
![]() - достаточное условие.
- достаточное условие.
Соответственно, необходимое и достаточное условие локального максимума имеет вид:
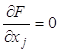 ,
, ![]() (
(![]() ),
), ![]() .
.
Вспомним критерий, позволяющий определить: является ли квадратичная форма и матрица, ее представляющая, положительно определенной, или отрицательно определенной.
3. Критерий Сильвестра
Позволяет ответить на вопрос: является ли квадратичная форма и матрица, ее представляющая, положительно определенной, или отрицательно определенной.
Далее изложение будет относительно ДКФ и матрицы ![]() ее определяющей, т.е. ДКФ вида
ее определяющей, т.е. ДКФ вида
![]() .
.
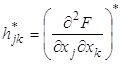 ,
, ![]() - называется матрицей Гессе.
- называется матрицей Гессе.
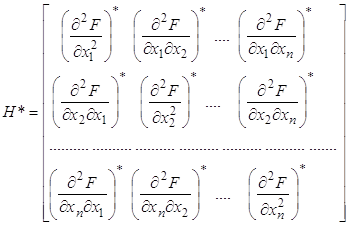
Главный определитель матрицы Гессе ![]()
![]()
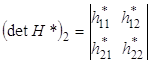
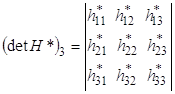
![]()
![]() и ДКФ, которую оно представляет, будут положительно определенными, если все главные определители матрицы Гессе (
и ДКФ, которую оно представляет, будут положительно определенными, если все главные определители матрицы Гессе (![]() ) положительны (т.е. имеет место следующая схема знаков:
) положительны (т.е. имеет место следующая схема знаков:
![]() )
)
Если же имеет место другая схема знаков для главных определителей матрицы Гессе ![]() , например,
, например, ![]() , то матрица
, то матрица ![]() и ДКФ отрицательно определены.
и ДКФ отрицательно определены.
Похожие работы
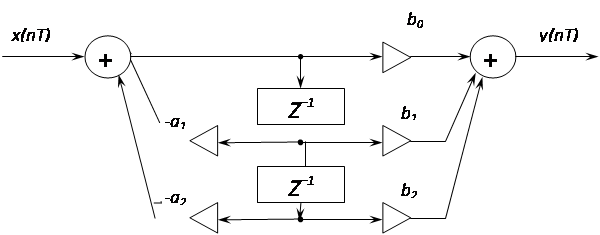
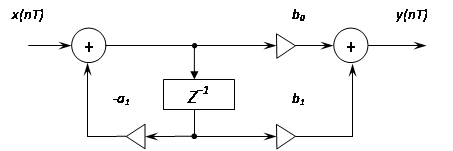
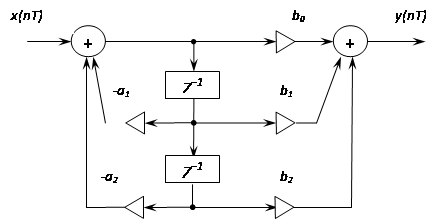
... звеньев первого и второго порядка представлена на следующем рисунке: 3. Методы расчета БИХ-фильтров и вид целевой функции Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях. ...
... лицу на основе договора доверительного управления имуществом*. С помощью такого договора (траста) можно управлять фондовым портфелем промышленных акционерных обществ, инвестиционных компаний и фондов. 5. Оценка инвестиционной привлекательности ценных бумаг акционерного общества (эмитента) Цель инвестирования в финансовые активы зависит от предпочтений каждого вкладчика. Классический вариант ...
... . 1.3 Законы памяти Какие же закономерности восприятия, хранения и воспроизведения информации отмечены исследователями механизмов памяти. 1.3.1 Опора на эмоции На свойства память весьма значительное влияние оказывают эмоции, и это необходимо учитывать в процессе работы по улучшению памяти. Нужно получить глубокое, точное, яркое впечатление о том, что необходимо запомнить. Как ...
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...

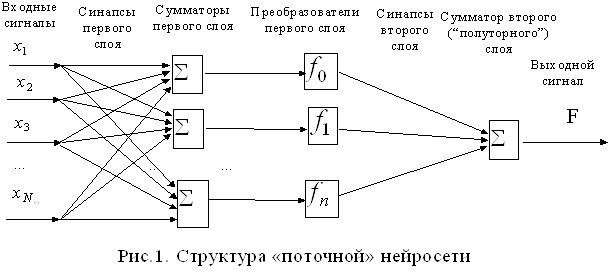

0 комментариев