Навигация
Достаточные условия в классической задаче условной оптимизации. Алгоритм ММЛ
5.3 Достаточные условия в классической задаче условной оптимизации. Алгоритм ММЛ
Эти условия позволяют выяснить, является ли условно-стационарная точка ![]() точкой локального условного минимума, или точкой локального условного максимума.
точкой локального условного минимума, или точкой локального условного максимума.
Относительно просто, подобно тому, как были получены достаточные условия в задаче на безусловный экстремум. Можно получить достаточные условия и в задаче классической условной оптимизации.
Результат этого исследования:
![]()
где ![]() - точка локального условного минимума.
- точка локального условного минимума.
![]()
где ![]() - точка локального условного максимума,
- точка локального условного максимума, ![]() - матрица Гессе с элементами
- матрица Гессе с элементами
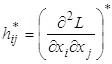 ,
, ![]()
Матрица Гессе ![]() имеет размерность
имеет размерность ![]() .
.
Размерность матрицы Гессе ![]() можно уменьшить, используя условие неравенства нулю якобиана:
можно уменьшить, используя условие неравенства нулю якобиана: ![]() . При этом условии можно зависимые переменные
. При этом условии можно зависимые переменные ![]() выразить через независимые переменные
выразить через независимые переменные ![]() , тогда матрица Гессе будет иметь размерность
, тогда матрица Гессе будет иметь размерность ![]() , т.е. необходимо говорить о матрице
, т.е. необходимо говорить о матрице ![]() с элементами
с элементами
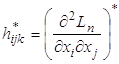 ,
, ![]()
тогда достаточные условия будут иметь вид:
![]() ,
, ![]() - точка локального условного минимума.
- точка локального условного минимума.
![]() ,
, ![]() - точка локального условного максимума.
- точка локального условного максимума.
Доказательство: Алгоритм ММЛ:
1) составляем функцию Лагранжа: ![]() ;
;
2) используя необходимые условия, формируем систему уравнений:

3) из решения этой системы находим точку ![]() ;
;
4) используя достаточные условия, определяем, является ли точка ![]() точкой локального условного минимума или максимума, затем находим
точкой локального условного минимума или максимума, затем находим
![]()
1.5.4. Графо-аналитический метод решения классической задачи условной оптимизации в пространстве ![]() и его модификации при решении простейших задач ИП и АП
и его модификации при решении простейших задач ИП и АП
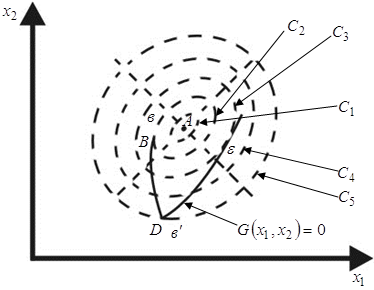
Этот метод использует геометрическую интерпретацию классической задачи условной оптимизации и основан на ряде важных фактов, присущих этой задаче.
![]() ;
; ![]() ;
; ![]() ;
;
![]()
![]()
В ![]() - общая касательная для функции
- общая касательная для функции ![]() и функции
и функции ![]() , представляющей ОДР
, представляющей ОДР ![]() .
.
Как видно из рисунка точка ![]() - точка безусловного минимума, точка
- точка безусловного минимума, точка ![]() точка условного локального минимума, точка
точка условного локального минимума, точка ![]() - точка условного локального максимума.
- точка условного локального максимума.
Докажем, что в точках условных локальных экстремумов кривая ![]() и соответствующие линии уровня
и соответствующие линии уровня
![]() ;
; ![]() .
.
Из курса МА известно, что в точке касания выполняется условие
![]()
где ![]() - угловой коэффициент касательной, проведенной соответствующей линией уровня;
- угловой коэффициент касательной, проведенной соответствующей линией уровня; ![]() - угловой коэффициент касательной, проведенной к функции
- угловой коэффициент касательной, проведенной к функции
![]()
Известно выражение (МА) для этих коэффициентов:
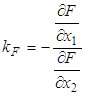 ;
; 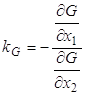
Докажем, что эти коэффициенты равны.

![]() ;
; ![]()
потому что об этом "говорят" необходимые условия

![]() .
.
Вышесказанное позволяет сформулировать алгоритм ГФА метода решения классической задачи условной оптимизации:
1) строим семейство линий уровня целевой функции:
![]() ;
; ![]() ;
;
2) строим ОДР, используя уравнение ограничения
![]()
3) с целью внесения исправления возрастания функции ![]() , находим
, находим ![]() и выясняем характер экстремальных точек;
и выясняем характер экстремальных точек;
4) исследуем взаимодействие линий уровня и функции ![]() , находя при этом из системы уравнений
, находя при этом из системы уравнений 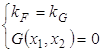 координаты условно стационарных точек – локальных условных минимумов и локальных условных максимумов.
координаты условно стационарных точек – локальных условных минимумов и локальных условных максимумов.
5) вычисляем
![]()
Следует особо отметить, что основные этапы ГФА метода решения классической задачи условной оптимизации совпадают с основными этапами ГФА метода решения задач НП и ЛП, отличие лишь в ОДР ![]() , а также в нахождении местоположения экстремальных точек в ОДР (например, в задачах ЛП эти точки обязательно находятся в вершинах выпуклого многоугольника, представляющего ОДР
, а также в нахождении местоположения экстремальных точек в ОДР (например, в задачах ЛП эти точки обязательно находятся в вершинах выпуклого многоугольника, представляющего ОДР ![]() ).
).
Похожие работы
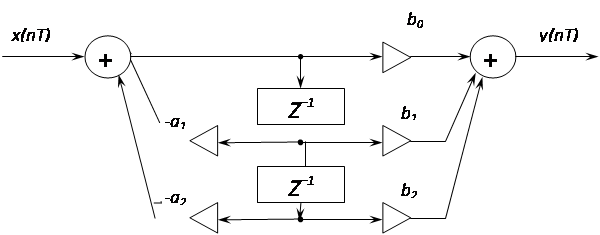
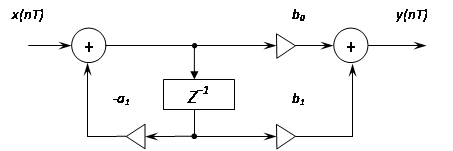
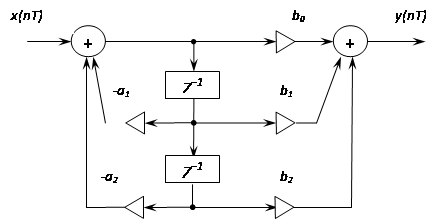
... звеньев первого и второго порядка представлена на следующем рисунке: 3. Методы расчета БИХ-фильтров и вид целевой функции Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях. ...
... лицу на основе договора доверительного управления имуществом*. С помощью такого договора (траста) можно управлять фондовым портфелем промышленных акционерных обществ, инвестиционных компаний и фондов. 5. Оценка инвестиционной привлекательности ценных бумаг акционерного общества (эмитента) Цель инвестирования в финансовые активы зависит от предпочтений каждого вкладчика. Классический вариант ...
... . 1.3 Законы памяти Какие же закономерности восприятия, хранения и воспроизведения информации отмечены исследователями механизмов памяти. 1.3.1 Опора на эмоции На свойства память весьма значительное влияние оказывают эмоции, и это необходимо учитывать в процессе работы по улучшению памяти. Нужно получить глубокое, точное, яркое впечатление о том, что необходимо запомнить. Как ...
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...

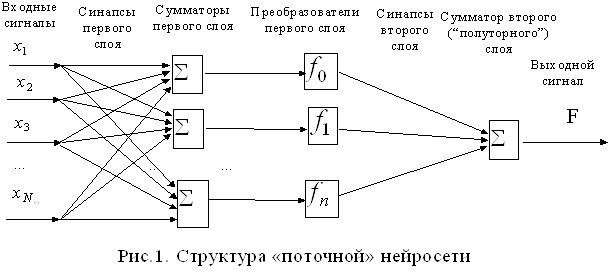

0 комментариев