Навигация
Метод Эйлера – классический метод решения задач безусловной оптимизации
4. Метод Эйлера – классический метод решения задач безусловной оптимизации
Этот метод основан на необходимых и достаточных условиях, изученных в 1.1 – 1.3; применим нахождению локальных экстремумов только непрерывных дифференцируемых функций.
Алгоритм этого метода достаточно прост:
1) используя необходимые условия формируем систему ![]() в общем случае нелинейных уравнений. Отметим, что решить аналитически эту систему в общем случае невозможно; следует применить численные методы решения систем нелинейных уравнений (НУ) (см. "ЧМ"). По этой причине метод Эйлера будет аналитически-численным методом. Решая указанную систему уравнений находим координаты стационарной точки
в общем случае нелинейных уравнений. Отметим, что решить аналитически эту систему в общем случае невозможно; следует применить численные методы решения систем нелинейных уравнений (НУ) (см. "ЧМ"). По этой причине метод Эйлера будет аналитически-численным методом. Решая указанную систему уравнений находим координаты стационарной точки ![]() .;
.;
2) исследуем ДКФ и матрицу Гессе ![]() , которая ее представляет. С помощью критерия Сильвестра определяем, является ли стационарная точка
, которая ее представляет. С помощью критерия Сильвестра определяем, является ли стационарная точка ![]() точкой минимума или точкой максимума;
точкой минимума или точкой максимума;
3) вычисляем значение целевой функции ![]() в экстремальной точке
в экстремальной точке
![]()
Методом Эйлера решить следующую задачу безусловной оптимизации: найти 4 стационарные точки функции вида:
![]()
Выяснить характер этих точек, являются ли они точками минимума, или Седловыми (см. [3]). Построить графическое отображение этой функции в пространстве и на плоскости (с помощью линий уровня).
Далее эту функцию будем именовать типовой функцией, исследуя ее экстремальные свойства всеми изученными методами.
5. Классическая задача условной оптимизации и методы ее решения: Метод исключения и Метод множителей Лагранжа (ММЛ)
Как известно, классическая задача условной оптимизации имеет вид:
![]() (1)
(1)
![]() (2)
(2)
График, поясняющий постановку задачи (1), (2) в пространстве ![]() .
.
![]() (1')
(1')
![]() (2')
(2')
![]() ,
, ![]()
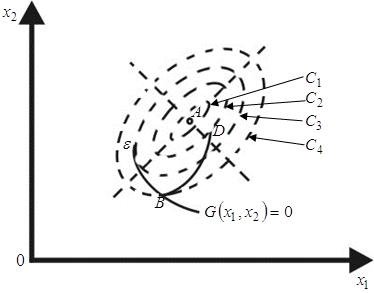
![]() - уравнения линий уровня
- уравнения линий уровня
Итак, ОДР ![]() в рассматриваемой задаче представляет собой некоторую кривую, представленную уравнением (2').
в рассматриваемой задаче представляет собой некоторую кривую, представленную уравнением (2').
Как видно из рисунка, точка ![]() является точкой безусловного глобального максимума; точка
является точкой безусловного глобального максимума; точка ![]() - точкой условного (относительного) локального минимума; точка
- точкой условного (относительного) локального минимума; точка ![]() - точка условного (относительного) локального максимума.
- точка условного (относительного) локального максимума.
Задачу (1'), (2') можно решить методом исключения (подстановки), решив уравнение (2') относительно переменной ![]() , и подставляя найденное решение (1').
, и подставляя найденное решение (1').
![]()
Исходная задача (1'), (2') таким образом преобразована в задачу безусловной оптимизации функции ![]() , которую легко решить методом Эйлера.
, которую легко решить методом Эйлера.
Метод исключения (подстановки).
Пусть целевая функция зависит от ![]() переменных:
переменных:
![]()
![]()
называются зависимыми переменными (или переменными состояния); соответственно можно ввести вектор
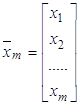
Оставшиеся ![]() переменных
переменных ![]() называются независимыми переменными решения.
называются независимыми переменными решения.
Соответственно можно говорить о вектор-столбце:
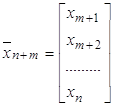 и вектора
и вектора 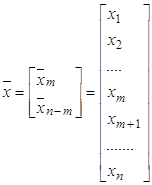 .
.
В классической задаче условной оптимизации:
![]() (1)
(1)
![]() (2)
(2)
Система (2) в соответствии с методом исключения (подстановки) должна быть разрешена относительно зависимых переменных (переменных состояния), т.е. должны быть получены следующие выражения для зависимых переменных:
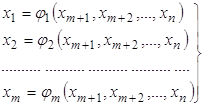 (3)
(3)
Всегда ли система уравнений (2) разрешима относительно зависимых переменных ![]() - не всегда, это возможно лишь в случае, когда определитель
- не всегда, это возможно лишь в случае, когда определитель ![]() , называемый якобианом, элементы которого имеют вид:
, называемый якобианом, элементы которого имеют вид:
![]() ,
, ![]()
не равен нулю (см. соответствующую теорему в курсе МА)
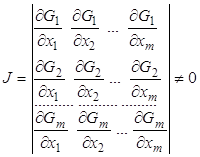
Как видно, функции ![]() ,
, ![]() должны быть непрерывными дифференцируемыми функциями, во-вторых, элементы определителя
должны быть непрерывными дифференцируемыми функциями, во-вторых, элементы определителя ![]() должны быть вычислены в стационарной точке целевой функции.
должны быть вычислены в стационарной точке целевой функции.
Подставляем ![]() из (3) в целевую функцию (1), имеем:
из (3) в целевую функцию (1), имеем:
![]()
![]() (5)
(5)
Исследуемая функция ![]() на экстремум можно произвести методом Эйлера – методом безусловной оптимизации непрерывно дифференцируемой функции.
на экстремум можно произвести методом Эйлера – методом безусловной оптимизации непрерывно дифференцируемой функции.
Итак, метод исключения (подстановки) позволяет использовать задачу классической условной оптимизации преобразовать в задачу безусловной оптимизации функции ![]() - функции
- функции ![]() переменных при условии (4), позволяющим получить систему выражений (3).
переменных при условии (4), позволяющим получить систему выражений (3).
Недостаток метода исключения: трудности, а иногда и невозможность получения системы выражений (3). Свободный от этого недостатка, но требующий выполнения условия (4) ![]() является ММЛ.
является ММЛ.
5.2. Метод множителей Лагранжа. Необходимые условия в классической задаче условной оптимизации. Функция Лагранжа ![]()
ММЛ позволяет исходную задачу классической условной оптимизации:
![]() (1)
(1)
![]() (2)
(2)
Преобразовать в задачу безусловной оптимизации специально сконструированной функции – функции Лагранжа:
 , (3)
, (3)
где ![]() ,
, ![]() - множители Лагранжа;
- множители Лагранжа;
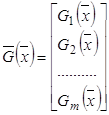 .
.
Как видно, ![]() представляет собой сумму, состоящую из исходной целевой функции
представляет собой сумму, состоящую из исходной целевой функции ![]() и "взвешенной" суммы функций
и "взвешенной" суммы функций ![]() ,
, ![]() - функции, представляющие их ограничения (2) исходной задачи.
- функции, представляющие их ограничения (2) исходной задачи.
Пусть точка ![]() - точка безусловного экстремума функции
- точка безусловного экстремума функции ![]() , тогда, как известно,
, тогда, как известно, 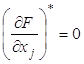 ,
, ![]() , или
, или ![]() (полный дифференциал функции
(полный дифференциал функции ![]() в точке
в точке ![]() ).
).
Используя концепция зависимых и независимых переменных ![]() - зависимые переменные;
- зависимые переменные; ![]() - независимые переменные, тогда представим (5) в развернутом виде:
- независимые переменные, тогда представим (5) в развернутом виде:
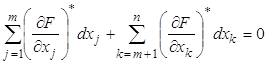 (5')
(5')
Из (2) с очевидностью следует система уравнений вида:
![]() ,
, ![]() (6)
(6)
Результат вычисления полного дифференциала для каждой из функций
![]()
Представим (6) в "развернутом" виде, используя концепцию зависимых и независимых переменных:
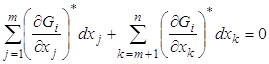 ,
, ![]() (6')
(6')
Заметим, что (6') в отличии от (5') представляет собой систему, состоящую из ![]() уравнений.
уравнений.
Умножим каждое ![]() -ое уравнение системы (6') на соответствующий
-ое уравнение системы (6') на соответствующий ![]() -ый множитель Лагранжа. Сложим их между собой и с уравнением (5') и получим выражение:
-ый множитель Лагранжа. Сложим их между собой и с уравнением (5') и получим выражение:
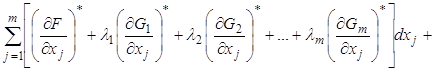
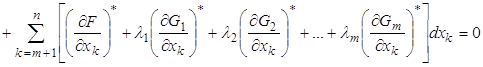 (7)
(7)
Распорядимся множителями Лагранжа ![]() таким образом, чтобы выражение в квадратных скобках под знаком первой суммы (иными словами, коэффициенты при дифференциалах независимых переменных
таким образом, чтобы выражение в квадратных скобках под знаком первой суммы (иными словами, коэффициенты при дифференциалах независимых переменных ![]() ,
, ![]() ) равнялось нулю.
) равнялось нулю.
Термин "распорядимся" множителями Лагранжа вышеуказанным образом означает, что необходимо решить некоторую систему из ![]() уравнений относительно
уравнений относительно ![]() .
.
Структуру такой системы уравнений легко получить приравняв выражение в квадратной скобке под знаком первой суммы нулю:
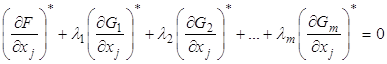 ,
, ![]() (8)
(8)
Перепишем (8) в виде
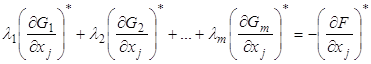 ,
, ![]() (8')
(8')
Система (8') представляет собой систему из ![]() линейных уравнений относительно
линейных уравнений относительно ![]() известных:
известных: ![]() . Система разрешима, если
. Система разрешима, если ![]() (вот почему, как и в методе исключения в рассматриваемом случае должно выполняться условие
(вот почему, как и в методе исключения в рассматриваемом случае должно выполняться условие ![]() ). (9)
). (9)
Поскольку в ключевом выражении (7) первая сумма равна нулю, то легко понять, что и вторая сумма будет равняться нулю, т.е. имеет место следующая система уравнений:
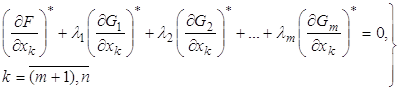 (10)
(10)
Система уравнений (8) состоит из ![]() уравнений, а система уравнений (10) состоит из
уравнений, а система уравнений (10) состоит из ![]() уравнений; всего
уравнений; всего ![]() уравнений в двух системах, а неизвестных
уравнений в двух системах, а неизвестных
![]() :
: ![]() ,
, ![]()
Недостающие ![]() уравнений дает система уравнений ограничений (2):
уравнений дает система уравнений ограничений (2):
![]() ,
, ![]()
Итак, имеется система из ![]() уравнений для нахождения
уравнений для нахождения ![]() неизвестных:
неизвестных:
 (11)
(11)
Полученный результат – система уравнений (11) составляет основное содержание ММЛ.
Легко понять, что систему уравнений (11) можно получить очень просто, вводя в рассмотрение специально сконструированную функцию Лагранжа (3).
Действительно
 ,
, ![]() (12)
(12)
![]() ,
, ![]() (13)
(13)
Итак, система уравнений (11) представима в виде (используя (12), (13)):
 (14)
(14)
Система уравнений (14) представляет необходимое условие в классической задаче условной оптимизации.
Найденное в результате решение этой системы значение вектора ![]() называется условно-стационарной точкой.
называется условно-стационарной точкой.
Для того, чтобы выяснить характер условно-стационарной точки ![]() необходимо воспользоваться достаточными условиями.
необходимо воспользоваться достаточными условиями.
Похожие работы
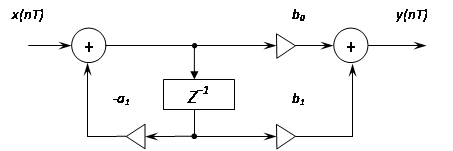
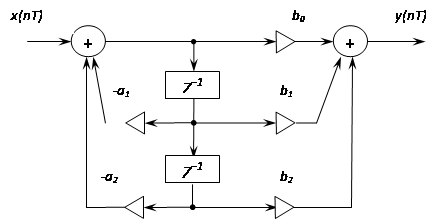
... звеньев первого и второго порядка представлена на следующем рисунке: 3. Методы расчета БИХ-фильтров и вид целевой функции Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях. ...
... лицу на основе договора доверительного управления имуществом*. С помощью такого договора (траста) можно управлять фондовым портфелем промышленных акционерных обществ, инвестиционных компаний и фондов. 5. Оценка инвестиционной привлекательности ценных бумаг акционерного общества (эмитента) Цель инвестирования в финансовые активы зависит от предпочтений каждого вкладчика. Классический вариант ...
... . 1.3 Законы памяти Какие же закономерности восприятия, хранения и воспроизведения информации отмечены исследователями механизмов памяти. 1.3.1 Опора на эмоции На свойства память весьма значительное влияние оказывают эмоции, и это необходимо учитывать в процессе работы по улучшению памяти. Нужно получить глубокое, точное, яркое впечатление о том, что необходимо запомнить. Как ...
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...


0 комментариев