Краткие теоретические сведения
Анализ объектов
Анализ нелинейных стационарных объектов
Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона
Последовательность выполнения работы
Краткие теоретические положения
Численные методы решения обыкновенных дифференциальных уравнений
Навигация
Краткие теоретические сведения
Анализ линейных стационарных объектов
34983
знака
6
таблиц
8
изображений
1.1. Краткие теоретические сведения
1.1.1. Иерархические уровни описания объектов
Описания технических объектов должны быть по сложности согласованы с возможностями восприятия человеком и возможностями оперирования описаниями в процессе их преобразования с помощью имеющихся средств проектирования. Однако выполнить это требование в рамках некоторого единого описания, не разделяя его на некоторые составные части, удается лишь для простых изделий. Как правило, требуется структурирование описаний и соответствующее разделение представлений о проектируемых объектах на иерархические уровни и аспекты.
Разделение описаний по степени детализации отображаемых свойств и характеристик объекта лежит в основе блочно-иерархического подхода к проектированию и приводит к появлению иерархических уровней в представлениях о проектируемом объекте.
На каждом иерархическом уровне используются свои понятия системы и элементов.
На уровне 1 (верхнем уровне) подлежащий проектированию сложный объект S рассматривается как система S из n взаимосвязанных и взаимодействующих элементов
Среди свойств объекта, отражаемых в описаниях на определенном иерархическом уровне, различают свойства систем, элементов систем и внешней среды, в которой должен функционировать объект. Количественное выражение этих свойств осуществляется с помощью величин, называемых параметрами. Величины, характеризирующие свойства системы, элементов системы и внешней среды, называют соответственно выходными, внутренними и внешними параметрами. Например, для электронного усилителя выходными параметрами являются полоса пропускания, коэффициент усиления; внутренними параметрами – сопротивления резисторов, емкости конденсаторов, параметры транзисторов; внешними параметрами – сопротивление и емкость нагрузки, напряжение источников питания.
Обозначим количества выходных Si. Каждый из элементов в описании уровня 1 представляет собой сложный объект, который, в свою очередь, рассматривается как система Si на уровне 2. Элементами систем Si являются объекты Sij, где j=1,2…, mi (mi– количество элементов в описании системы Si). Подобное разделение продолжается вплоть до получения на некотором уровне элементов, описания которых дальнейшему делению не подлежат. Такие элементы по отношению к объекту S называют базовыми элементами.
1.1.2. Классификация параметров объектов
Внутренних и внешних параметров через m, n, l, а векторы этих параметров соответственно через Y=(y1,y2,…,ym), X=(x1,x2,…,xn), Q=(q1,q2,…,ql). Свойства системы зависят от внутренних и внешних параметров, т.е. имеет место функциональная зависимость:
Y=F(X,Q). (1.1)
1.1.3. Структура и математическая модель объекта
Структура объекта – это перечень типов элементов, составляющих объект, и способа связи элементов между собой в составе объекта.
Математическая модель (ММ) технического объекта – это система математических объектов (чисел, переменных, матриц, множеств и т.п.) и отношений между ними, отражающая некоторые свойства технического объекта. Наличие ММ позволяет легко оценивать выходные параметры по известным значениям векторов X и Q. Такая система соотношений (1) является примером математической модели объекта. Однако, существование зависимости (1.1) не означает, что она известна разработчикам и может быть представлена именно в таком явном относительно вектора Y виде. Как правило, ММ в виде (1.1) удается получить только для очень простых объектов. Типичной является ситуация, когда математическое описание процессов в проектируемом объекте задается моделью в форме системы уравнений.
Ряд технических объектов в установившемся (стационарном) состоянии (режиме) может быть описан системами линейных алгебраических уравнений.
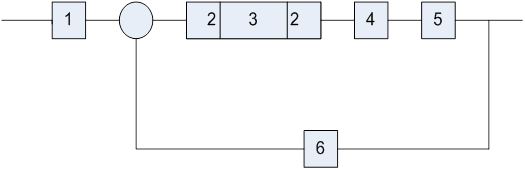
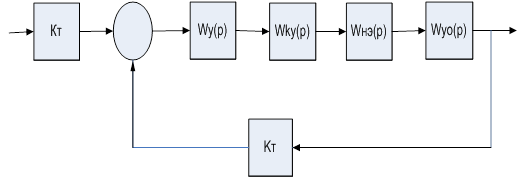
Такого рода объекты (например, объект, показанный на рис 1.1) относятся к классу линейных стационарных объектов.
|
|
|
|
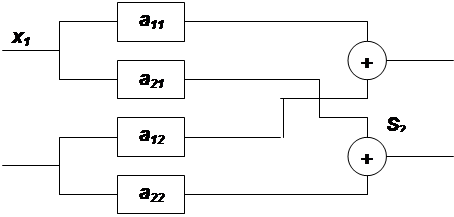
Рис. 1.1. Структура линейного стационарного объекта
Структура данного объекта определяется двумя сумматорами S1 и S2, четырьмя линейно– усилительными блоками а11, а12, а21, а22и системой связей между ними.
Математическая модель такого рода объекта представляет собой систему линейных алгебраических уравнений и имеет вид:
а11х1 +а12х2=в1;
а21х1 +а22х2=в2;
Похожие работы
уле . Т.о. имеем: Минимальная энергия: Найдем управление по следующей формуле: Тогда оптимальное управление . 3.2 Оптимальная L – проблема моментов в пространстве состояний Система задана в виде: Решение ДУ имеет вид: , при имеем: . Составим моментные уравнения: Подставляя необходимые данные в выше приведенные формулы, получим следующие ...
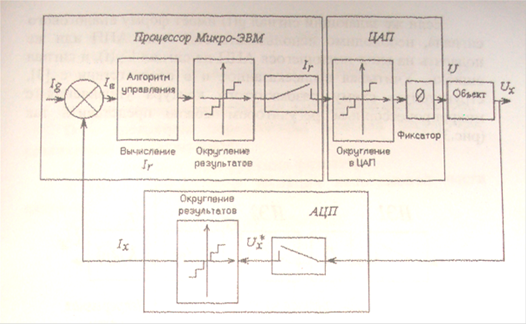
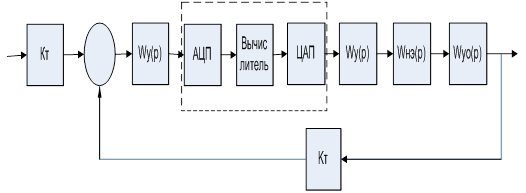
... , Полученные данные будут составлять так называемую неизменяемую часть системы. Получим, что передаточная функция такой неизменяемой части системы имеет вид 2. Структурная схема САУ с микропроцессорным регулятором Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал Ur - ...
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... , на нерегулируемые его влияние не распространяется. Учет по центрам ответственности позволяет оценить деятельность подразделения и его руководителя, обеспечивает оперативный учет, анализ и контроль, а также предоставление информации о затратах. Задачи анализа затрат на качество обусловливают введение двух отчетных форм: - сводный отчет о затратах на качество, содержащий полную информацию о ...
0 комментариев