Краткие теоретические сведения
Анализ объектов
Анализ нелинейных стационарных объектов
Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона
Последовательность выполнения работы
Краткие теоретические положения
Численные методы решения обыкновенных дифференциальных уравнений
Навигация
Последовательность выполнения работы
Анализ линейных стационарных объектов
34983
знака
6
таблиц
8
изображений
2.2. Последовательность выполнения работы
Согласно номеру по списку группы выбрать из табл.2.1 значения параметров для нелинейного объекта. По формулам
в1і= в1–h(і-1) ;
в2і= в2–h(і-1) ;
для і=1,2,...5 определить значения коэффициентов, определяющих выход для пяти рассматриваемых случаев.
2. Составить и отладить программу решения системы нелинейных уравнений согласно Приложению 2.1 и для полученных в пункте 1 значений выхода найти пять наборов значений входных переменных х1 и х2 .
3. По результатам просчета на ПЭВМ получить таблицы значений входа (х1 и х2 ) при заданных значениях выхода ( в1 и в2).
4. Построить графики изменения значений х1 и х2в зависимости от значений в1 и в2. .
Таблица 2.1
| Номер по списку | Задания Коэффициенты системы уравнений а1 х1+ а2 х2=в1; х1 х2=в2; а1 а2 в1 в2 h |
| 1 | 1 2 4 2 0.1 |
| 2 | 2 1 3 1 |
| 3 | 1 2 3 1 |
| 4 | 2 2 4 1 |
| 5 | 2 1 4 2 |
| 6 | 1 3 4 1 |
| 7 | 1 1 5 3 |
| 8 | 1 3 5 2 |
| 9 | 3 3 6 1 |
| 10 | 2 3 7 2 |
| 11 | 3 3 9 2 |
| 12 | 2 2 9 2 |
| 13 | 1 1 9 2 |
| 14 | 1 3 5 2 |
| 15 | 1 1 7 3 |
| 16 | 2 2 7 3 |
| 17 | 2 3 5 1 |
| 18 | 3 1 5 2 |
| 19 | 5 5 10 1 |
| 20 | 6 2 10 2 |
| 21 | 2 2 10 2 |
| 22 | 1 1 10 2 |
| 23 | 1 1 11 2 |
| 24 | 2 2 11 2 |
| 25 | 2 2 11 3 |
| 26 | 2 2 11 4 |
| 27 | 2 2 11 5 |
| 28 | 2 2 11 6 |
| 29 | 2 2 11 7 |
| 30 | 1 1 11 8 |
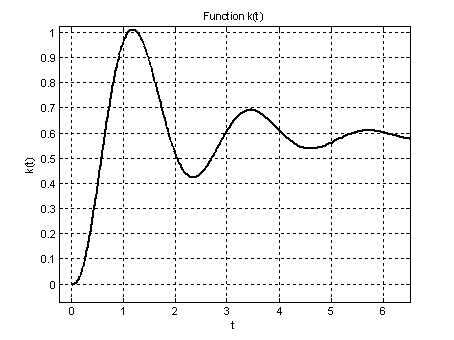
3. Анализ динамических объектов
Цель работы: исследовать свойства и поведение динамических объектов, описываемых системами обыкновенных нелинейных дифференциальных уравнений, используя для их решения средства пакета MathCAD.
Содержание работы:
1) изучить теоретические положения (раздел 3.1), определяющие структуру динамических объектов, их математическое описание и решение задачи анализа объектов, методы решения обыкновенных дифференциальных уравнений и систем уравнений;
2) выполнить индивидуальное задание согласно предусмотренной в разд.3.2 последовательности выполнения работы;
3) оформить описание контрольной работы согласно требованиям задания.
Похожие работы
уле . Т.о. имеем: Минимальная энергия: Найдем управление по следующей формуле: Тогда оптимальное управление . 3.2 Оптимальная L – проблема моментов в пространстве состояний Система задана в виде: Решение ДУ имеет вид: , при имеем: . Составим моментные уравнения: Подставляя необходимые данные в выше приведенные формулы, получим следующие ...
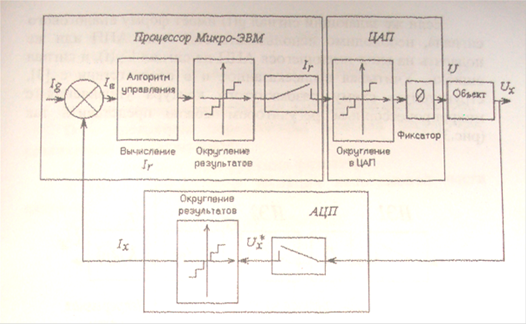
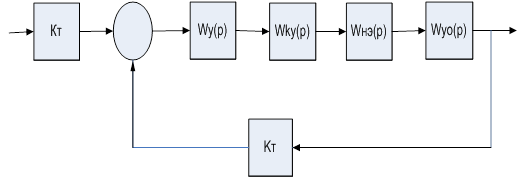
... , Полученные данные будут составлять так называемую неизменяемую часть системы. Получим, что передаточная функция такой неизменяемой части системы имеет вид 2. Структурная схема САУ с микропроцессорным регулятором Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал Ur - ...
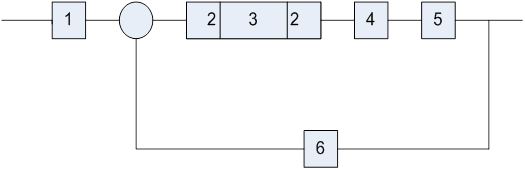
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... , на нерегулируемые его влияние не распространяется. Учет по центрам ответственности позволяет оценить деятельность подразделения и его руководителя, обеспечивает оперативный учет, анализ и контроль, а также предоставление информации о затратах. Задачи анализа затрат на качество обусловливают введение двух отчетных форм: - сводный отчет о затратах на качество, содержащий полную информацию о ...
0 комментариев