Краткие теоретические сведения
Анализ объектов
Анализ нелинейных стационарных объектов
Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона
Последовательность выполнения работы
Краткие теоретические положения
Численные методы решения обыкновенных дифференциальных уравнений
Навигация
Краткие теоретические положения
Анализ линейных стационарных объектов
34983
знака
6
таблиц
8
изображений
3.1. Краткие теоретические положения
3.1.1. Структура и математическая модель объекта
В общем случае под динамическими (нестационарными) объектами понимают такие объекты, состояние и поведение которых определяется временными характеристиками, т.е. является функцией времени.
Такого рода объекты могут быть описаны системами нелинейных дифференциальных уравнений вида 
где 
– функционал, определяющий конкретный вид системы уравнений, которая описывает структуру объекта; 
– вектор переменных, описывающий выходы объекта; 
– вектор производных; 
– вектор внутренних параметров уравнения, определяющий конкретную реализацию объекта при заданной его структуре; 
– внешние (входные) воздействия на объект.
Системе уравнений вида:
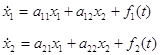
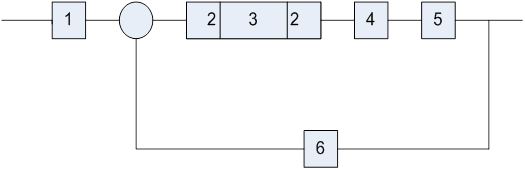
будет соответствовать структура объекта, изображенного на рис 3.1.
Структура объекта определяется интеграторами И1 и И2 , сумматорами S1, S2, S3, и S4, линейно– усилительными блоками а11, а12,а21,а22и системой связей между ними.
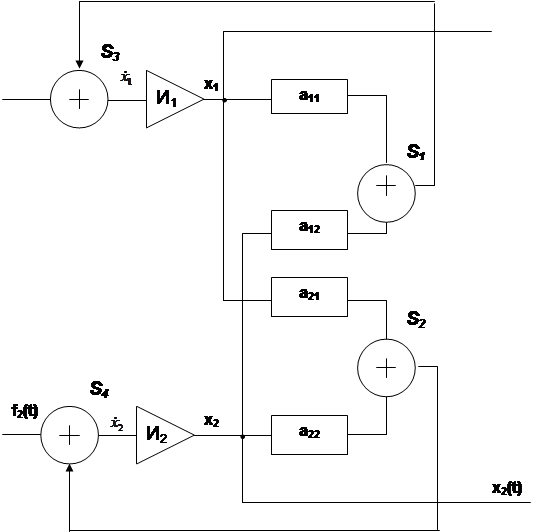
Рис 3.1. Структура динамического объекта.
3.1.2. Анализ динамических объектов
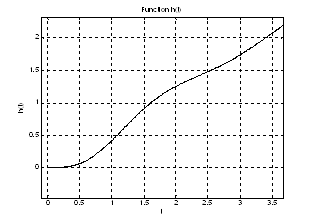
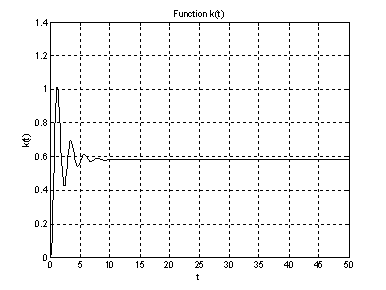
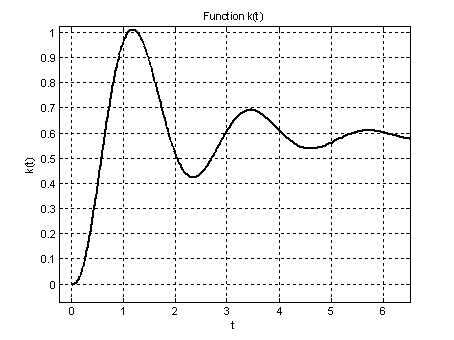
Задача анализа динамических объектов состоит в исследовании зависимости выходных значений объекта х1(t) и х2(t) как функции времени при заданных внешних (входных) воздействиях на объект f1(t) и f2 (t) и внутренних параметрах объекта а11, а12,а21,а22 .
Решение задачи анализа состоит в динамическом моделировании объекта, который описывается системой обыкновенных дифференциальных уравнений, и заключается в решении (интегрировании) системы уравнений на интервале времени. Этот интервал времени (от 
– начального до 
– конечного) называется интервалом интегрирования. В большинстве практических случаев равно нулю, то есть моделирование начинается в нулевой момент времени. В описании такого рода систем переменная 
называется независимой, а все остальные переменные – зависимыми.
3.1.3. Решение обыкновенных дифференциальных уравнений
Дифференциальными называются уравнения, содержащие одну или несколько производных. В зависимости от числа независимых переменных, и, следовательно, типа входящих в них производных, дифференциальные уравнения делятся на две категории:
обыкновенные дифференциальные уравнения (ОДУ), содержащие одну независимую переменную и производные по ней;
дифференциальные уравнения в частных производных (ДУЧП), содержащие несколько независимых переменных и производных по ним, которые называются частными производными.
Для решения дифференциальных уравнений могут применяться различного рода аналитические и численные методы. Аналитические методы основаны на прямых преобразованиях системы уравнений, приводящих к точному аналитическому решению. Однако такие методы сложны, не универсальны с точки зрения системы уравнений и приводят к решениям только в самых простых случаях. Поэтому они малоприемлемы при решении практических задач.
В последнее время в связи с бурным развитием вычислительной техники широкое применение получили численные методы решения дифференциальных уравнений. В основе этих методов лежит итерационное повторение однотипных вычислительных операций и поэтому они достаточно просто реализуются на ПЭВМ. Эти методы позволяют с заданной точностью находить на интервале интегрирования требуемое количество точек по времени для всех переменных, входящих в систему уравнений.
Среди этих методов можно выделить явные методы (метод Эйлера, метод Рунге–Кутта), простые в реализации. Количество проводимых вычислений для них зависит только от количества переменных и заданного количества точек определения значений переменных на интервале интегрирования. Точность вычисления результатов для этих методов значительно уменьшается при увеличении интервала интегрирования. Лишенной этого недостатка является группа неявных методов (методы прогноза и коррекции), но они обычно превосходят явные по количеству вычислений.
Похожие работы
уле . Т.о. имеем: Минимальная энергия: Найдем управление по следующей формуле: Тогда оптимальное управление . 3.2 Оптимальная L – проблема моментов в пространстве состояний Система задана в виде: Решение ДУ имеет вид: , при имеем: . Составим моментные уравнения: Подставляя необходимые данные в выше приведенные формулы, получим следующие ...
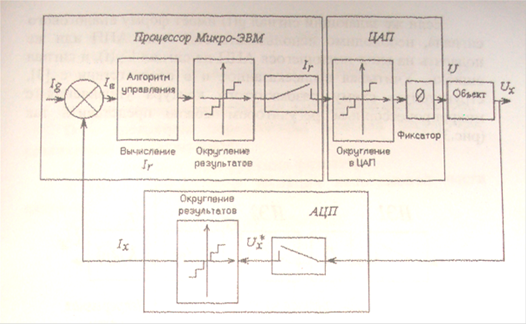
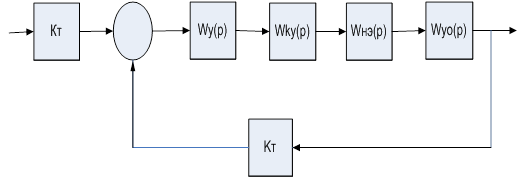
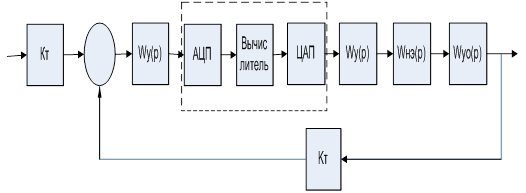
... , Полученные данные будут составлять так называемую неизменяемую часть системы. Получим, что передаточная функция такой неизменяемой части системы имеет вид 2. Структурная схема САУ с микропроцессорным регулятором Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал Ur - ...
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... , на нерегулируемые его влияние не распространяется. Учет по центрам ответственности позволяет оценить деятельность подразделения и его руководителя, обеспечивает оперативный учет, анализ и контроль, а также предоставление информации о затратах. Задачи анализа затрат на качество обусловливают введение двух отчетных форм: - сводный отчет о затратах на качество, содержащий полную информацию о ...
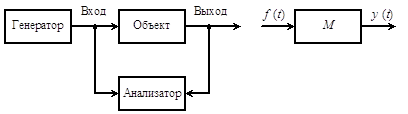
0 комментариев