Краткие теоретические сведения
Анализ объектов
Анализ нелинейных стационарных объектов
Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона
Последовательность выполнения работы
Краткие теоретические положения
Численные методы решения обыкновенных дифференциальных уравнений
Навигация
Анализ объектов
Анализ линейных стационарных объектов
34983
знака
6
таблиц
8
изображений
1.1.4. Анализ объектов
Задача анализа объектов состоит в определении свойств и исследовании работоспособности объекта по его описанию.
При одновариантном анализе задаются значения внутренних и внешних параметров, требуется определить значения выходных параметров объекта.
При одновариантном анализе задается также некоторая точка в пространстве внутренних параметров и требуется в этой точке определить значения выходных параметров. Подобная задача обычно сводится к однократному решению уравнений, составляющих математическую модель, что и обусловливает название этого вида анализа.
Многовариантный анализ заключается в исследовании свойств объекта в некоторой области пространства внутренних параметров. Такой анализ требует многократного решения систем уравнений (многократного выполнения одновариантного анализа).
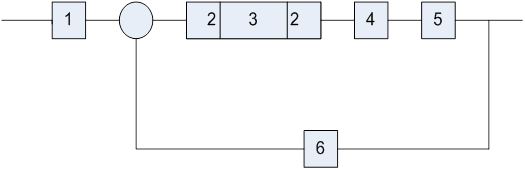
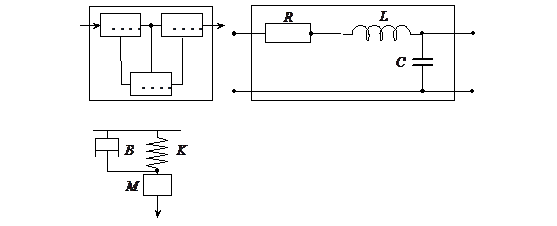
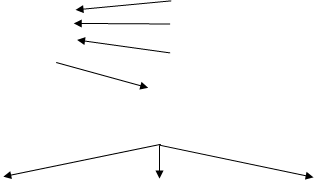
Задача, ставящаяся при анализе (исследовании) такого рода объектов (рис 1.1), может иметь следующий вид: необходимо определить значения входных воздействий х1 и х2при заданной структуре объекта, определяемой системой связей, и заданных значениях внутренних параметров, при которых выход объекта имел бы требуемые выходные значения в1 и в2 .
1.1.5. Решение систем линейных алгебраических уравнений
1.1.5.1. Постановка задачи. Система n линейных алгебраических уравнений (СЛАУ) с n неизвестными
имеет вид:
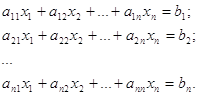(1.2)
– неизвестные числа, подлежащие определению;
– коэффициенты системы;
– свободные члены.
Первый индекс коэффициента указывает номер уравнения, в котором фигурирует данный коэффициент (номер строки), а второй – номер неизвестного, при котором этот коэффициент поставлен (номер столбца). Коэффициенты системы, как и свободные члены, предполагаются известными.
Решением системы (или ее корнями) называется всякая совокупность чисел, 
, которая, будучи подставлена в систему вместо неизвестных , обращает все уравнения системы в тождества. Отметим, что совокупность чисел составляет одно решение системы, а не n решений.
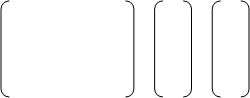
В матричной форме система может быть записана как
(1.3)
или в обобщенной форме:
(1.4)
1.1.5.2. Классификация методов решения. На практике применяют два типа методов:
– прямые или точные;
– итерационные.
Точные – это методы, которые дают решение задачи с помощью конечного числа элементарных арифметических операций. Число необходимых для решения задач вычислительных операций зависит только от вида вычислительной схемы и от порядка матрицы. К точным методам относится метод Гаусса.
Решение СЛАУ итерационными методами получается как предел последовательных приближений, вычисляемых некоторым единообразным процессом. Число арифметических операций в данном случае зависит от вычислительной схемы, порядка матрицы и от требуемой точности. Примером итерационных методов является метод простой итерации.
На практике чаще всего применяются прямые методы (метод Гаусса). Однако, при решении на ЭВМ систем высокого порядка (более 200 уравнений в системе), предпочтительными являются итерационные методы.
Реализация решения задачи анализа линейного стационарного объекта может быть осуществлена с помощью средств матричной алгебры пакета MathCAD.
1.2. Последовательность выполнения работы
1. Согласно номеру варианта (две последние цифры номера зачетной книжки) выбрать из табл.1.1. значения параметров для линейного объекта.
По формулам
в1і= в1+h(і-1) ;
в2і= в2+h(і-1) ;
2. Для і=1,….5 определить значения коэффициентов, определяющих выходные значения объекта для пяти рассматриваемых случаев.
3. Составить и отладить программу решения системы линейных уравнений согласно Приложению 1.1 и для полученных в пункте 2 значений выхода найти пять наборов значений входных переменных х1 и х2 .
4. По результатам просчета на ПЭВМ построить таблицы значений входа (х1 и х2) при заданных значениях выхода ( в1 и в2).
5. Построить графики изменения значений х1 и х2в зависимости от значений в1 и в2.
Таблица 1.1
| Номер варианта | Задания Коэффициенты системы уравнений
a11 a12 a21 a22 b1 b2 h | ||||||
| 1 | 1 | 2 | 3 | 4 | 1 | 2 | 0,1 |
| 2 | 2 | 1 | 4 | 3 | 2 | 1 | |
| 3 | 1 | 1 | 3 | 2 | 3 | 1 | |
| 4 | 3 | 2 | 1 | 1 | 3 | 1 | |
| 5 | 2 | 1 | 1 | 2 | 3 | 2 | |
| 6 | 1 | 2 | 2 | 1 | 2 | 3 | |
| 7 | 4 | 3 | 1 | 2 | 3 | 3 | |
| 8 | 1 | 3 | 3 | 5 | 2 | 2 | |
| 9 | 2 | 3 | 1 | 4 | 1 | 1 | |
| 10 | 2 | 3 | 3 | 2 | 4 | 1 | |
| 11 | 1 | 2 | 2 | 5 | 4 | 3 | |
| 12 | 6 | 3 | 4 | 7 | 4 | 2 | |
| 13 | 1 | 5 | 2 | 3 | 4 | 4 | |
| 14 | 1 | 2 | 3 | 4 | 1 | 4 | |
| 15 | 2 | 3 | 4 | 1 | 2 | 4 | |
| 16 | 3 | 2 | 1 | 4 | 3 | 4 | |
| 17 | 2 | 3 | 1 | 4 | 5 | 1 | |
| 18 | 3 | 1 | 4 | 2 | 5 | 2 | |
| 19 | 1 | 4 | 2 | 3 | 5 | 3 | |
| 20 | 2 | 3 | 2 | 5 | 5 | 4 | |
| 21 | 3 | 2 | 5 | 3 | 4 | 5 | |
| 22 | 4 | 1 | 6 | 2 | 3 | 5 | |
| 23 | 5 | 3 | 4 | 1 | 2 | 5 | |
| 24 | 1 | 4 | 5 | 2 | 1 | 5 | |
| 25 | 1 | 4 | 6 | 2 | 3 | 1 | |
| 26 | 2 | 4 | 5 | 3 | 3 | 2 | |
| 27 | 3 | 4 | 3 | 5 | 1 | 6 | |
| 28 | 3 | 5 | 2 | 1 | 2 | 6 | |
| 29 | 4 | 5 | 1 | 3 | 3 | 6 | |
| 30 | 5 | 4 | 3 | 2 | 6 | 1 | |
Похожие работы
уле . Т.о. имеем: Минимальная энергия: Найдем управление по следующей формуле: Тогда оптимальное управление . 3.2 Оптимальная L – проблема моментов в пространстве состояний Система задана в виде: Решение ДУ имеет вид: , при имеем: . Составим моментные уравнения: Подставляя необходимые данные в выше приведенные формулы, получим следующие ...
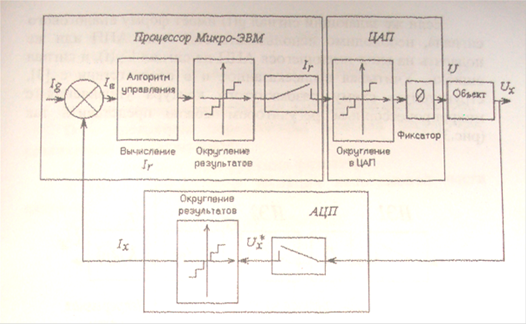
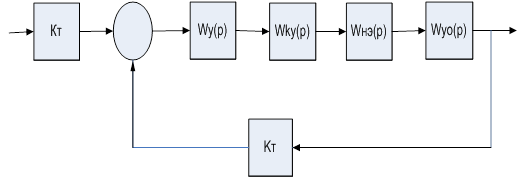
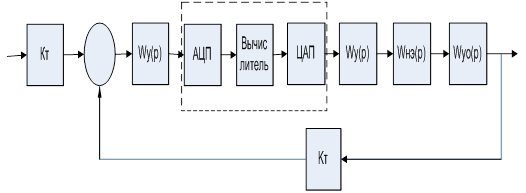
... , Полученные данные будут составлять так называемую неизменяемую часть системы. Получим, что передаточная функция такой неизменяемой части системы имеет вид 2. Структурная схема САУ с микропроцессорным регулятором Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал Ur - ...
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... , на нерегулируемые его влияние не распространяется. Учет по центрам ответственности позволяет оценить деятельность подразделения и его руководителя, обеспечивает оперативный учет, анализ и контроль, а также предоставление информации о затратах. Задачи анализа затрат на качество обусловливают введение двух отчетных форм: - сводный отчет о затратах на качество, содержащий полную информацию о ...
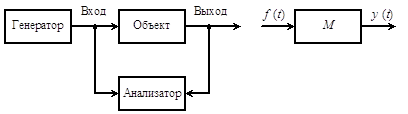
0 комментариев