Навигация
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ТРАЕКТОРИЙ СИСТЕМЫ НА ПЛОСКОСТИ
2 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ТРАЕКТОРИЙ СИСТЕМЫ НА ПЛОСКОСТИ
2.1 Исследование системы (1.1) с коэффициентами, заданными формулами (1.35) в конечной плоскости
Пусть мы имеем систему (1.1), коэффициенты которой определяются согласно формулам (1.35),т.е. систему:
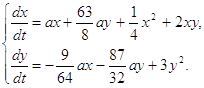 (2.1)
(2.1)
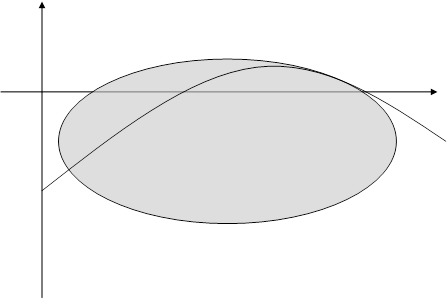
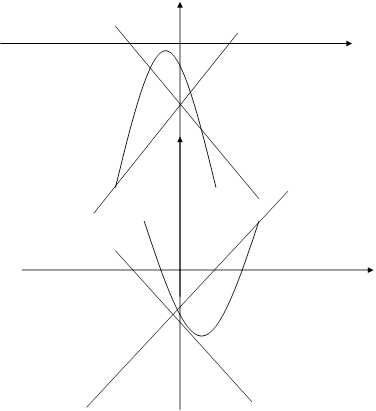
Интегральные кривые (1.4),(1.18), согласно формулам (1.36), имеют вид:
x3+12ax2-![]() axy+ay2+
axy+ay2+![]() a2x-
a2x-![]() a2y+
a2y+![]() a3=0, (2.2)
a3=0, (2.2)
-![]() nx+ny-
nx+ny-![]() an=0. (2.3)
an=0. (2.3)
Найдем состояния равновесия системы (2.1). Приравняв правые части системы к нулю и исключив переменную x, получим следующее уравнение для определения ординат состояний равновесия:
8192y4-11776ay3+5480a2y2-825a3y=0. (2.4)
Из (2.4) получаем, что
y0=0, y1=![]() a, y2=
a, y2=![]() a, y3=
a, y3=![]() a. (2.5)
a. (2.5)
Абсциссы точек покоя имеют вид:
x0=0, x1= -![]() a, x2= -
a, x2= -![]() a, x3= -
a, x3= -![]() a. (2.6)
a. (2.6)
Согласно (2.5) и (2.6) заключаем, что система (2.1) имеет четыре состояния равновесия - ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Исследуем поведение траекторий в окрестностях состояний равновесия ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
1. Исследуем точку ![]() .
.
Составим характеристическое уравнение в точке ![]() [10, с. 1760-1765]
[10, с. 1760-1765]
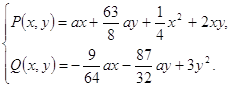
Отсюда ![]()
![]() (2.7)
(2.7)
![]()
![]()
Следовательно, характеристическое уравнение примет вид:
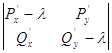 =
=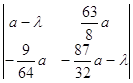 =0.
=0.
![]() ,
,
Характеристическими числами для точки![]() системы (2.1) будут
системы (2.1) будут
![]() .
.
Корни ![]() - действительные, различных знаков не зависимо от параметра a. Следовательно, точка
- действительные, различных знаков не зависимо от параметра a. Следовательно, точка ![]() - седло.
- седло.
2. Исследуем точку ![]() .
.
Составим характеристическое уравнение в точке A. Согласно
равенствам (2.7) характеристическое уравнение примет вид:
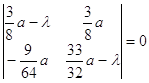
![]() ,
,
![]() ,
,
то есть
![]() ,
, ![]() .
.
Корни ![]() - действительные и одного знака, зависящие от параметра a. Если a<0, то точка
- действительные и одного знака, зависящие от параметра a. Если a<0, то точка ![]() - устойчивый узел, если a>0, то точка
- устойчивый узел, если a>0, то точка ![]() -неустойчивый узел.
-неустойчивый узел.
3. Исследуем точку ![]() .
.
Применяя равенства (2.7), составим характеристическое уравнение в точке B:
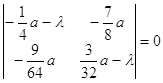
![]()
![]() ,
, ![]() .
.
Корни ![]() - действительные и одного знака. Следовательно, точка
- действительные и одного знака. Следовательно, точка ![]() - седло при любом параметре a .
- седло при любом параметре a .
4. Исследуем точку ![]() .
.
Учитывая выражения (2.7), составим характеристическое уравнение в точке:
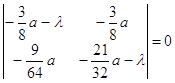
![]() ,
,
Характеристическими числами для точки ![]() системы (2.1) будут
системы (2.1) будут
![]() ,
,
Корни ![]() - действительные и одного знака.Следовательно точка
- действительные и одного знака.Следовательно точка ![]() - устойчивый узел, если a>0 и неустойчивый узел, если a<0 .
- устойчивый узел, если a>0 и неустойчивый узел, если a<0 .
Похожие работы
... в целом выделенных в первом разделе классов систем при фиксированных значениях некоторых параметров. 1. Построение квадратичной двумерной стационарной системы 1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой второго порядка Рассмотрим систему дифференциальных уравнений: В данной работе будем рассматривать систему, в случае когда ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
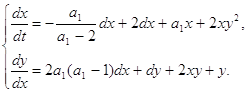
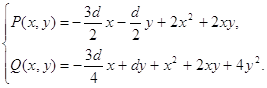






0 комментариев