Навигация
Исследование бесконечно-удаленной части плоскости
2.2 Исследование бесконечно-удаленной части плоскости
Очень важным для исследования вопроса о наличии замкнутых траекторий являются сведения о поведении траекторий при удалении в бесконечность, то есть исследование бесконечно-удаленных частей плоскости.
Для этого воспользуемся преобразованием Пуанкаре [7]:
![]() , (2.8)
, (2.8)
которое позволяет изучить особые точки лежащие на экваторе сферы Пуанкаре вне концов оси OY.
Имеем
![]()
![]()
Значит преобразование (2.8) переводит систему (1.1) в систему:
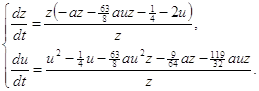 (2.9)
(2.9)
Введем новое время ![]() . Система (2.9) примет вид:
. Система (2.9) примет вид:
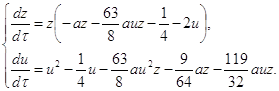 (2.10)
(2.10)
Изучим бесконечно-удаленные точки на оси u, т.е. при z=0.
Получаем
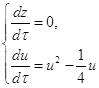 (2.11)
(2.11)
Приравнивая второе уравнение системы (2.11) к нулю, получаем
![]()
Таким образом, состоянием равновесия являются две точки N1(0,0) N2(0,![]() ).
).
Исследуем характер точек N1, N2.
1. Исследуем точку N1(0,0).
Составим характеристическое уравнение системы (2.10) в точке N1:
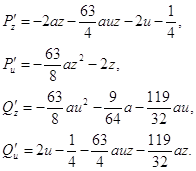 (2.12)
(2.12)
Согласно выражениям (2.12), получаем характеристическое уравнение:
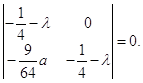
Получим, что
![]()
![]()
Корни ![]() - действительные и одного знака. Следовательно, точка N1(0,0) - устойчивый узел.
- действительные и одного знака. Следовательно, точка N1(0,0) - устойчивый узел.
2. Исследуем точку N2(0,![]() ).
).
Учитывая выражение (2.12), составим характеристическое уравнение в точке N2:
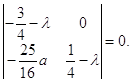
![]()
соответственно характеристическими числами будут являться
![]()
Корни ![]() - действительные и различных знаков. Следовательно, точка N2(0,
- действительные и различных знаков. Следовательно, точка N2(0,![]() )-седло.
)-седло.
Исследуем бесконечно-удаленную часть плоскости в конце оси OY с помощью преобразования [7]
![]()
Это преобразование систему (2.1) переводит в систему:
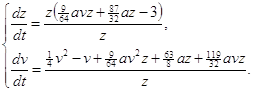 (2.14)
(2.14)
Введем новое время ![]() , тогда система (2.14) примет следующий вид:
, тогда система (2.14) примет следующий вид:
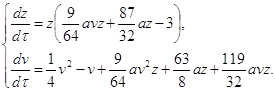 (2.15)
(2.15)
При z=0, получаем:
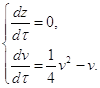 (2.16)
(2.16)
Приравнивая второе уравнение системы (2.16) к нулю, получаем
![]()
Для исследования состояний равновесий на концах оси OY, необходимо исследовать только точку N3(0,0).
Составим характеристическое уравнение системы (2.16) в точке N3:
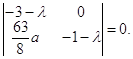
![]()
соответственно характеристическими числами будут являться
![]()
Корни ![]() - действительные и одного знака. Следовательно, точка N3(0,0) – устойчивый узел.
- действительные и одного знака. Следовательно, точка N3(0,0) – устойчивый узел.
Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 1.
Таблица 1.
| a | О | А | В | С | ∞ | ||
| N1 | N2 | N3 | |||||
| (-∞;0) | с | У+ | с | У- | У+ | с | У+ |
| (0;+∞) | с | У- | с | У+ | У+ | с | У+ |
Примечание: через с, у+, у- обозначены соответственно седло, устойчивый узел, неустойчивый узел.
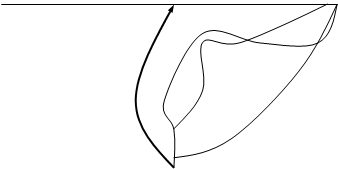
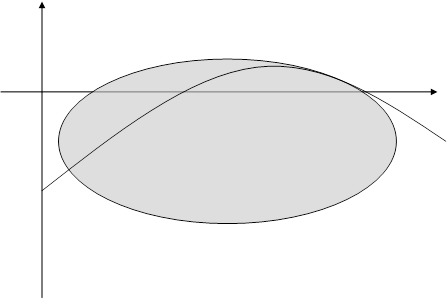
Положение кривых (1.4), (1.18) и расположение относительно их состояний равновесия при a>0 и a<0 дается соответственно рис. 1(а,б).
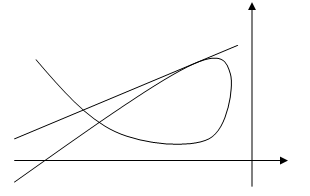
а) (a>0)
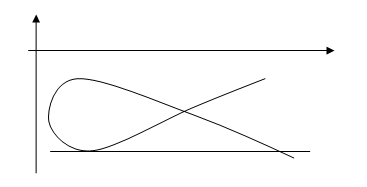
б) (a<0)
Рис.1
2.3 Построение качественной картины поведения траектории в круге Пуанкаре
Поскольку три состояния равновесия A, B, C расположены на интегральных кривых, то вопроса существования предельных циклов вокруг этих точек не возникает.
Начало координат расположено вне интегральных кривых и является седлом с индексом (-1). Предельные циклы могут окружать состояния равновесия с индексом (+1). Отсюда заключаем, что изучаемая система предельных циклов не имеет.
Поведение сепаратрис седла O, B легко выяснить.
Сепаратрисы седла В полностью определяются интегральными кривыми. Сепаратрисы седла О(0,0) однозначно выясняются с помощью изучения поля направления системы на осях координат. Так для а>0 α – сепаратрисы седла О примыкают к точке С и N3, а ω – сепаратрисы примыкают к точке А и N1, а при а<0 a-сепаратрисы примыкают к точке А и N1, w - сепаратрисы – к точке С и N3.
В результате получаем, что качественная картина исследования траекторий в целом при а>0 определяется рисунком 2а приложения, а при а<0 – рисунком 2б приложения.
ЗАКЛЮЧЕНИЕ
В данной дипломной работе построена квадратичная двумерная стационарная система, имеющая два частных интеграла в виде кривых третьего и первого порядков. При этом коэффициенты кривых выражаются через произвольный параметр системы.
Проведено качественное исследование полученной системы, найдены четыре состояния равновесия, три из которых А, В, С принадлежат интегральным кривым. Исследована бесконечно-удаленная часть плоскости, доказано отсутствия предельных циклов, выяснено поведение сепаратрис седел и построена качественная картина поведения траекторий системы в целом.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Баутин Н.Н. О числе предельных циклов, появляющихся при изменении коэффициентов из состояния равновесия типа фокуса или центра // Матем. сб.- 1952.- Т.30,№1.- 458 с.
2 Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости.-М.: Наука, 1976.- 274 с.
3 Бендиксон И. О кривых, определяемых дифференциальными уравнениями.- УМН, 1941.- Вып. 9.- 643 с.
4 Биркгоф Дж.Д. Динамические системы. М.-Л.: Гостехиздат, 1941.- 340 с.
5 Воробьев А.П. К вопросу о циклах вокруг особой точки типа “узел” // ДАН БССР.- 1960.- Т.4,№9.- 720 с.
6 Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую.- ПММ.- 1952.- Т.16, Вып. 6.- с.659-670.
7 Пуанкаре А. О кривых, определяемых дифференциальными уравнениями.- М.-Л.: ГИТТЛ, 1947.- 839 с.
8 Серебрякова Н.Н. Качественное исследование одной системы дифференциальных уравнений теории колебаний.- ПММ.- 1963 Т.27, Вып.1.- 230 с.
9 Филипцов В.Ф. К вопросу алгебраических интегралов одной системы дифференциальных уравнений // Дифференц. уравнения.- 1973.- Т.9,№3.- 256
10 Черкас Л.А. Об алгебраических решениях уравнения ![]() , где P и Q – многочлены второй степени // ДАН БССР.- 1963.- Т.7,№11.- 950 с.
, где P и Q – многочлены второй степени // ДАН БССР.- 1963.- Т.7,№11.- 950 с.
11 Яблонский А.И. Алгебраические интегралы одной системы дифференциальных уравнений // Дифференц. уравнения.- 1970.- Т.6,№10.- с. 1752-1760.
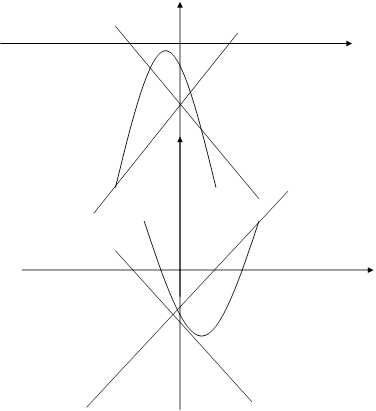
ПРИЛОЖЕНИЕ Поведение траекторий системы (2.1)
 |
 |
а) (а>0)
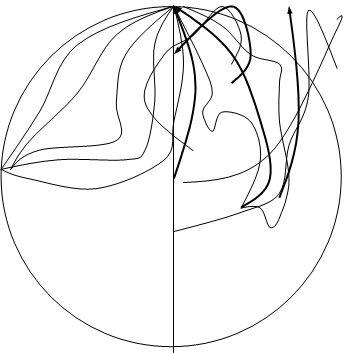 |
 |
б) (а<0)
Рис. 2
Похожие работы
... в целом выделенных в первом разделе классов систем при фиксированных значениях некоторых параметров. 1. Построение квадратичной двумерной стационарной системы 1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой второго порядка Рассмотрим систему дифференциальных уравнений: В данной работе будем рассматривать систему, в случае когда ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
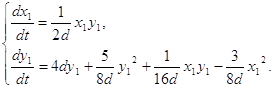
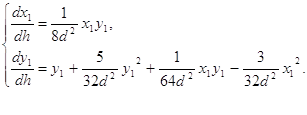
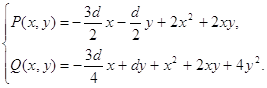






0 комментариев