Навигация
Нормированные пространства
1.2 Нормированные пространства
Определение: Множество ![]() называется нормированным пространством, если:
называется нормированным пространством, если:
1) ![]() – линейное пространство над полем действительных или комплексных чисел.
– линейное пространство над полем действительных или комплексных чисел.
2) Для каждого элемента ![]() определено вещественное число, называемое его нормой и обозначаемое
определено вещественное число, называемое его нормой и обозначаемое ![]() , и выполнены условия:
, и выполнены условия:
а) ![]() для любого
для любого ![]() ;
; ![]()
б) ![]() для любого
для любого ![]() и любого
и любого ![]() ;
;
в) ![]() , для любых
, для любых ![]()
([1], стр. 138).
Примеры нормированных пространств:
1. Пространство ![]() становится нормированным, если положить
становится нормированным, если положить ![]() .
.
2. Пространство ![]() с элементами
с элементами ![]() нормировано, при условии
нормировано, при условии 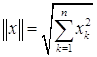 .
.
3. Пространство ![]() функций, непрерывных на отрезке
функций, непрерывных на отрезке ![]() , нормировано, если взять
, нормировано, если взять ![]() .
.
([1], стр. 139).
1.3 Банаховы пространства
Определение: Расстоянием (метрикой) между двумя элементами ![]() и
и ![]() называется вещественное неотрицательное число, обозначаемое
называется вещественное неотрицательное число, обозначаемое ![]() и подчиненное трем аксиомам:
и подчиненное трем аксиомам:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
Определение: Последовательность ![]() точек метрического пространства
точек метрического пространства ![]() называется фундаментальной, если
называется фундаментальной, если ![]() при
при ![]() .
.
Справедливы утверждения:
1. Если последовательность ![]() сходится к некоторому пределу, то она фундаментальна.
сходится к некоторому пределу, то она фундаментальна.
Доказательство:
Пусть ![]() , тогда
, тогда ![]() , при
, при ![]()
2. Всякая фундаментальная последовательность ![]() ограничена.
ограничена.
Определим расстояние в нормированном пространстве ![]() , полагая для любых
, полагая для любых ![]() . Тогда
. Тогда ![]() означает, что
означает, что ![]() . Это сходимость по норме.
. Это сходимость по норме.
Фундаментальная последовательность ![]() в нормированном пространстве в соответствии с определением расстояния характеризуется условием
в нормированном пространстве в соответствии с определением расстояния характеризуется условием
![]() , при
, при ![]()
Определение: Нормированное пространство называется полным, если всякая фундаментальная последовательность его элементов имеет предел.
Определение: Полное нормированное пространство называется банаховым пространством.
([2], стр. 137)
Похожие работы
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... : µ§. Шары такие : µ§ и µ§, причем: µ§ , µ§. µ§ µ§ Если µ§ ,то: µ§ , µ§ µ§ µ§ µ§ µ§ Теорема доказана. Единственность классического решения задачи Дирихле для уравнения Пуассона. µ§ µ§ (1) µ§ µ§ (2) µ§ - это не гарантирует существование решения. µ§ Теорема. Задача (1) (2) может иметь не более одного ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...


0 комментариев