Навигация
Оператор, сопряженный компактному оператору, компактен ([1], стр.241)
5. Оператор, сопряженный компактному оператору, компактен ([1], стр.241).
Примеры некомпактного и компактных операторов
Пусть ![]() – единичный оператор в банаховом пространстве
– единичный оператор в банаховом пространстве ![]() . Покажем, что если
. Покажем, что если ![]() бесконечномерно, то оператор
бесконечномерно, то оператор ![]() не вполне непрерывен. Для этого достаточно показать, что единичный шар в
не вполне непрерывен. Для этого достаточно показать, что единичный шар в ![]() (который переводится оператором
(который переводится оператором ![]() в себя) не компактен. Это в свою очередь вытекает из следующей леммы.
в себя) не компактен. Это в свою очередь вытекает из следующей леммы.
Лемма: Пусть ![]() – линейно независимые векторы в нормированном пространстве
– линейно независимые векторы в нормированном пространстве ![]() и пусть
и пусть ![]() – подпространство порожденное векторами
– подпространство порожденное векторами ![]() . Тогда существует последовательность векторов
. Тогда существует последовательность векторов ![]() , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) ![]()
2) ![]()
3) ![]()
![]() – расстояние вектора
– расстояние вектора ![]() от
от ![]() , т.е.
, т.е. 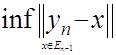
Пользуясь этой леммой, в единичном шаре всякого бесконечномерного нормированного пространства можно построить последовательность векторов ![]() , для которой
, для которой ![]() . Ясно, что такая последовательность не может содержать никакой сходящейся подпоследовательности. А это и означает отсутствие компактности.
. Ясно, что такая последовательность не может содержать никакой сходящейся подпоследовательности. А это и означает отсутствие компактности.
1.Простейшим примером компактного оператора является одномерный линейный оператор вида: ![]() , где
, где ![]() – фиксированный элемент из пространства
– фиксированный элемент из пространства ![]() , а
, а ![]() – фиксированный линейный функционал из пространства
– фиксированный линейный функционал из пространства ![]() , которое является банаховым пространством.
, которое является банаховым пространством.
2.Рассмотрим в пространстве ![]() оператор
оператор ![]() , преобразующий
, преобразующий ![]() в себя и задаваемый бесконечной системой равенств
в себя и задаваемый бесконечной системой равенств  при условии, что двойной ряд
при условии, что двойной ряд ![]() сходится. Такой оператор линеен и норма
сходится. Такой оператор линеен и норма 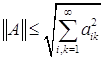 . Докажем что он компактен. Введем матричные линейные операторы
. Докажем что он компактен. Введем матричные линейные операторы ![]() в пространстве
в пространстве ![]() , определяемые матрицами
, определяемые матрицами ![]() , следующим образом:
, следующим образом:
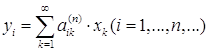 , где
, где ![]() при
при ![]() , и
, и ![]() при
при ![]() .
.
Иными словами, матрица ![]() получается из матрицы
получается из матрицы ![]() , если элементы всех строк
, если элементы всех строк ![]() , начиная с
, начиная с ![]() , заменить нулями. Отсюда вытекает, что, если
, заменить нулями. Отсюда вытекает, что, если ![]() , то, каков бы ни был элемент
, то, каков бы ни был элемент ![]() , будет
, будет ![]() при
при ![]() . Следовательно, совокупность значений каждого из операторов
. Следовательно, совокупность значений каждого из операторов ![]() конечномерна, а потому операторы
конечномерна, а потому операторы ![]() вполне непрерывны. Представим разность
вполне непрерывны. Представим разность ![]() с помощью матрицы. Из оценки
с помощью матрицы. Из оценки 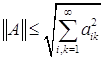 видно, что
видно, что  .
.
Следовательно, оператор ![]() компактен. ([2], стр. 307).
компактен. ([2], стр. 307).
3. В пространстве непрерывных функций ![]() важный класс компактных операторов образуют операторы вида:
важный класс компактных операторов образуют операторы вида:
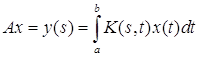 (3), где функция
(3), где функция ![]() непрерывна на квадрате
непрерывна на квадрате ![]() .
.
Покажем справедливость следующего утверждения: если функция ![]() непрерывна на квадрате
непрерывна на квадрате ![]() , то формула (3) определяет в пространстве
, то формула (3) определяет в пространстве ![]() компактный оператор.
компактный оператор.
Действительно, в указанных условиях интеграл (3) существует для любого ![]() из
из ![]() , то есть функция
, то есть функция ![]() определена. Пусть
определена. Пусть ![]() . На квадрате
. На квадрате ![]() функция
функция ![]() равномерно непрерывна по теореме Кантора, т.к. она непрерывна на замкнутом и ограниченном множестве в
равномерно непрерывна по теореме Кантора, т.к. она непрерывна на замкнутом и ограниченном множестве в ![]() . Значит,
. Значит,
![]()
![]()
![]()
![]() .
.
Оценим разность 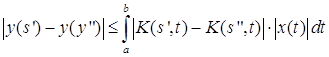 :
:
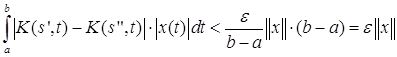 , при
, при ![]() .
.
Полученное равенство показывает, что функция ![]() непрерывна, то есть формула (3) действительно определяет оператор, переводящий пространство
непрерывна, то есть формула (3) действительно определяет оператор, переводящий пространство ![]() в себя.
в себя.
Из этого же неравенства видно, что если ![]() – ограниченное множество в
– ограниченное множество в ![]() , то соответствующее множество
, то соответствующее множество ![]() равностепенно непрерывно. Таким образом, если выполняется неравенство
равностепенно непрерывно. Таким образом, если выполняется неравенство ![]()
![]() , то
, то 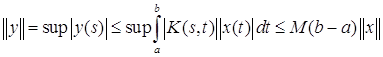 ,
,
То есть ограниченное множество перейдет в равномерно ограниченное. Таким образом, оператор (3) переводит всякое ограниченное множество из ![]() в множество функций, равномерно ограниченное и равностепенно непрерывное, т.е. предкомпактное по теореме Арцела.
в множество функций, равномерно ограниченное и равностепенно непрерывное, т.е. предкомпактное по теореме Арцела.
4. Оператор Вольтерра
Рассмотрим оператор  , где
, где 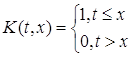 , в
, в ![]() .
.
Для доказательства компактности оператора Вольтерра покажем, что множество ![]() , равностепенно непрерывно и равномерно ограничено.
, равностепенно непрерывно и равномерно ограничено.
1) Равномерная ограниченность.
Оценим
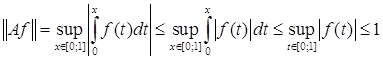 ,
,
а это значит, что множество равномерно ограниченно.
2) Равностепенная непрерывность.
По определению, равностепенная непрерывность означает, что
![]() . Возьмем произвольную функцию
. Возьмем произвольную функцию ![]() . Найдем ее образ
. Найдем ее образ  . Тогда
. Тогда 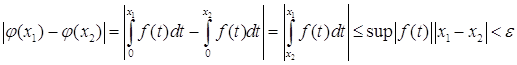 .
.
Тогда, если положить ![]() , равностепенная непрерывность показана.
, равностепенная непрерывность показана.
Таким образом, компактность оператора Вольтерра доказана.
Литература
1. Колмогоров, А.Н. Элементы теорий функций и функционального анализа [Текст] / А.Н. Колмогоров, С.В. Фомин. – М.: Физматлит, 2004.
2. Вулих, Б.З. Введение в функциональный анализ [Текст] / Б.З. Вулих. –Изд. 2, перераб. и доп. – М., 1967.
3. Князев, П.Н. Функциональный анализ [Текст] / П.Н. Князев– Изд. 2, перераб. М., 2003.
4. Люстерник, Л.А. Элементы функционального анализа [Текст] / Л.А. Люстерник В.И. Соболев– М., 1951.
Похожие работы
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... : µ§. Шары такие : µ§ и µ§, причем: µ§ , µ§. µ§ µ§ Если µ§ ,то: µ§ , µ§ µ§ µ§ µ§ µ§ Теорема доказана. Единственность классического решения задачи Дирихле для уравнения Пуассона. µ§ µ§ (1) µ§ µ§ (2) µ§ - это не гарантирует существование решения. µ§ Теорема. Задача (1) (2) может иметь не более одного ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...


0 комментариев