Линейные операторы и линейные функционалы

1.5 Линейные операторы и линейные функционалы

Пусть  – линейные нормированные пространства.

Определение: Линейным оператором, действующим из в , называется отображение , удовлетворяющее условию:  для любых , .

Будем говорить, что в  (вещественной или комплексной линейной системе) определен функционал , если каждому элементу  поставлено в соответствие некоторое вещественное (комплексное) число .

Определение: Линейный оператор, действующий из Е в Е₁, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное.

Определение: Оператор А называется непрерывным в точке , если для любой последовательности  выполняется условие .

Определение: Оператор А называется непрерывным, если он непрерывен в каждой точке пространства Е.

Теорема: Для того, чтобы линейный оператор  был непрерывным, необходимо и достаточно, чтобы он был ограничен.

Доказательство.

1. Пусть оператор А неограничен. Тогда существует МЕ – ограниченное множество, такое, что множество АМЕ₁ не ограничено. Следовательно, в Е₁ найдется такая окрестность нуля V, что ни одно из множеств АМ не содержится в V. Но тогда существует такая последовательность х_nM , что ни один из элементов Ах_n не принадлежит V и получаем, что  в Е, но  не сходится к 0 в Е; это противоречит непрерывности оператора А.

2. Если оператор А не непрерывен в точке 0, то в Е₁ существует такая последовательность , что Ах_n не стремится к 0. При этом последовательность  ограничена, а последовательность  не ограничена. Итак, если оператор А не непрерывен, то А и не ограничен.

Определение: Оператор называется конечномерным, если он ограничен и переводит данное пространство в конечномерное.

Определение: Функционал  называется линейным, если

Линейный функционал – это частный случай линейного оператора.

([1], стр. 217), ([1], стр. 125)

Примеры линейных функционалов:

1.         Пусть  – мерное арифметическое пространство с элементами  и  – произвольный набор из – фиксированных чисел. Тогда 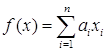 является линейным функционалом.

2.         Пример линейного функционала в

Пусть  – фиксированное целое положительное число. Для каждого  из  положим . Таким образом  является линейным функционалом в .

Похожие работы

Спектр оператора. Применение нестандартного анализа для исследования резольвенты и спектра оператора

Скачать

36187

0

5

... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при  существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...

Уравнения математической физики

Скачать

48279

5

0

... : µ§. Шары такие : µ§ и µ§, причем: µ§ , µ§. µ§ µ§ Если µ§ ,то: µ§ , µ§ µ§ µ§ µ§ µ§ Теорема доказана. Единственность классического решения задачи Дирихле для уравнения Пуассона. µ§ µ§ (1) µ§ µ§ (2) µ§ - это не гарантирует существование решения. µ§ Теорема. Задача (1) (2) может иметь не более одного ...

* Алгебры и их применение

Скачать

65703

0

0

... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...

*-Алгебры и их применение

Скачать

69018

1

0

... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...