Навигация
1.6. Сопряженные операторы
Определение: Совокупность всех непрерывных линейных функционалов, определенных на некотором линейном нормированном пространстве 
, образует линейное пространство, которое называется пространством, сопряженным с , и обозначается 
Рассмотрим непрерывный линейный оператор 
, отображающий линейное топологическое пространство в такое же пространство 
. Пусть 
– линейный функционал, определенный на , т. е. 
.
Применим функционал к элементу . Функционал 
есть непрерывный линейный функционал, определенный на . Обозначим его через 
. Функционал есть, таким образом, элемент пространства (сопряженное с ). Каждому функционалу мы поставили в соответствие функционал 
, т.е. получили некоторый оператор, отображающий 
в . Этот оператор называется сопряженным к оператору 
и обозначается 
. Обозначив значение функционала на элементе 
символом 
, получим, что 
, или 
.
Это соотношение можно принять за определение сопряженного оператора. ([1], стр. 229)
§2. Компактные операторы
2.1 Определение компактного оператора
Определение: Оператор , отображающий банахово пространство в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если он каждое ограниченное множество переводит в предкомпактное. ([1], стр.235).
Данное определение можно сформулировать в силу первого определения компактного множества следующим образом:
Определение: Пусть дан линейный оператор . Если он переводит любую ограниченную последовательность 
в 
, причем в можно выделить сходящуюся подпоследовательность, то такой оператор будем называть компактным.
2.2 Свойства компактных операторов
1. Из определения компактного оператора и ограниченности относительно компактного множества следует, что любой линейный компактной оператор является ограниченным, следовательно, непрерывным.
2. Если – компактный оператор, 
– ограниченный, то операторы 
и 
– компактные.
Доказательство. Если множество 
ограничено, то множество 
тоже ограничено. Следовательно, множество 
относительно компактно, а это и означает, что оператор вполне непрерывен. Далее, если 
ограничено, то 
относительно компактно, а тогда в силу непрерывности множество 
тоже относительно компактно, то есть оператор вполне непрерывен. Теорема доказана.
([1], стр.241).
3. Если операторы и компактные, действующие из нормированного пространства 
в нормированное пространство 
и 
– любые числа, то оператор 
также компактен.
Доказательство. Пусть множество 
ограничено. В его образе 
возьмем произвольную последовательность элементов 
. Тогда существуют 
, при которых 
. Положим 
. При этом 
. Так как множество 
компактно, а 
, то существует подпоследовательность 
, имеющая предел. Аналогично в компактном множестве 
из последовательности 
можно выделить подпоследовательность 
, имеющую предел. Но так как вместе с сходится и последовательность 
, то существует 
, что и доказывает компактность множества , а, следовательно, оператор 
компактен. ([2], стр.306).
4. Если 
– последовательность компактных операторов в банаховом пространстве , сходящаяся по норме к некоторому оператору , то оператор тоже компактен.
Доказательство. Для установления компактности оператора достаточно показать, что, какова бы ни была ограниченная последовательность 
элементов из , из последовательности 
можно выделить сходящуюся подпоследовательность.
Так как оператор 
компактен, то из последовательности. 
можно выбрать сходящуюся подпоследовательность. Пусть 
(2) – такая подпоследовательность, что 
сходится.
Рассмотрим теперь последовательность 
. Из неё тоже можно выбрать сходящуюся подпоследовательность. Пусть 
такая подпоследовательность выбранная из (2), что 
сходится. При этом, очевидно, что 
тоже сходится. Рассуждая аналогично, выберем из последовательности 
такую подпоследовательность 
, что 
сходится и т.д. Затем возьмем диагональную последовательность . Каждый из операторов 
переводит её в сходящуюся. Покажем, что и оператор тоже переводит её в сходящуюся. Тем самым мы покажем, что компактен. Так как пространство полно, то достаточно показать, что 
– фундаментальная последовательность. Имеем
.
Пусть 
, выберем сначала 
так, что 
, а потом выберем такое 
, чтобы при всех 
и 
выполнялось неравенство 
(это возможно, так как последовательность 
сходится). При этих условиях из предпоследнего неравенства получаем, что 
для всех достаточно больших 
и 
. Таким образом свойство доказано. ([1], стр. 239).
Похожие работы
Спектр оператора. Применение нестандартного анализа для исследования резольвенты и спектра оператора
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... : µ§. Шары такие : µ§ и µ§, причем: µ§ , µ§. µ§ µ§ Если µ§ ,то: µ§ , µ§ µ§ µ§ µ§ µ§ Теорема доказана. Единственность классического решения задачи Дирихле для уравнения Пуассона. µ§ µ§ (1) µ§ µ§ (2) µ§ - это не гарантирует существование решения. µ§ Теорема. Задача (1) (2) может иметь не более одного ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...
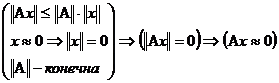
0 комментариев