Навигация
2. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность.
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.
2.1. Основные формулы
Средняя ошибка выборки при собственно случайном методе отбора (![]() ):
):
а) повторный отбор:
|
| (2.1) |
б) бесповторный отбор:
|
| (2.2) |
где n – численность выборочной совокупности;
N – численность генеральной совокупности;
s2 – дисперсия средней или доли;
![]() процент выборки.
процент выборки.
Дисперсия средней ![]() находится с использованием формул, указанных в п. 5.
находится с использованием формул, указанных в п. 5.
Дисперсия выборочной доли:
|
| (2.3) |
где ![]() - доля единиц, обладающих данным признаком в выборочной совокупности;
- доля единиц, обладающих данным признаком в выборочной совокупности;
m – единицы выборочной совокупности, обладающие данным признаком.
Предельная ошибка выборки ( D ):
|
| (2.4) |
где t – коэффициент кратности (доверия).
Доверительные интервалы:
| а) для средней: |
| (2.5) | ||
| б) для доли: |
| (2.6) | ||
Объем выборки при повторном отборе:
| а) для средней |
| (2.7) | |
| б) для доли: |
| (2.8) | |
Объем выборки при бесповторном отборе:
| а) для средней |
| (2.9) | ||
| б) для доли: |
| (2.10) | ||
2.2. Решение типовых задач
Задача № 2.1
В целях изучения затрат времени на изготовление детали рабочими завода проведена 10% случайная бесповторная выборка в результате которой получено данное распределение деталей по затратам времени, представлено в следующей таблице:
| Затраты времени на одну деталь, мин. | Число деталей, шт. | Расчетные значения | ||
| Середина интервала (X) |
|
| ||
| до 10 | 10 | 9 | 90 | 136,9 |
| до 12 | 20 | 11 | 220 | 57,8 |
| 12 – 14 | 50 | 13 | 650 | 4,5 |
| 14 – 16 | 15 | 15 | 225 | 79,35 |
| 16 и более | 5 | 17 | 85 | 92,45 |
| Итого | 100 | - | 1270 | 371 |
На основе этих данных вычислить:
1. С вероятностью 0.954 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе;
2. С вероятностью 0.954 предельную ошибку выборочной доли и границы удельного веса числа деталей с затратами времени на их изготовление от 10 до 14 мин.
Решение:
1. Определяем средние затраты времени на изготовление 1 детали для выборочной совокупности по формуле средней арифметической взвешенной:
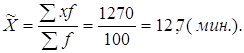
Рассчитываем дисперсию для выборочной совокупности по формуле средневзвешенной для сгруппированных данных:
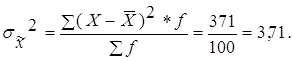
Так как выборка по условию задачи равна 10%, а n равно 100 шт., то N равно 1000 шт.Средняя ошибка выборки при бесповторном отборе рассчитывается по формуле:
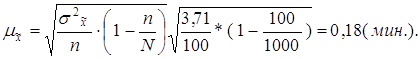
Так вероятность равна 0,954, то коэффициент доверия t равен 2. Предельная ошибка выборки определяется по формуле:
![]()
Доверительные интервалы (пределы) средней рассчитываем, исходя из двойного неравенства:
![]() ;
;
![]() ;
; ![]()
Таким образом, с вероятностью 0,954 можно утверждать, что средние затраты времени на изготовление одной детали на заводе лежат в границах от 12, 34 мин. до 13, 06 мин.
2. Определяем по выборочной совокупности долю деталей с затратами времени на их изготовление от 10 до 14 минут по формуле:
![]()
Тогда дисперсия выборочной доли равна:
![]()
Средняя ошибка выборки определяется по аналогичной формуле, что и для выборочной средней и равна:
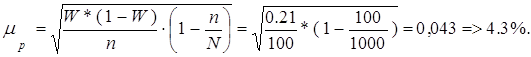
Предельная ошибка выборки для доли и доверительные интервалы определяется по формула:
![]()
![]()
![]()
![]() .
.
Таким образом, с вероятностью 0,954 можно утверждать, что доля деталей, изготовленных с затратами времени от 10 до 14 минут составляет от 61,3% до 78,9% в общем числе деталей.
Задача № 2.2
Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование методом случайного бесповторного отбора. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 3 года.
Определить количество студентов, которое нужно обследовать, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года.
Решение:
Так как обследование проведено методом бесповторного отбора для определения среднего возраста студентов, то необходимый объем выборки рассчитывается по формуле:
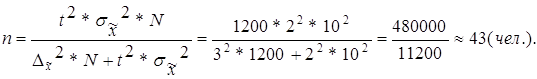
Таким образом, выборка численностью 43 человека обеспечивает заданную точность при бесповторном отборе.
2.3. Контрольные задачи
Задача № 2.1
В целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом (бесповторном) способе отбора 5% изделий получены определенные данные о весе обследованных единиц, представленные в следующей таблице:
| Вес изделий, г. | Число образцов, шт. |
| до 100 | 22 |
| 100– 110 | 76 |
| 110 – 120 | 215 |
| 120 – 130 | 69 |
| 130 и свыше | 18 |
| Итого | 400 |
На основании выборочных данных вычислить:
1. По «способу моментов»:
а) средний вес изделия;
б) дисперсию.
2. Cреднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0.997 возможные границы, в которых заключен средний вес изделий во всей партии.
5. С вероятностью 0.954 возможные границы удельного веса (доли) стандартной продукции во всей партии при условии, что к стандартной продукции относятся все изделия с весом от 100 г до 130 г.
Задача № 2.2
Для изучения возрастной структуры рабочих завода по состоянию на 1 июля было проведено 3% выборочное обследование по методу случайного бесповторного отбора. Результаты обследования распределения рабочих по возрасту представлены в следующей таблице:
| Группы рабочих по возрасту, лет. | Число рабочих, чел. |
| до 20 | 10 |
| 20 – 30 | 18 |
| 30 – 40 | 40 |
| 40 –50 | 24 |
| 50 и старше | 8 |
| Итого | 100 |
На основании данных выборочного обследования вычислите:
1. По «способу моментов»:
а) средний возраст рабочего;
б) дисперсию.
2. Среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0.997 возможные границы среднего возраста рабочих завода.
5. С вероятностью 0.954 возможные границы доли рабочих завода, возраст которых составляет менее 20 лет.
Задача № 2.3
При изучении производительности труда работников торговли произведено 10% -ое выборочное обследование выполнения норм выработки кассирами магазинов. В результате механического отбора получены следующие данные о распределении выборочной совокупности по выполнению норм выработки, представленные в таблице:
| Выполнение норм выработки, % | Число кассиров, чел. |
| до 90 | 3 |
| 90 – 100 | 7 |
| 100 – 110 | 30 |
| 110 – 120 | 25 |
| 120 – 130 | 17 |
| 130 – 140 | 9 |
| 140 – 150 | 6 |
| 150 и выше | 3 |
| Итого | 100 |
По данным выборки определить для генеральной совокупности:
1. С вероятностью 0.954 пределы значения доли кассиров, выполняющих норму выработки.
2. С вероятностью 0.997 пределы, в которых находится средний процент выполнения кассирами норм выработки.
Задача № 2.4
На электроламповом заводе в порядке 5% механической выборки проверено 2000 лампочек, из которых 20 забраковано. Определить с вероятностью 0,997, в каких пределах колеблется процент бракованных лампочек.
Задача № 2.5
В порядке механической 5%-ой выборки было подвергнуто испытанию на разрыв 1000 нитей из партии. Установлено, что средняя крепость пряжи равняется 340 г при среднем квадратическом отклонении 20 г. С вероятностью 0,954 определите пределы, в которых находится средняя крепость пряжи в партии.
Задача № 2.6
В городе Н с числом семей 15000 предполагается методом случайного бесповторного отбора определить долю семей с детьми ясельного возраста. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,03, если на основе предыдущих обследований известно, что дисперсия равна 0,3.
2.4. Контрольные вопросы
1. Преимущества выборочного наблюдения перед сплошным.
2. Дать определение понятий: ошибка наблюдения, ошибка регистрации, ошибка репрезентативности, максимально возможная ошибка.
3. Условия правильного отбора единиц совокупности при выборочном наблюдении.
4. Генеральная и выборочная совокупности.
5. Различия между повторной и бесповторной выборками.
6. Формулы взаимосвязи средней и предельной ошибки выборки.
7. Формулы расчета средней ошибки при повторном и бесповторном отборе.
8. Неравенства, устанавливающие возможные пределы, в которых будут находиться характеристики генеральной совокупности.
9. Формулы для расчета необходимого объема выборки.
10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова.
11. Распространение результатов выборочного наблюдения на генеральную совокупность.
2.5. Тесты
1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется:
а) выборочной;
б) генеральной;
в) однородной;
г) свой ответ.
2. Виды ошибок статистических наблюдений:
а) регистрации;
б) систематические;
в) случайные;
г) репрезентативности;
д) все ответы верны.
3. По методу отбора различают:
а) бесповторный отбор;
б) случайный отбор;
в) повторный отбор;
г) все ответы верны.
4. Если количество единиц в совокупности меньше 30, то выборка считается:
а) большой;
б) малой;
в) средней;
г) нет верного ответа.
5. Виды выборок:
а) случайная;
б) типическая;
в) механическая;
г) групповая.
6. При 6%-ой выборке из партии деталей в 600 ед. объем выборки n составляет:
а) 54 ед;
б) 36 ед;
в) 46 ед.
7. Для характеристики надежности выборочных показателей различают следующие виды ошибок выборки:
а) среднюю;
б) случайную;
в) предельную;
г) репрезентативности.
8. Размер средней ошибки выборки зависит от:
а) объема выборки;
б) однородности совокупности;
в) ассиметрии;
г) степени варьирования изучаемого признака.
9. Чем больше численность выборки при прочих равных условиях, тем величина средней ошибки выборки:
а) больше;
б) меньше;
в) точнее
г) свой ответ.
10. Чем больше вариация признака, тем ______ средняя ошибка выборки:
а) больше;
б) меньше;
в) точнее;
г) свой ответ.
11. Средняя ошибка выборки показывает __________.
12. Средняя ошибка выборки имеет единицы измерения:
а) что и количественный признак;
б) не имеет единиц измерения;
в) представлена коэффициентом;
г) в процентах.
13. Для отбора единиц из неоднородной совокупности применяется:
а) типическая выборка;
б) механическая выборка;
в) собственно-случайная выборка;
г) серийная выборка.
14. Отбор единиц из генеральной совокупности посредством жеребьевки или какого-либо иного подобного способа – это:
а) типическая выборка;
б) механическая выборка;
в) собственно-случайная выборка;
г) серийная выборка.
15. Доверительные интервалы (пределы) для средней ___________.
16. Для скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 22 дня со стандартным отклонением 6 дней.
Определить с вероятностью p равной 0,954 предельную ошибку выборочной средней и доверительные пределы средней продолжительности расчетов предприятий данной корпорации.
а) 1,2 дня; ![]() ;
;
б) 2,2 дня; ![]() ;
;
в) 3 дня; ![]() .
.
Похожие работы
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... обзоры (опросы общественного мнения). Обзоры состоят из 4 элементов: 1. выборочного наблюдения 2. анкетирование 3. интервью 4. анализы результата При выборочном наблюдении исследования рекламной деятельности существуют 3 вида отбора представителей общества для опроса: - одноступенчатый отбор (простой выбор человека из всей совокупности людей); - серийный отбор (в качестве единиц опроса ...
... . Коэффициент асимметрии показывает, что существует значительная асимметрия. Отрицательный показатель эксцесса показывает, что разброс показателя достаточно велик. Цель вариационного анализа достигнута. 3. Выборочное наблюдение Произведем отбор 27 и 35 субъектов из генеральной совокупности. Будем производить случайный отбор субъектов РФ. Составим две таблицы из 27 и 35 субъектов ...
... 0,997 С вероятностью 0,997 можно утверждать, что средний разряд рабочих механического цеха находится в пределах , . 4 Определение необходимой численности выборки В практике проведения выборочного наблюдения возникает потребность в определении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли. Формально вопрос ...
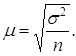
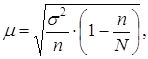
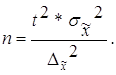
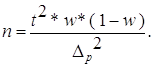
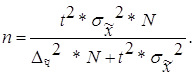
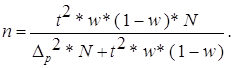
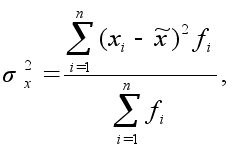
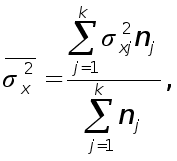
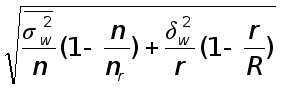
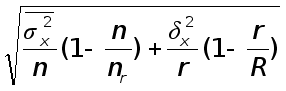

0 комментариев