Навигация
Среди выборочного обследования 1000 семей региона по уровню душевого дохода (выборка 2%-ая, механическая) малообеспеченных оказалось 300 семей
17. Среди выборочного обследования 1000 семей региона по уровню душевого дохода (выборка 2%-ая, механическая) малообеспеченных оказалось 300 семей.
Определить с вероятностью 0,997 долю малообеспеченных семей во всем регионе и доверительные интервалы.
а) 2%; ![]() ;
;
б) 1,4%; ![]() ;
;
в) 5%; ![]() .
.
18. Для определения доли рабочих со стажем работы 20 лет и более на заводе с числом рабочих 10000 была проведена механическая выборка. Определить какова должна быть численность, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,05, если на основе предыдущих обследований известно, что дисперсия равна 0,2.
а) 300 чел.;
б) 500 чел.;
в) 250 чел..
3. РЯДЫ ДИНАМИКИ
Ряд динамика представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени. Построение и анализ рядов динамики позволяет выявить и измерить закономерности развития общественных явлений во времени.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней ряда: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
3.1. Основные формулы
Таблица 3.1 – Основные характеристики ряда динамики
| Показатель | Цепной | Базисный |
| Абсолютный прирост |
где |
где |
| Взаимосвязь: | ||
| Темп роста |
|
|
| Взаимосвязь: | ||
| Темп пророста |
|
|
|
| ||
| Абсолютное значение одного процента |
| |
Таблица 3.2 – Средние показатели ряда динамики
| Показатель | Цепной | Базисный |
| Средний абсолютный прирост |
где n – число цепных абсолютных приростов в изучаемом периоде. |
где m – число уровней ряда динамики в изучаемом периоде, включая базисный. |
| Средний темп роста |
где n – число цепных коэффициентов роста; |
|
| Темп прироста |
| |
Таблица 3.3 – Средний уровень ряда
| Ряд динамики | Формула среднего уровня ряда |
| Для интервальных рядов динамики из абсолютных уровней | |
| - при равных интервалах |
где y – абсолютные уровни ряда; n – число уровней ряда. |
| - при неравных интервалах |
где t – веса, длительность интервалов времени между смежными датами. |
| Для моментных рядов динамики | |
| - с равностоящими уровнями |
|
| - с неравностоящими уровнями |
|
Таблица 3.4 – Измерение связи. Уравнения регрессии
| Линейная |
где t- время. |
| Гиперболическая |
|
| Параболическая |
|
| Экспоненциальная |
|
| Степенная |
|
| Логарифмическая |
|
| Показательная |
|
Параметры а0 и а1 определяются из системы уравнений:
а) линейная регрессия:
|
| |
|
| (3.1) |
б) парабола второго порядка:
|
| |
|
| |
|
| (3.2) |
в) гипербола:
|
| |
|
| (3.3) |
Для определения границ интервалов прогнозируемых явлений:
|
| (3.4) |
где ![]() – коэффициент доверия по распределению Стьюдента;
– коэффициент доверия по распределению Стьюдента;
![]() – остаточное среднее квадратическое отклонение от тренда:
– остаточное среднее квадратическое отклонение от тренда:
|
| (3.5) |
где m – число параметров адекватной модели тренда;
n – число уровней ряда динамики.
3.2. Решение типовых задач
Задача № 3.1
Динамика производства электроэнергии в Украине характеризуется следующими данными, представленными в таблице 3.5 (столбец 1– 2):
Рассчитать:
1. Цепные и базисные аналитические показатели ряда динамики.
Проверить взаимосвязи.
2. Средние: уровень ряда, абсолютный прирост, темпы роста и прироста.
Таблица 3.5 – Исходные данные и расчетные значения
| Год | Производство электроэнергии, млрд. кВт*ч | Расчетные значения | |||
| Абсолютный прирост, млрд. кВт*ч | Темп роста, % | ||||
|
|
|
|
| ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2001 | 957 | – | – | – | 100 |
| 2002 | 876 | 876-957=-81 | 876-957=-81 |
|
|
| 2003 | 860 | 860-876=-16 | 860-957=-97 |
|
|
| 2004 | 847 | 847-860=-13 | 847-957=-110 |
|
|
| 2005 | 834 | -13 | -123 | 98,5 | 87,1 |
| 2006 | 827 | -7 | -130 | 99,2 | 86,4 |
Продолжение таблицы 3.5
| Год | Расчетные значения | ||
| Темп прироста, % | Абсолютное значение одного процента прироста, млрд. КВт*ч | ||
|
|
|
| |
| 1 | 2 | 3 | 4 |
| 2001 | – | – | – |
| 2002 | 91,5-100 = -8,5 | 91,5-100 = -8,5 |
|
| 2003 | 98,2-100 = -1,8 | 89,7-100 = -10,3 |
|
| 2004 | 98,5-100 = -1,5 | 88,5-100 = -11,5 |
|
| 2005 | -1,5 | -12,9 | 8,47 |
| 2006 | -0,8 | -13,6 | 8,34 |
Решение:
1. Проверка взаимосвязей:
а) абсолютных приростов:
![]()
б) темпов роста:
![]()
2. Так как исследуемый ряд динамики представляет собой интервальный ряд с одинаковыми интервалами, то расчет среднего размера производства электроэнергии производим по формуле:
![]()
Средний абсолютный прирост рассчитывается по формулам:
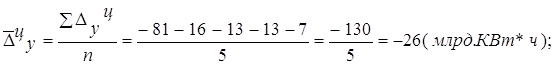
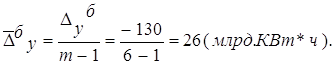
Cредний темп роста определяем по формулам:
![]()
![]()
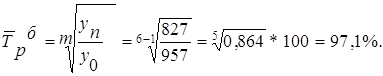
Средний темп прироста определяется по формуле:
![]()
![]()
Задача № 3.2
Имеются данные об урожайности зерновых культур (исходные данные в столбцах 1 и 2):
| Месяц | Фактическая урожайность, ц. (y) | Расчетные значения | |||||
| t |
|
|
|
|
| ||
| Январь | 15,4 | -9 | 81 | -138,6 | 15,15 | 0,25 | 0,0625 |
| Февраль | 14,0 | -7 | 49 | -98,0 | 15,19 | -1,19 | 1,4161 |
| Март | 17,6 | -5 | 25 | -88,0 | 15,23 | 2,37 | 5,6169 |
| Апрель | 15,4 | -3 | 9 | -46,2 | 15,28 | 0,12 | 0,0144 |
| Май | 10,9 | -1 | 1 | -10,9 | 15,32 | -4,42 | 19,5364 |
| Июнь | 17,5 | 1 | 1 | 17,5 | 15,36 | 2,14 | 4,5796 |
| Июль | 15,0 | 3 | 9 | 45,0 | 15,4 | -0,40 | 0,016 |
| Август | 18,5 | 5 | 25 | 92,5 | 15,45 | 3,05 | 9,3025 |
| Сентябрь | 14,2 | 7 | 49 | 99,4 | 15,49 | -1,29 | 1,6641 |
| Октябрь | 14,9 | 9 | 81 | 134,1 | 15,53 | -0,63 | 0,3969 |
| Итого | 153,4 | 0 | 330 | 6,8 | 153,4 |
| 42,6054 |
Определить урожайность на ноябрь текущего года, построив линейную трендовую модель.
Решение:
Для выравнивания ряда используем линейную трендовую модель –
уравнение прямой: ![]()
Параметры искомого уравнения прямой определяем из следующей системы нормальных уравнений:
![]()
![]() откуда
откуда ![]()
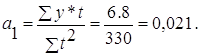
Уравнение прямой будет иметь вид: ![]()
Подставляя в данной уравнение последовательно значения t, равные -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, находим выровненные уровни ![]() .
.
Если ![]() , в нашем примере эти суммы равны между собой и равны 153,4, следовательно, значения уровней выровненного ряда найдены верно.
, в нашем примере эти суммы равны между собой и равны 153,4, следовательно, значения уровней выровненного ряда найдены верно.
Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности зерновых культур в среднем на ![]() в месяц.
в месяц.
Используя полученное уравнение методом экстраполяции при t равном 11, определяем ожидаемую урожайность культур на ноябрь текущего года:
![]()
Зная точечную оценку прогнозируемого значения урожайности ![]() , определяем вероятностные границы интервала по формуле:
, определяем вероятностные границы интервала по формуле:
![]()
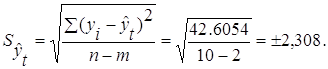
При доверительной вероятности, равной 0,95, коэффициент доверия Стьюдента равен 2,306.
![]()
![]()
Таким образом, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в ноябре текущего года будет не менее чем 10,25, но и не более чем 20,89 ц/га.
Похожие работы
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... обзоры (опросы общественного мнения). Обзоры состоят из 4 элементов: 1. выборочного наблюдения 2. анкетирование 3. интервью 4. анализы результата При выборочном наблюдении исследования рекламной деятельности существуют 3 вида отбора представителей общества для опроса: - одноступенчатый отбор (простой выбор человека из всей совокупности людей); - серийный отбор (в качестве единиц опроса ...
... . Коэффициент асимметрии показывает, что существует значительная асимметрия. Отрицательный показатель эксцесса показывает, что разброс показателя достаточно велик. Цель вариационного анализа достигнута. 3. Выборочное наблюдение Произведем отбор 27 и 35 субъектов из генеральной совокупности. Будем производить случайный отбор субъектов РФ. Составим две таблицы из 27 и 35 субъектов ...
... 0,997 С вероятностью 0,997 можно утверждать, что средний разряд рабочих механического цеха находится в пределах , . 4 Определение необходимой численности выборки В практике проведения выборочного наблюдения возникает потребность в определении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли. Формально вопрос ...
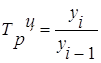
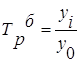
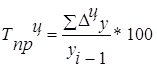
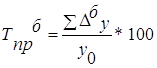 *100
*100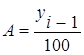
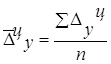 ,
,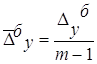 ,
,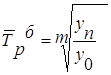
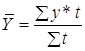 ,
,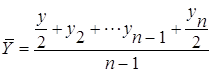
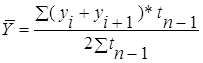
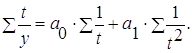
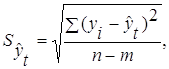
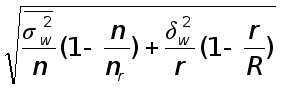
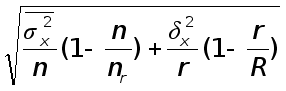

0 комментариев