Навигация
Сеточные методы для нестационарных задач
7. Сеточные методы для нестационарных задач
Уменьшение величины шага приводит к квадратичному возрастанию числа точек в области решения, а следовательно, к порядку алгебраической системы уравнений. Одним из путей уменьшения числа уравнений является метод прямых, который позволяет аппроксимировать дифференциальное уравнение в частных производных системой дифференциальных уравнений в обыкновенных производных с краевыми условиями. Для этого частные производные по одной из независимых переменных не заменяют конечно-разностным эквивалентом. Если в уравнении оставлена пространственная переменная, то получаемая система будет краевой задачей со всеми сложностями ее решения, рассмотренными ранее.
Существенным будет выигрыш лишь при решении дифференциальных уравнений в частных производных, описывающих нестационарные процессы. К ним относятся уравнения, подобные уравнениям теплопроводности и волновому. Этим уравнениям кроме условий на границе задают еще и начальное распределение искомой функции во всех точках области решения.
Применение метода прямых рассмотрим на примере решения уравнения теплопроводности следующего вида:
![]() ,
,
которое описывает распространение тепла (изменение температуры) вдоль металлического стержня, вваренного своими концами в две металлические пластины с разными, постоянно поддерживаемыми на них температурами. Коэффициент B, характеризующий свойства материала, возьмем равным 1.
Пусть расстояние между пластинами равно единице, т.е. ![]() , значения температуры на пластинах
, значения температуры на пластинах ![]() и начальное распределение температуры по длине
и начальное распределение температуры по длине ![]() .
.
Разобьем единичную длину стержня на 8 равных частей (h=1/8) и обозначим значение температуры в каждой точке через ![]() , k=0,1,..., Применим пяти- и шести точечную аппроксимацию частной производной второго порядка: первую симметричную - для внутренних точек, и вторую (несимметричную) – для приграничных точек
, k=0,1,..., Применим пяти- и шести точечную аппроксимацию частной производной второго порядка: первую симметричную - для внутренних точек, и вторую (несимметричную) – для приграничных точек ![]() . Температуры в точках с k=0 и k=8 заданы: 100° и 0°.
. Температуры в точках с k=0 и k=8 заданы: 100° и 0°.
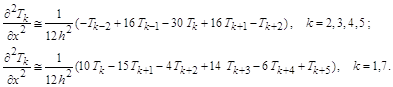
После замены производных конечно-разностными эквивалентами получим следующую систему линейных дифференциальных уравнений с начальными условиями ![]() в векторно-матричной форме:
в векторно-матричной форме:
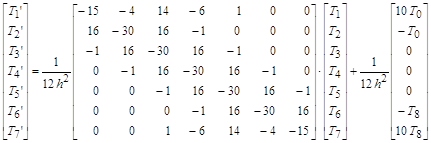
Чтобы получить представление о влиянии порядка разностных формул на вид записи и точность решения задачи, в таблице приведены системы уравнений для 5- и 3-точечных выражений частных производных:
| Произ-водная |
|
|
|
| T1’= | -15T1-4T2+14T3-6T4+T5+1000 | -20T1+6T2+4T3-T4+1100 | -2T1+T2+100 |
| T2’= | 16T1-30T2+16T3-T4-100 | 16T1-30T2+16T3-T4-100 | T1-2T2+T3 |
| T3’= | -T1+16T2-30T3+16T4-T5 | -T1+16T2-30T3+16T4-T5 | T2-2T3+T4 |
| T4’= | -T2+16T3-30T4+16T5-T6 | -T2+16T3-30T4+16T5-T6 | T3-2T4+T5 |
| T5’= | -T3+16T4-30T5+16T6-T7 | -T3+16T4-30T5+16T6-T7 | T4-2T5+T6 |
| T6’= | -T4+16T5-30T6+16T7 | -T4+16T5-30T6+16T7 | T5-2T6+T7 |
| T7’= | T3-6T4+14T5-4T6-15T7 | -T4+4T5+6T6-20T7 | T6-2T7 |
Полученные системы обыкновенных дифференциальных уравнений можно решать любым из рассмотренных ранее численным методом. Правда, появляется особенность в выборе шага интегрирования по времени, который теперь зависит еще и от шага разбиения области решения по пространственной переменной. В случае аппроксимации производной по времени конечными разностями “вперед” соотношение между шагом по временной переменной ![]() и по пространственной
и по пространственной ![]() должно подчиняться следующему неравенству:
должно подчиняться следующему неравенству: ![]() . При несоблюдении неравенства решение будет численно неустойчивым и интегрирование по времени с каждым шагом будет давать неограниченно возрастающие значения.
. При несоблюдении неравенства решение будет численно неустойчивым и интегрирование по времени с каждым шагом будет давать неограниченно возрастающие значения.
В рассматриваемом примере ![]() =
=![]() 0,015625, поэтому интегрирование трех систем по формулам Рунге-Кутта было выполнено с шагом по времени
0,015625, поэтому интегрирование трех систем по формулам Рунге-Кутта было выполнено с шагом по времени ![]() = 0,001 до значения 0,01 и с шагом 0,005 – до значения времени, равного 0,75. Выборка ряда значений температуры из решений в интервале времени (0,0.75] показана в таблице колонками из трех чисел, соответствующих сверху-вниз трем приведенным выше системам.
= 0,001 до значения 0,01 и с шагом 0,005 – до значения времени, равного 0,75. Выборка ряда значений температуры из решений в интервале времени (0,0.75] показана в таблице колонками из трех чисел, соответствующих сверху-вниз трем приведенным выше системам.
|
|
|
|
|
|
|
|
|
| 0.01 | 36.32 36.82 23.97 | 152 466 3.434 | 0.9573 1.038 0.3456 | -0.005579 0.004583 0.02668 | -0.02021 -0.02009 0.001666 | -0.001651 -0.002840 73610^(-5) | 0.009336 -0.0001931 3.93410^(-6) |
| 0.02 | 52.52 52.39 37.89 | 20.86 21.00 9.682 | 6.165 6.287 1.825 | 1.298 1.347 0.2702 | 0.1715 0.1810 0.0328 | 0.01656 0.002515 0.003367 | 0.03366 -0.01559 0.0002973 |
| 0.05 | 69.3 69.17 57.27 | 42.88 42.79 26.61 | 23.52 23.50 10.15 | 11.37 11.37 3.243 | 4.821 4.826 0.884 | 1.773 1.767 0.2089 | 0.5202 0.5142 0.04223 |
| 0.1 | 77.99 77.98 69.09 | 57.61 57.58 42.81 | 40.14 40.12 23.71 | 26.27 26.25 11.75 | 16 15.99 5.222 | 826 829 2.076 | 3.842 3.854 0.6867 |
| 0.25 | 85.43 85.43 80.18 | 71.18 71.18 61.57 | 57.51 57.51 45.12 | 44.6 44.60 31.4 | 32.51 32.51 20.52 | 21.18 21.18 12.13 | 10.43 10.43 5.581 |
| 0.5 | 87.32 87.32 85.39 | 74.67 74.67 71.1 | 62.07 62.07 57.41 | 49.54 49.54 44.5 | 37.07 37.07 32.42 | 24.67 24.67 21.11 | 12.32 12.32 10.39 |
| 0.75 | 87.48 87.48 86.87 | 74.97 74.97 73.84 | 62.46 62.46 60.99 | 49.96 49.96 437 | 37.46 37.46 35.99 | 24.97 24.97 23.84 | 12.48 12.48 11.87 |
Как видно, трех точечная аппроксимация по сравнению с пятиточечной дает худший результат. Точное решение в установившемся режиме дает изменение температуры на каждой одной восьмой длины стержня 12,5°С. Пятиточечная аппроксимация в данной задаче дала погрешность в сотые доли процента.
Литература
1. Калашников В. И. Введение в численные методы: Учеб. пособие. – Харьков: НТУ “ХПИ”, 2002. – 132 с.
2. Рено Н.Н. АЛГОРИТМЫ ЧИСЛЕННЫХ МЕТОДОВ: МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВУЗОВ. Изд-во: "Книжный дом Университет" (КДУ), 2007. – 24с.
3. Самарcкий А. А. Задачи и упражнения по численным методам. Изд.3 Изд-во: КомКнига, ЛКИ, 2006. – 208с.
4. Самарский А.А. Введение в численные методы Учебное пособие для вузов 3-е изд.,стер. ЛАНЬ, 2005. – 288с.
5. Турчак Л. И., Плотников П. В. Основы численных методов. Изд-во: ФИЗМАТЛИТ®, 2003. – 304с.
6. Тыртышников Е.Е. МЕТОДЫ ЧИСЛЕННОГО АНАЛИЗА (1-Е ИЗД.) УЧЕБ. ПОСОБИЕ Издательство "Академия/Academia", 2007. – 320с.
Похожие работы
... схема со сглаживанием, схема прямоугольник со сглаживанием, “шахматная ” схема. Произведены некоторые расчеты для одномерного уравнения переноса с переменными и постоянными коэффициентами на неравномерных сетках, с целью определения наиболее устойчивой разностной схемы. Исследование показало, что наиболее устойчивым методом для одномерного уравнения переноса с переменными коэффициентами является ...
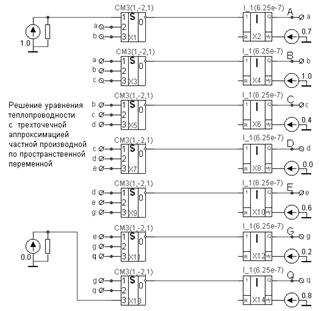
... . Результаты моделирования можно просматривать на экране монитора и распечатывать на принтере. В данном расчетно-графическом задании виртуальная гибридная вычислительная машина будет использована в качестве вычислительного инструмента для решения краевых задач методами математического и аналогового моделирования, с целью демонстрации возможностей аналоговых устройств для исследования физических ...
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... суммы и позволит вычислить приближенное значение приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно ...




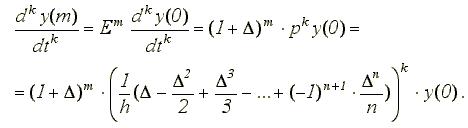


0 комментариев