Навигация
Разностные схемы для уравнений в частных производных
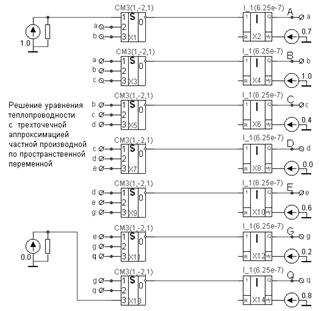
5. Разностные схемы для уравнений в частных производных
Конечно-разностная аппроксимация дифференциальных уравнений в частных производных, называемая в литературе методом сеток, использует те же конечно-разностные выражения производных через значения искомой функции, которые приведены в таблицах выше. Однако есть особенности, которые связаны с наличием у каждой рассматриваемой точки соседних точек не только по направлениям осей независимых переменных, но и во множестве других наклонных направлений.
Поэтому, в случае использования многоточечных (более трех точек) формул для производных, выражения последних могут разрабатываться дополнительно для каждого применения.
Наиболее удобным в разработке многоточечных конечно-разностных выражений для уравнений в частных производных является операторный метод, основанный на учете взаимосвязи оператора дифференцирования с операторами сдвига по направлениям различных независимых переменных. Рассмотрим его применение на примере построения разностных формул для двумерных уравнений в частных производных второго порядка.
Характерным представителем уравнений в частных производных второго порядка является уравнение Лапласа:
![]()
![]() ,
,
где ![]() – непрерывная функция, заданная на границе области.
– непрерывная функция, заданная на границе области.
Область численного решения уравнения разобьем на клетки системой вертикальных и горизонтальных прямых, проходящих через равномерно расположенные с шагом h точки на осях координат соответственно x и y:
![]()
Значения функции в узлах сетки обозначим через ![]() и для каждой точки области решений частные производные из уравнения заменим соответствующим (например, трех точечным) симметричным конечно-разностным выражением для внутренних точек и для точек вблизи границ таким несимметричным, чтобы значения функций не выходили за пределы области:
и для каждой точки области решений частные производные из уравнения заменим соответствующим (например, трех точечным) симметричным конечно-разностным выражением для внутренних точек и для точек вблизи границ таким несимметричным, чтобы значения функций не выходили за пределы области:
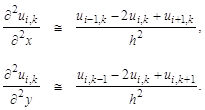
После подстановки в уравнение Лапласа этих выражений для каждой внутренней точки области будет получена система алгебраических уравнений следующего вида:
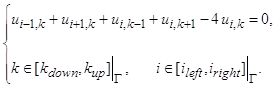
В качестве примера, демонстрирующего применение метода сеток, приведем решение уравнения Лапласа для прямоугольной области с количеством узлов ![]() и значениями функции на границе, как показано ниже:
и значениями функции на границе, как показано ниже:
| u(0,0) | 0.5 | 0.476 | 0.404 | 0.294 | 0.154 | 0 |
| 0.5 | u(1,1) | u(1,2) | u(1,3) | u(1,4) | u(1,5) | 0 |
| 0.476 | u(2,1) | u(2,2) | u(2,3) | u(2,4) | u(2,5) | 0 |
| 0.404 | u(3,1) | u(3,2) | u(3,3) | u(3,4) | u(3,5) | 0 |
| 0.294 | u(4,1) | u(4,2) | u(4,3) | u(4,4) | u(4,5) | 0 |
| 0.154 | u(5,1) | u(5,2) | u(5,3) | u(5,4) | u(5,5) | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Уравнения для 25 внутренних точек u(i,k):
| 0.5-4·u(1,1)+u(1,2)+u(2,1) +0.5=0, u(1,1)-4·u(2,1)+u(2,2)+u(3,1)+0.476=0, u(2,1)-4·u(3,1)+u(3,2)+u(4,1)+0.404=0, u(3,1)-4·u(4,1)+u(4,2)+u(5,1)+0.294=0, u(4,1)-4·u(5,1)+u(5,2)+0.154=0, 0.476+u(1,1)-4·u(1,2)+u(1,3)+u(2,2)=0, u(1,2)+u(2,1)-4·u(2,2)+u(2,3)+u(3,2)=0, u(2,2)+u(3,1)-4·u(3,2)+u(3,3)+u(4,2)=0, u(3,2)+u(4,1)-4·u(4,2)+u(4,3)+u(5,2)=0, u(4,2)+u(5,1)-4·u(5,2)+u(5,3)=0, 0.404+u(1,2)-4·u(1,3)+u(1,4)+u(2,3) =0, u(1,3)+u(2,2)-4·u(2,3)+u(2,4)+u(3,3)=0, u(2,3)+u(3,2)-4·u(3,3)+u(3,4)+u(4,3)=0 | u(3,3)+u(4,2)-4·u(4,3)+u(4,4)+u(5,3)=0, u(4,3)+u(5,2)-4·u(5,3)+u(5,4)=0, 0.294+u(1,3)-4·u(1,4)+u(1,5)+u(2,4) =0, u(1,4)+u(2,3)-4·u(2,4)+u(2,5)+u(3,4)=0, u(2,4)+u(3,3)-4·u(3,4)+u(3,5)+u(4,4)=0, u(3,4)+u(4,3)-4·u(4,4)+u(4,5)+u(5,4)=0, u(4,4)+u(5,3)-4·u(5,4)+u(5,5)=0, 0.154+u(1,4)-4·u(1,5)+u(2,5) =0, u(1,5)+u(2,4)-4·u(2,5)+u(3,5)=0, u(2,5)+u(3,4)-4·u(3,5)+u(4,5)=0, u(3,5)+u(4,4)-4·u(4,5)+u(5,5)=0, u(4,5)+u(5,4)-4·u(5,5)=0. |
Результат решения системы из 25 уравнений представлен в таблице:
| u(0,0) | 0.5 | 0.476 | 0.404 | 0.294 | 0.154 | 0 |
| 0.5 | 0.444618 | 0.389236 | 0.316975 | 0.225193 | 0.116966 | 0 |
| 0.476 | 0.389236 | 0.319355 | 0.249474 | 0.172833 | 0.0886772 | 0 |
| 0.404 | 0.316975 | 0.249474 | 0.188730 | 0.127986 | 0.0649079 | 0 |
| 0.294 | 0.225193 | 0.172833 | 0.127986 | 0.0854773 | 0.0429672 | 0 |
| 0.154 | 0.116966 | 0.0886772 | 0.0649079 | 0.0429672 | 0.0214836 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Следует отметить, что в трех точечном представлении конечно-разностные выражения производных второго порядка для внутренних и приграничных точек совпадают. Это позволяет для прямоугольных областей, заменив двумерную индексацию неизвестных ![]() одномерной
одномерной
![]() ,
,
преобразовать систему уравнений в векторно-матричную форму записи с блочно-диагональной матрицей коэффициентов, которая удобна для решения алгебраических уравнений с числом неизвестных более 100 на векторных вычислительных машинах:
![]() ,
,
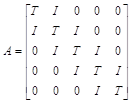 ,
, 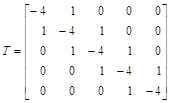 , I
, I
– матрицы, соответственно, блочная, коэффициентов и единичная;
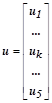 ,
, 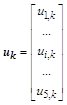 ,
, 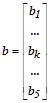 ,
,
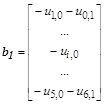 ,
, 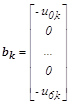 ,
, 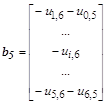
– соответственно, векторы неизвестных и правых частей уравнения со своими блочными компонентами.
В конечно-разностном представлении уравнения Лапласа каждое уравнение является для соответствующей точки области формулой вычисления среднего арифметического совокупности значений функции в соседних точках:
![]() .
.
Погрешность конечно-разностного представления уравнения Лапласа в виде системы алгебраических уравнений определяется погрешностью аппроксимации производных, которая для трех точечного варианта, приведенного выше, пропорциональна шагу сетки.
Естественно желание повысить точность аппроксимации лапласиана, добавив в структуру его конечно-разностного представления значения функции в дополнительных точках при сохранении суммирования значений из окружающих точек.
Похожие работы
... схема со сглаживанием, схема прямоугольник со сглаживанием, “шахматная ” схема. Произведены некоторые расчеты для одномерного уравнения переноса с переменными и постоянными коэффициентами на неравномерных сетках, с целью определения наиболее устойчивой разностной схемы. Исследование показало, что наиболее устойчивым методом для одномерного уравнения переноса с переменными коэффициентами является ...
... . Результаты моделирования можно просматривать на экране монитора и распечатывать на принтере. В данном расчетно-графическом задании виртуальная гибридная вычислительная машина будет использована в качестве вычислительного инструмента для решения краевых задач методами математического и аналогового моделирования, с целью демонстрации возможностей аналоговых устройств для исследования физических ...
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... суммы и позволит вычислить приближенное значение приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно ...






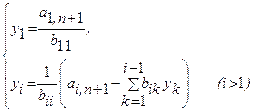
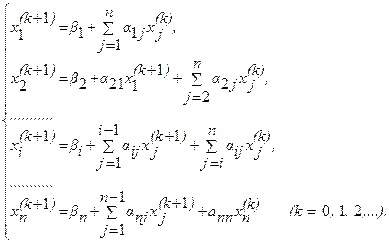
0 комментариев