Навигация
2. АЛГЕБРА МАТРИЦ
Рассмотрим действия над матрицами, но вначале введем несколько новых понятий.
Две матрицы А и В называются матрицами одного порядка, если они имеют одинаковое количество строк и одинаковое количество столбцов.
Пример. ![]() и
и ![]() – матрицы одного порядка 2´3;
– матрицы одного порядка 2´3;
![]() и
и ![]() – матрицы разных порядков, так как 2´3≠3´2.
– матрицы разных порядков, так как 2´3≠3´2.
Понятия ″больше″ и ″меньше″ для матриц не определяют.
Матрицы А и В называются равными, если они одного порядка m´n, и ![]() =
= ![]() , где
, где ![]() 1, 2, 3, …, m, а j = 1, 2, 3, …, n.
1, 2, 3, …, m, а j = 1, 2, 3, …, n.
Умножение матрицы на число.
Умножение матрицы А на число λ приводит к умножению каждого элемента матрицы на число λ:
λА = 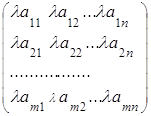 , λ
, λ![]() R.
R.
Из данного определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример.
Пусть матрица А =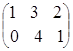 , тогда 5А=
, тогда 5А=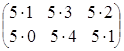 =
=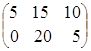 .
.
Пусть матрица В = 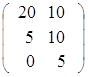 =
= 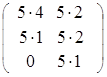 = 5
= 5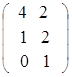 .
.
Свойства умножения матрицы на число:
1) λА = Аλ;
2) (λμ)А = λ(μА) = μ(λА), где λ,μ ![]() R;
R;
3) (λА)![]() = λА
= λА![]() ;
;
4) 0ּА = 0.
Сумма (разность) матриц.
Сумма (разность) определяется лишь для матриц одного порядка m´n.
Суммой (разностью) двух матриц А и В порядка m´n называется матрица С того же порядка, где ![]() =
= ![]() ±
± ![]() (
(![]() 1, 2, 3, …, m ,
1, 2, 3, …, m ,
j = 1, 2, 3, …, n.).
Иными словами, матрица С состоит из элементов, равных сумме (разности) соответствующих элементов матриц А и В.
Пример. Найти сумму и разность матриц А и В.
![]() =
= 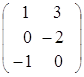 ,
, ![]() =
= 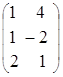 ,
,
тогда ![]() =
=![]() +
+![]() =
=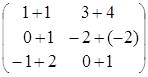 =
=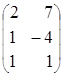 ,
,
![]() =
=![]() –
–![]() =
=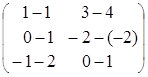 =
=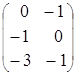 .
.
Если же ![]() =
= 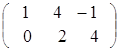 ,
, ![]() =
= 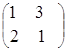 , то А ± В не существует, так как матрицы разного порядка.
, то А ± В не существует, так как матрицы разного порядка.
Из данных выше определений следуют свойства суммы матриц:
1) коммутативность А+В=В+А;
2) ассоциативность (А+В)+С=А+(В+С);
3) дистрибутивность к умножению на число λ![]() R: λ(А+В) = λА+λВ;
R: λ(А+В) = λА+λВ;
4) 0+А=А, где 0 – нулевая матрица;
5) А+(–А)=0, где (–А) – матрица, противоположная матрице А;
6) (А+В)![]() = А
= А![]() + В
+ В![]() .
.
Произведение матриц.
Операция произведения определяется не для всех матриц, а лишь для согласованных.
Матрицы А и В называются согласованными, если число столбцов матрицы А равно числу строк матрицы В. Так, еслиА=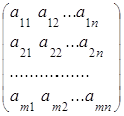 , В=
, В=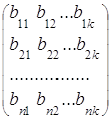
называется матрица С порядка m´k:
![]() =
=![]() ∙
∙![]() , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
![]() (
(![]() 1, 2, 3, …, m , j=1, 2, 3, …, k),
1, 2, 3, …, m , j=1, 2, 3, …, k),
то есть элемент ![]() i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.
i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.
Пример. Найти произведение матриц А и В.
![]() =
=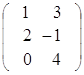 ,
, ![]() =
=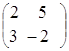 ,
,
![]() ∙
∙![]() =
=![]() =
=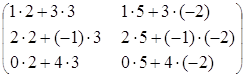 =
=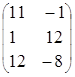 .
.
Произведение матриц В∙А не существует, так как матрицы В и А не согласованы: матрица В имеет порядок 2´2, а матрица А – порядок 3´2.
Рассмотрим свойства произведения матриц:
1) некоммутативность: АВ ≠ ВА, даже если А и В, и В и А согласованы. Если же АВ = ВА, то матрицы А и В называются коммутирующими (матрицы А и В в этом случае обязательно будут квадратными).
Пример 1. ![]() =
= ![]() ,
, ![]() =
= ![]() ;
;
![]()
![]() =
=![]() =
=![]() ;
;
![]()
![]() =
=![]() =
=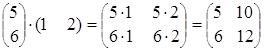 .
.
Очевидно, что ![]() ≠
≠ ![]() .
.
Пример 2. ![]() =
= 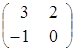 ,
, ![]() =
= 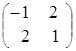 ;
;
![]()
![]() =
= ![]() =
= 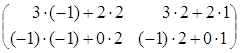 =
=![]()
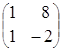 ;
;
![]()
![]() =
= ![]() =
= 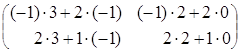 =
= 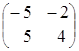 .
.
Вывод: ![]() ≠
≠![]() , хотя матрицы
, хотя матрицы ![]() и
и ![]() одного порядка.
одного порядка.
2) для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.
Пример.
![]() =
=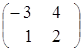 ,
, ![]() =
=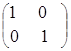 ;
;
![]()
![]() =
=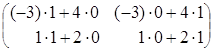 =
=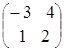 =
=![]() ;
;
![]()
![]() =
=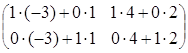 =
=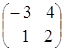 =
=![]() .
.
3) A·0 = 0·A = 0.
4) произведение двух матриц может равняться нулю, при этом матрицы А и В могут быть ненулевыми.
Пример.
![]() =
= 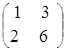 ,
, ![]() =
= 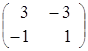 ;
;
![]()
![]() =
= 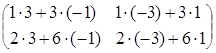 =
=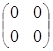 =
=![]() .
.
5) ассоциативность АВС=А(ВС)=(АВ)С:
![]() · (
· (![]() ·
·![]()
![]()
Пример.
Имеем матрицы 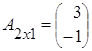 ,
, ![]() ,
, ![]()
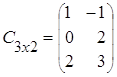 ;
;
тогда Аּ(ВּС) = ![]() (
(![]() ·
·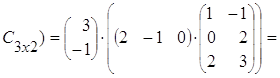
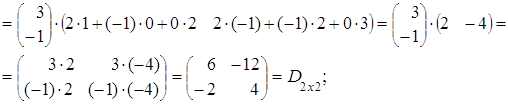
(АּВ)ּС=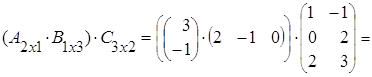
=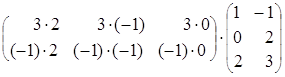 =
=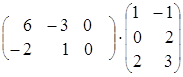 =
=
=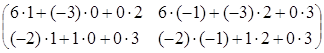 =
=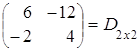 .
.
Таким образом, мы на примере показали, что Аּ(ВּС) = (АּВ)ּС.
6) дистрибутивность относительно сложения:
(А+В)∙С = АС + ВС, А∙(В + С)=АВ + АС.
7) (А∙В)![]() = В
= В![]() ∙А
∙А![]() .
.
Пример.
![]() =
=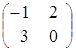 ,
, ![]() =
=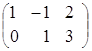 ,
,
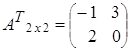 ,
, ![]() =
=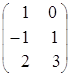 .
.
Тогда АВ=![]() ∙
∙![]() =
=![]()
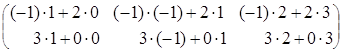 =
=
=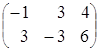
![]() (А∙В)
(А∙В)![]() =
= ![]() =
=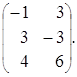
В![]() ∙А
∙А![]() =
=![]() ∙
∙![]() =
= 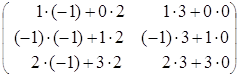 =
=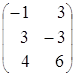 =
=![]() .
.
Таким образом, (А∙В)![]() = В
= В![]() А
А![]() .
.
8) λ(АּВ) = (λА)ּ В = Аּ (λВ), λ,![]() R.
R.
Рассмотрим типовые примеры на выполнение действий над матрицами, то есть требуется найти сумму, разность, произведение (если они существуют) двух матриц А и В.
Пример 1.
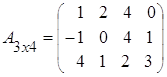 ,
, 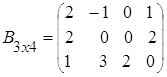 .
.
Решение.
1) ![]() +
+ ![]() =
= ![]() =
= 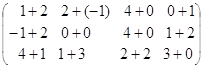 =
=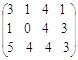 ;
;
2)![]() –
– ![]() =
=![]() =
=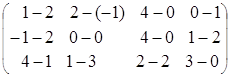 =
=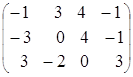 ;
;
3) произведение ![]()
![]() не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения
не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения ![]()
![]() по той же причине.
по той же причине.
Пример 2.
![]() =
=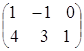 ,
, ![]() =
=![]() .
.
Решение.
1) суммы матриц, как и их разности, не существует, так как исходные матрицы разного порядка: матрица А имеет порядок 2´3, а матрица В – порядок 3´1;
2) так как матрицы А и В согласованны, то произведение матриц АּВ существует:
![]() ·
·![]() =
=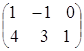 ·
·![]() =
=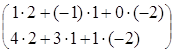 =
=![]() ,
,
произведение матриц ВּА не существует, так как матрицы ![]() и
и ![]() несогласованны.
несогласованны.
Пример 3.
![]() =
=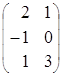 ,
, ![]() =
=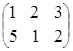 .
.
Решение.
1) суммы матриц, как и их разности, не существует, так как исходные матрицы разного порядка: матрица А имеет порядок 3´2, а матрица В – порядок 2´3;
2) произведение как матриц АּВ, так и ВּА, существует, так как матрицы согласованны, но результатом таких произведений будут матрицы разных порядков: ![]() ·
·![]() =
=![]() ,
, ![]() ·
·![]() =
=![]() .
.
![]() ·
·![]() =
=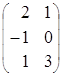 ·
·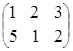 =
=
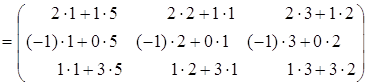 =
= 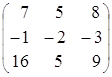 =
= ![]() ;
;
![]() ·
·![]() =
=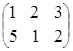 ·
·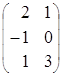 =
=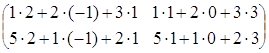 =
=
= 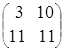 =
=![]()
![]() в данном случае АВ ≠ ВА.
в данном случае АВ ≠ ВА.
Пример 4.
![]() =
=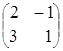 ,
, ![]() =
=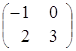 .
.
Решение.
1) ![]() +
+![]() =
=![]() =
=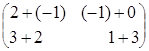 =
=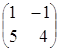 ,
,
2) ![]() –
–![]() =
= ![]() =
=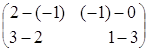 =
=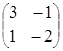 ;
;
3) произведение как матриц АּВ, так и ВּА, существует, так как матрицы согласованны:
![]() ·
·![]() =
=![]() =
=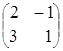 ·
·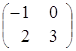 =
=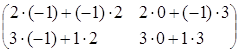 =
=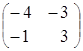 ;
;
![]() ·
·![]() =
=![]() =
=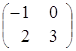 ·
·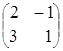 =
=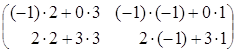 =
=
=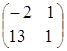
![]()
![]() ≠
≠![]() , то есть матрицы А и В некоммутирующие.
, то есть матрицы А и В некоммутирующие.
Пример 5.
![]() =
=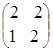 ,
, ![]() =
=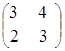 .
.
Решение.
1) ![]() +
+![]() =
=![]() =
=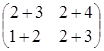 =
=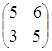 ,
,
2) ![]() –
–![]() =
=![]() =
=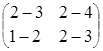 =
=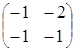 ;
;
3) произведение как матриц АּВ, так и ВּА, существует, так как матрицы согласованны:
![]() ·
·![]() =
=![]() =
=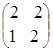 ·
·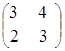 =
=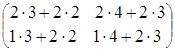 =
=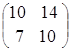 ;
;
![]() ·
·![]() =
=![]() =
=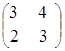 ·
·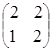 =
=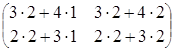 =
=
=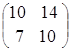
![]()
![]() =
=![]()
![]() АּВ=ВּА, т. е. данные матрицы коммутирующие.
АּВ=ВּА, т. е. данные матрицы коммутирующие.
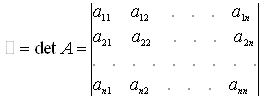
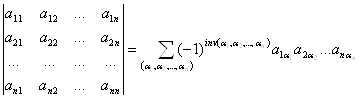
ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ
План
1. Определители квадратной матрицы и их свойства.
2. Теоремы Лапласа и аннулирования.
Ключевые понятия
Алгебраическое дополнение элемента определителя.
Минор элемента определителя.
Определитель второго порядка.
Определитель третьего порядка.
Определитель произвольного порядка.
Теорема Лапласа.
Теорема аннулирования.
Похожие работы
... элементов, стоящих на его главной и побочной диагоналях . Определитель третьего и любого другого порядка находится примерно также, а именно: Допустим, что у нас есть квадратная матрица . Определителем следующей матрицы является такое выражение : a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.. Как вы видите он просчитывается довольно легко, если запомнить определенную ...
... равен произведению определителй множителей. Это следует из Теоремы при Заключение В данной работе рассмотрена основная теория матриц и доказательство теоремы Коши-Бине. Также представлено применение данной теоремы при нахождении определителя произведения двух прямоугольных матриц в программе написанной на языке программирования Дельфи с возможностью ввода матриц вручную и подгрузкой из файла. ...
... генерируемой матрицы, то получившийся в результате разности размерностей массива и матрицы хвост перемножается с первыми элементами вспомогательного массива. 5. Организовать цикл для генерации матрицы, в которой получившийся массив в пункте 4 располагается на главной диагонали, и одна из областей, находящихся выше или ниже главной диагонали, заполняется случайными числами, принадлежащими ...
... получения количества обратимых матриц порядка n над полем Zp выглядит так: Данную формулу тождественными преобразованиями можно привести к виду: §3. Обратимые матрицы над кольцом Zn Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|. Для обратимых матриц A и B следует A·B=E.Следовательно |A·B|=|A|·|B|=|E|=1. Таким образом, ...






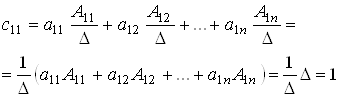

0 комментариев