Навигация
ОПРЕДЕЛИТЕЛИ КВАДРАТНОЙ МАТРИЦЫ И ИХ СВОЙСТВА
1. ОПРЕДЕЛИТЕЛИ КВАДРАТНОЙ МАТРИЦЫ И ИХ СВОЙСТВА
Пусть А – квадратная матрица порядка n:
А=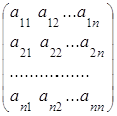 .
.
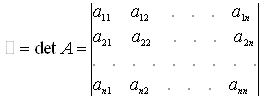
Каждой такой матрице можно поставить в соответствие единственное действительное число, называемое определителем (детерминантом) матрицы и обозначаемое
![]() = det A= Δ=
= det A= Δ=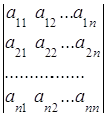 .
.
Отметим, что определитель существует только для квадратных матриц.
Рассмотрим правила вычисления определителей и их свойства для квадратных матриц второго и третьего порядка, которые будем называть для краткости определителями второго и третьего порядка соответственно.
Определителем второго порядка матрицы ![]() называется число, определяемое по правилу:
называется число, определяемое по правилу:
![]() =
=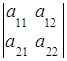 =
=![]()
![]()
![]() –
– ![]()
![]() , (1)
, (1)
т. е. определитель второго порядка есть число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Пример.
![]() =
=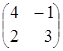 , тогда
, тогда ![]() =
=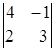 = 4 · 3 – ( –1) · 2=12 + 2 = 14.
= 4 · 3 – ( –1) · 2=12 + 2 = 14.
Следует помнить, что для обозначения матриц используют круглые или квадратные скобки, а для определителя – вертикальные линии. Матрица – это таблица чисел, а определитель – число.
Из определения определителя второго порядка следуют его свойства:
1. Определитель не изменится при замене всех его строк соответствующими столбцами:
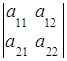 =
=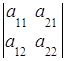 .
.
2. Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:
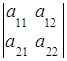 = –
= – 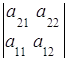 ,
, 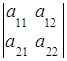 = –
= – 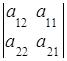 .
.
3. Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:
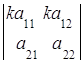 =
=![]()
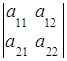 или
или 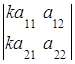 =
=![]()
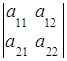 .
.
4. Если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю.
5. Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
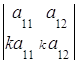 =0,
=0, 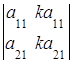 = 0.
= 0.
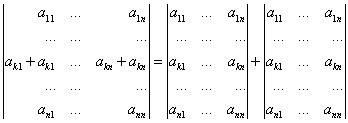
6. Если элементы одной строки (столбца) определителя равны сумме двух слагаемых, то такой определитель равен сумме двух определителей:
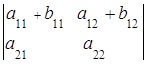 =
=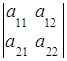 +
+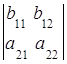 ,
, 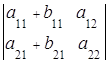 =
=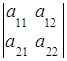 +
+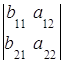 .
.
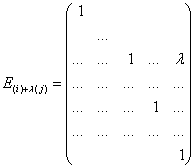
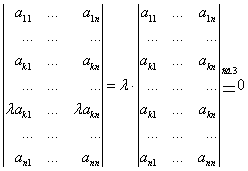
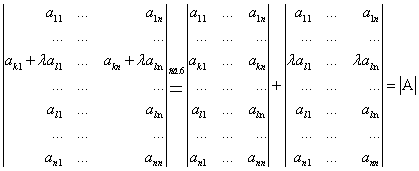
7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить (вычесть) соответственные элементы другой строки (столбца), умноженные на одно и тоже число ![]() :
:
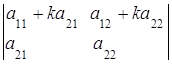 =
=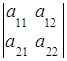 +
+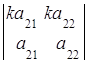 =
=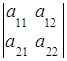 ,
,
так как 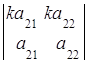 =0 по свойству 5.
=0 по свойству 5.
Остальные свойства определителей рассмотрим ниже.
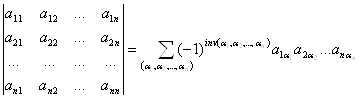
Введем понятие определителя третьего порядка: определителем третьего порядка квадратной матрицы называется число
Δ =![]() = det A=
= det A= 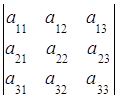 =
=
=![]()
![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
![]() –
– ![]()
![]()
![]() –
– ![]()
![]()
![]() –
– ![]()
![]()
![]() ,
,
(2)
т. е. каждое слагаемое в формуле (2) представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца. Чтобы запомнить, какие произведения в формуле (2) брать со знаком плюс, а какие со знаком минус, полезно знать правило треугольников (правило Саррюса):
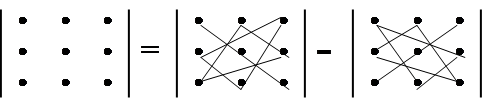
Пример. Вычислить определитель
![]() =
=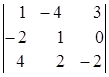 =
=
=![]() =
=
=![]() .
.
Следует отметить, что свойства определителя второго порядка, рассмотренные выше, без изменений переносятся на случай определителей любого порядка, в том числе и третьего.
Похожие работы
... элементов, стоящих на его главной и побочной диагоналях . Определитель третьего и любого другого порядка находится примерно также, а именно: Допустим, что у нас есть квадратная матрица . Определителем следующей матрицы является такое выражение : a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.. Как вы видите он просчитывается довольно легко, если запомнить определенную ...
... равен произведению определителй множителей. Это следует из Теоремы при Заключение В данной работе рассмотрена основная теория матриц и доказательство теоремы Коши-Бине. Также представлено применение данной теоремы при нахождении определителя произведения двух прямоугольных матриц в программе написанной на языке программирования Дельфи с возможностью ввода матриц вручную и подгрузкой из файла. ...
... генерируемой матрицы, то получившийся в результате разности размерностей массива и матрицы хвост перемножается с первыми элементами вспомогательного массива. 5. Организовать цикл для генерации матрицы, в которой получившийся массив в пункте 4 располагается на главной диагонали, и одна из областей, находящихся выше или ниже главной диагонали, заполняется случайными числами, принадлежащими ...
... получения количества обратимых матриц порядка n над полем Zp выглядит так: Данную формулу тождественными преобразованиями можно привести к виду: §3. Обратимые матрицы над кольцом Zn Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|. Для обратимых матриц A и B следует A·B=E.Следовательно |A·B|=|A|·|B|=|E|=1. Таким образом, ...







0 комментариев