Навигация
АЛГОРИТМ ПОСТРОЕНИЯ ОБРАТНОЙ МАТРИЦЫ
21463
знака
0
таблиц
16
изображений
2. АЛГОРИТМ ПОСТРОЕНИЯ ОБРАТНОЙ МАТРИЦЫ.
СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
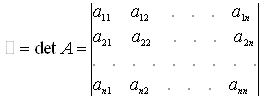
Покажем, что, если матрица А невырожденная, то для нее существует обратная матрица, и построим ее.
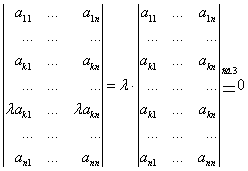
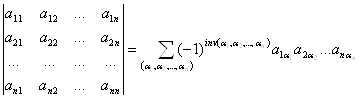
Пусть
А=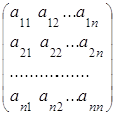
, 
.
Составим матрицу из алгебраических дополнений элементов матрицы А:
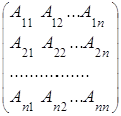
Транспонируя ее, получим так называемую присоединенную матрицу:
.
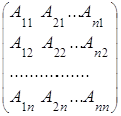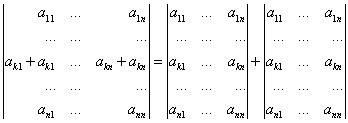
Найдем произведение 
ּ
. С учетом теоремы Лапласа и теоремы аннулирования:
ּ
= 
=
=
.
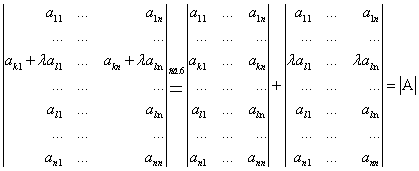
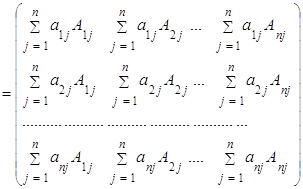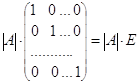
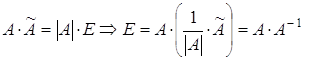Делаем вывод:
. (2)
Алгоритм построения обратной матрицы.
1)Вычислить определитель матрицы А. Если определитель равен нулю, то обратной матрицы не существует.
2)Если определитель матрицы не равен нулю, то составить из алгебраических дополнений соответствующих элементов матрицы А матрицу 
.
3)Транспонируя матрицу , получить присоединенную матрицу .
4)По формуле (2) составить обратную матрицу 
.
5)По формуле (1) проверить вычисления.
Пример. Найти обратную матрицу.
а). Пусть А=
. Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
б). Пусть А=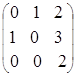
.
Вычислим определитель матрицы
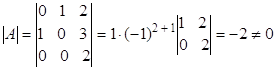
обратная матрица существует.
Составим матрицу из алгебраических дополнений
= 
= 
;
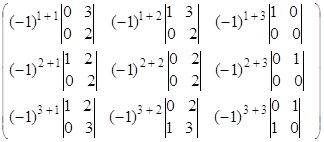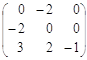транспонируя матрицу , получим присоединенную матрицу
;
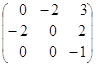по формуле (2) найдем обратную матрицу
=
=
.
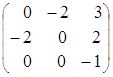Проверим правильность вычислений
=
= 
= 
.
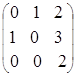
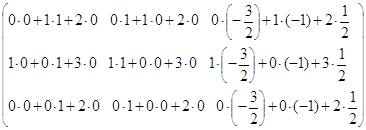Следовательно, обратная матрица построена верна.
Свойства обратной матрицы
1. 
;
2. 
;
3. 
.
4. ЗАДАЧИ И УПРАЖНЕНИЯ
Похожие работы
... элементов, стоящих на его главной и побочной диагоналях . Определитель третьего и любого другого порядка находится примерно также, а именно: Допустим, что у нас есть квадратная матрица . Определителем следующей матрицы является такое выражение : a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.. Как вы видите он просчитывается довольно легко, если запомнить определенную ...
... равен произведению определителй множителей. Это следует из Теоремы при Заключение В данной работе рассмотрена основная теория матриц и доказательство теоремы Коши-Бине. Также представлено применение данной теоремы при нахождении определителя произведения двух прямоугольных матриц в программе написанной на языке программирования Дельфи с возможностью ввода матриц вручную и подгрузкой из файла. ...
... генерируемой матрицы, то получившийся в результате разности размерностей массива и матрицы хвост перемножается с первыми элементами вспомогательного массива. 5. Организовать цикл для генерации матрицы, в которой получившийся массив в пункте 4 располагается на главной диагонали, и одна из областей, находящихся выше или ниже главной диагонали, заполняется случайными числами, принадлежащими ...
... получения количества обратимых матриц порядка n над полем Zp выглядит так: Данную формулу тождественными преобразованиями можно привести к виду: §3. Обратимые матрицы над кольцом Zn Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|. Для обратимых матриц A и B следует A·B=E.Следовательно |A·B|=|A|·|B|=|E|=1. Таким образом, ...
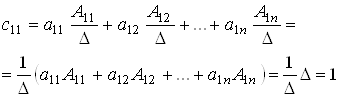
0 комментариев