Навигация
Матрицы и действия над ними
4.1 Матрицы и действия над ними
1. Найти сумму, разность, произведения двух матриц А и В.
а) 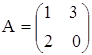 ,
,  ;
;
б)  ,
, 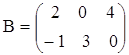 ;
;
в) 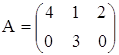 ,
, ![]()
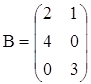 ;
;
г) 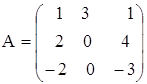 ,
, 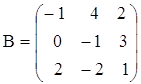 ;
;
д) ![]() ,
,  ;
;
е) 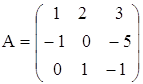 ,
, 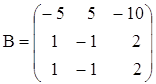 ;
;
ж) 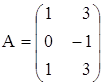 ,
, 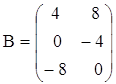 ;
;
з) 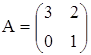 ,
,  ;
;
и) 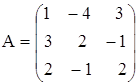 ,
, 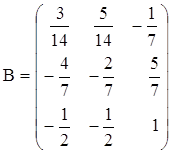 .
.
2. Доказать, что матрицы А и В коммутирующие.
а) 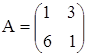 ,
, 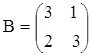 ; б)
; б) 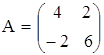 ,
, 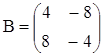 .
.
3. Даны матрицы А. В и С. Показать, что (АВ)·С=А·(ВС).
а) 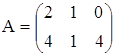 ,
, 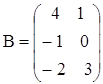 ,
, 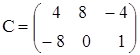 ;
;
б) ![]() ,
,  ,
, 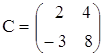 .
.
4. Вычислить (3А – 2В)·С, если
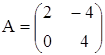 ,
, 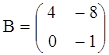 ,
, 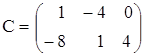 .
.
5. Найти ![]() , если
, если
а) 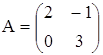 ; б)
; б)  .
.
6. Найти матрицу Х, если 3А+2Х=В, где
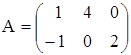 ,
, 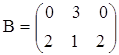 .
.
7. Найти АВС, если
а) 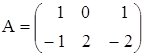 ,
, 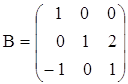 ,
, 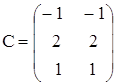 ;
;
б)  ,
, 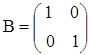 ,
, 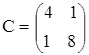 .
.
ОТВЕТЫ ПО ТЕМЕ «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ»
1. а) 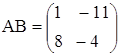 ,
, 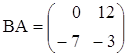 ;
;
б) произведения АВ и ВА не существуют;
в) 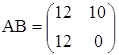 ,
,  ;
;
г)  ,
,  ;
;
д) суммы, разности и произведения ВА матриц не существуют, ![]() ;
;
е) ![]() ,
,  ;
;
ж) произведения матриц не существуют;
з) 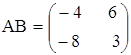 ,
,  ;
;
и) 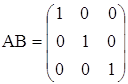 ,
, 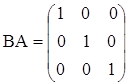 .
.
2. а) 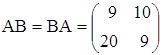 ; б)
; б) 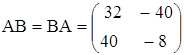 .
.
3. а) 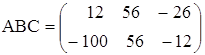 ; б)
; б) ![]() .
.
4. 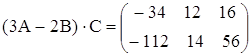 .
.
5. а) 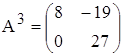 ; б)
; б)  .
.
6. 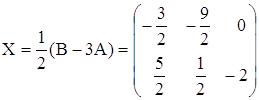 .
.
7. а) 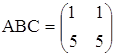 ; б)
; б)  .
.
1. Вычислить определители
2.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
ж)  ; з)
; з) 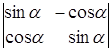 .
.
3. С помощью правила треугольников вычислить определители
а)  ; б)
; б)  ; в)
; в) 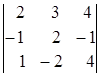 ; г)
; г) 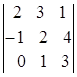 .
.
4. Вычислить определители примера 2, используя теорему Лапласа.
5. Вычислить определители, предварительно упростив их:
а) 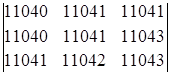 ; б)
; б) 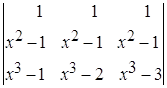 ; в)
; в) 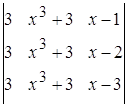 ;
;
г) 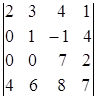 ; д)
; д) 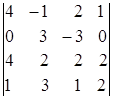 ; е)
; е)  ;
;
ж) 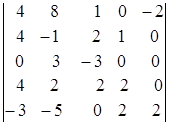 .
.
6. Вычислить определитель методом приведения его к треугольному виду
 .
.
7. Пусть даны матрицы А и В. Доказать, что ![]() :
:
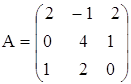 ,
, 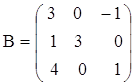 .
.
ОТВЕТЫ ПО ТЕМЕ «ОПРЕДЕЛИТЕЛИ»
1. а) 10; б) 1; в) 25; г) 16; д) 0; е) –3; ж) -6; з) 1.
2. а) –25; б) 168; в) 21; г) 12.
3. а) –25; б) 168; в) 21; г) 12.
4. а) 2; б) 0; в) 0; г) 70; д) 18; е) –66; ж) -36.
5. –24.
4.3 Обратная матрица1. Найти обратную матрицу:
а) ![]() ; б)
; б) 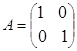 ; в)
; в) 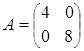 ; г)
; г) 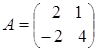 ;
;
д)  ; е)
; е) 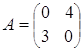 ; ж)
; ж) 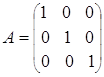 ; з)
; з)  ;
;
и) 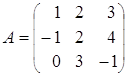 ; к)
; к) 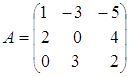 ; л)
; л) 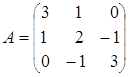 ;
;
м) 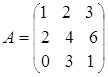 ; н)
; н) 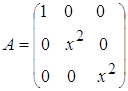 .
.
2. Найти обратную матрицу и проверить выполнение условия ![]() :
:
а)  ; б)
; б) 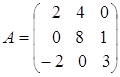 .
.
3. Доказать равенство ![]() :
:
а) 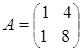 ,
, 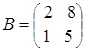 ; б)
; б)  ,
,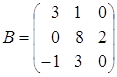 .
.
4. Доказать равенство ![]() :
:
а) 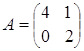 ; б)
; б)  .
.
1. а)  ; б)
; б) ![]()
![]() ; в)
; в)  ; г)
; г) 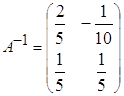 ;
;
д)  ; е)
; е) 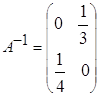 ; ж)
; ж) ![]()
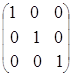 ;
;
з) 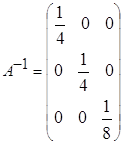 ; и)
; и) 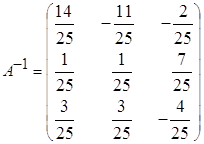 ;
;
к) 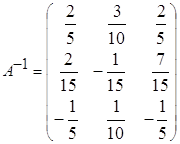 ; л)
; л) 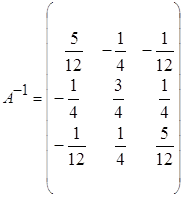 ;
;
м) ![]() ; н)
; н) 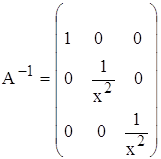 .
.
2. а) 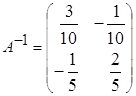 ; б)
; б) 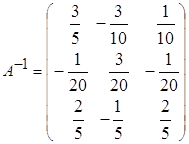 .
.
2. а) 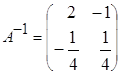 ,
, 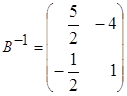 ,
, ![]() =
= ;
;
б) 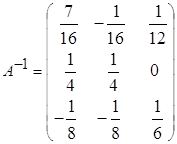 ,
, 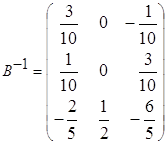 ,
,
![]() =
=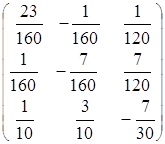 .
.
5. а) 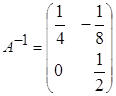 ,
,  ,
,
 ,
, 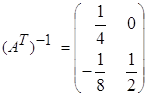 ;
;
б) 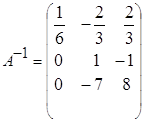 ,
, 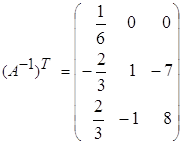 ,
,
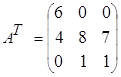 ,
, ![]()
 .
.
5. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. Вычислить определитель разложением
а) по i- той строке;
б) по j- тому столбцу.
1.1. 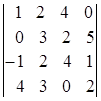 ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ;
;
i=2, j=3. i=4, j=1. i=3, j=2.
1.4. 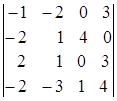 ; 1.5.
; 1.5. 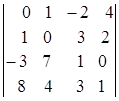 ; 1.6.
; 1.6. 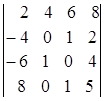 ;
;
i=3, j=3. i=1, j=4. i=2, j=2.
1.7. 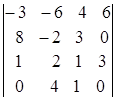 ; 1.8.
; 1.8. 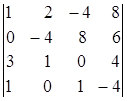 ; 1.9.
; 1.9.  ;
;
i=4, j=4. i=2, j=2. i=3, j=2.
1.10.  ; 1.11.
; 1.11. 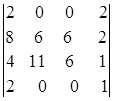 ; 1.12.
; 1.12.  ;
;
i=2, j=1. i=1, j=2. i=3, j=2.
1.13. 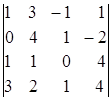 ; 1.14.
; 1.14. 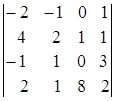 ; 1.15.
; 1.15. 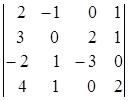 ;
;
i=2, j=3. i=1, j=3. i=4, j=2.
1.16.  ; 1.17.
; 1.17. 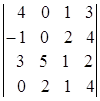 ; 1.18.
; 1.18. 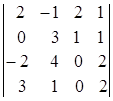 ;
;
i=2, j=3. i=2, j=4. i=1, j=3.
1.19.  ; 1.20.
; 1.20. 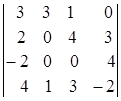 ; 1.21.
; 1.21. 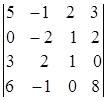 ;
;
i=2, j=2. i=1, j=4. i=3, j=2.
1.22. 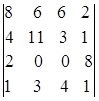 ; 1.23.
; 1.23. 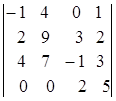 ; 1.24.
; 1.24.  ;
;
i=1, j=3. i=2, j=1. i=3, j=4.
1.25. 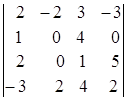 ; 1.26.
; 1.26. 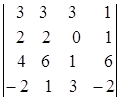 ; 1.27.
; 1.27.  ;
;
i=4, j=3. i=3, j=3. i=1, j=2.
1.28. 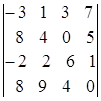 ; 1.29.
; 1.29. 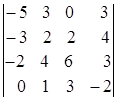 ; 1.30.
; 1.30. 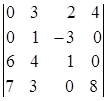 .
.
i=3, j=3. i=2, j=1. i=3, j=2.
ЛИТЕРАТУРА
1. Жевняк Р.М., Карпук А.А. Высшая математика. – Мн.: Выш. шк., 1992.- 384 с.
2. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Мн.: Тетрасистемс, 1998.- 288 с.
3. Марков Л.Н., Размыслович Г.П. Высшая математика. Часть 1. –Мн.: Амалфея, 1999. – 208 с.
4. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. I семестр. М.: Новое знание, 2002.- 140 с.
5.Коваленко Н.С., Минченков Ю.В., Овсеец М.И. Высшая математика. Учеб. пособие. -Мн.: ЧИУП, 2003. – 32 с.
Похожие работы
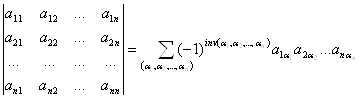
... элементов, стоящих на его главной и побочной диагоналях . Определитель третьего и любого другого порядка находится примерно также, а именно: Допустим, что у нас есть квадратная матрица . Определителем следующей матрицы является такое выражение : a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.. Как вы видите он просчитывается довольно легко, если запомнить определенную ...
... равен произведению определителй множителей. Это следует из Теоремы при Заключение В данной работе рассмотрена основная теория матриц и доказательство теоремы Коши-Бине. Также представлено применение данной теоремы при нахождении определителя произведения двух прямоугольных матриц в программе написанной на языке программирования Дельфи с возможностью ввода матриц вручную и подгрузкой из файла. ...
... генерируемой матрицы, то получившийся в результате разности размерностей массива и матрицы хвост перемножается с первыми элементами вспомогательного массива. 5. Организовать цикл для генерации матрицы, в которой получившийся массив в пункте 4 располагается на главной диагонали, и одна из областей, находящихся выше или ниже главной диагонали, заполняется случайными числами, принадлежащими ...
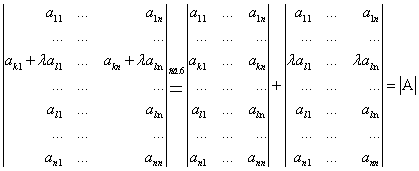
... получения количества обратимых матриц порядка n над полем Zp выглядит так: Данную формулу тождественными преобразованиями можно привести к виду: §3. Обратимые матрицы над кольцом Zn Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|. Для обратимых матриц A и B следует A·B=E.Следовательно |A·B|=|A|·|B|=|E|=1. Таким образом, ...
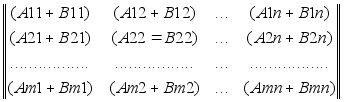
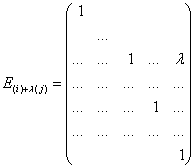

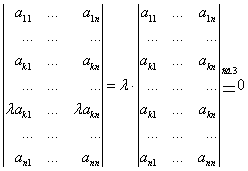
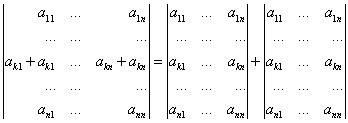






0 комментариев