Скалярний добуток векторів

6. Скалярний добуток векторів

 

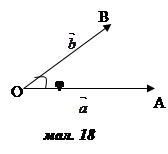
Нехай ,  − ненульові вектори. Відкладемо від деякої точки O вектори =, =. Кутом між векторами  і  називається кут між променями OA і OB (мал. 18). Позначають: (,) = φ. Для будь-яких векторів  і  маємо 0 ≤ (,) ≤ π.

Означення: скалярним добутком двох векторів називається число, яке дорівнює добутку їх довжин на косинус кута між ними:   =cos(,).

Теорема: скалярний добуток векторів (, , ), (, , ), заданих в ортонормованому базисі, обчислюються за формулою:

 =  +  + . /6/

 

Доведення. Якщо один із векторів або обидва нульові, то формула очевидна. Припустимо, що ,  і розглянемо два випадки.

1. Вектори  і  не колінеарні. Відкладемо вектори  = ,  = (мал. 19). Нехай (, ) = φ.

З OAB за теоремою косинусів  – 2 OAOBcosφ, або ,

звідки

=. Отже,  =  + + .

2. Вектори  і  колінеарні. Тоді  = λ,  = λ,  = λ,  = λ;

= λ = cos(λ, ) = λ= λ() = λ + λ + λ =  +  +

Теорему доведено.

З теореми і означення випливають такі властивості скалярного добутку векторів:

1. = 0 тоді і тільки тоді, коли , якщо , .

2. = = = .

3.  = .

4. (α )  = α(),α  R;

5. ( + ) =   +  .

Формула, аналогічна до формули /6/, має місце і в просторі . Справді, нехай в ортонормованому базисі простору  задано вектори (, ), (, ). Тоді, користуючись властивостями 1–5, дістанемо:  = ( + )( + )=    + ( + ) +  =  + . Отже,  =  +  /7/

З означення скалярного добутку і /6/, /7/ випливають такі формули для обчислення косинуса кута між векторами:

– у просторі :

cos(, ) = ;

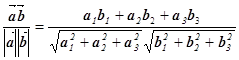– в просторі :

cos(, ) = .

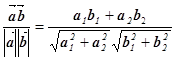Векторна алгебра може ефективно використовуватися для розв’язування задач елементарної геометрії.

Практична частина

 

Задача 1. Довести, що коли точка D ділить відрізок AB у відношеннях m: n, а C – довільна точка площини, то  /*/.

 

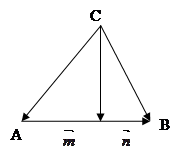
Доведення: Введемо позначення:

AD: DB = m: n;  = ;  = .

 ||  = , але  =  – ,

 =  – , тому  –  =  – .

Звідси (1 + ) =  + , і остаточно  =  + , що і треба було довести.

Задача 2. Якщо точки M і N належать відрізкам AB і CD, та AM: MB = CN: ND = m: n, то виконується рівність  =  + .

Доведення: за умовою та за формулою, що була доведена в задачі 1, маємо: =+=(+)+(+)=  +  +(m+n). Вираз m+n= , отже ми довели, що і треба було довести.

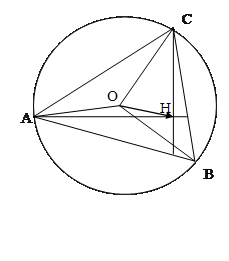Задача 3. У трикутнику ABC точка O – центр описаного кола, H – точка перетину його висот. Довести, що .

Доведення: за умовою  (за означенням скалярного добутку). Проте, , , тому ()()=0 /1/. Крім того, ()()=0 /2/ (як радіуси описаного кола). Віднімаючи /2/ від /1/, матимемо ()( – ) = 0. Аналогічно з умов = 0 і , маємо ()( – ) = 0. Оскільки  і , то вектор, перпендикулярний до кожного з них, може бути тільки нульовим, тобто  – = 0. Звідси , що і треба було довести.

Задача 4. В коло вписано чотирикутник ABCD, перетинаються в точці M. Через середину S сторони CD проведено пряму SM так, що (AB) (SM) = K. Довести, що AK: KB = : .

Доведення: позначимо AK: KB = x. Тоді за формулою /*/ (див. задачу 1) . Оскільки вектори  і  колінеарні, а точка S є серединою відрізка CD, то . Використавши рівність MA MC = MBMD = k дістанемо . Отже, , а

 . За теоремою про єдність розкладу вектора за двома не колінеарними векторами маємо

Звідси x = .

Задача 5. Дано три точки A, B, C і деяка точка O. Довести, що рівність  /#/ при AB є необхідною і достатньою умовою належності точок A, B, C одній прямій.

Доведення: Необхідність. Нехай точки A, B, C належать одній прямій, тоді . Ця рівність рівносильна такій .Звідси .

Достатність. Нехай . Тоді  або , тому  і  колінеарні, і, отже, A, B, C належать одній прямій.

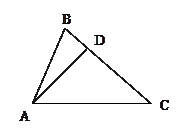Задача 6. Точка D належить стороні BC трикутника ABC. Довести, що .

Доведення: за формулою /#/ маємо . Оскільки

. Отже, , що і треба було довести.

Задача 7. Довести, що косинус кута між медіанами катетів рівнобедреного трикутника дорівнює .

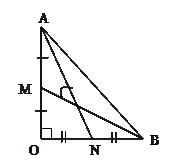Доведення: нехай задано рівнобедрений прямокутний трикутник OAB (OA = OB = a), точки M і N – відповідно середини OA і OB. Розмістимо цей трикутник в прямокутну систему координат так, щоб точка O збігалася з початком координат, а катети OA і OB лежали на відповідних осях координат x і y. Тоді в цій системі координат матимемо A (a; 0), B (0; a), M(; 0), N (0;). Вектори, які збігаються з медіанами, матимуть координати (-a; ) і (; a). Кут між медіанами – це кут між векторами  і , який знайдемо за формулою: cos(,)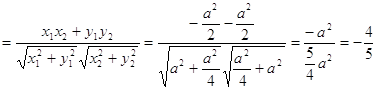, що й треба було довести.

Задача 8. Довести, що медіани трикутника перетинаються в одній точці і діляться нею у відношенні 2: 1, рухаючи від вершин.

Доведення: нехай , ,  – медіани трикутника ABC;  і  перетинаються в точці O. Тоді  (бo || ) і  (бо ||). Звідси - = . Враховуючи єдність розкладу вектора за двома неколінеарними векторами  і , знаходимо, що k = -1, – p = 1. Отже, , то . За умовою , тому , або OC:  = 2: 1 і, отже, точки C, O,  належать одній прямій. З цього випливає, що медіана  також проходить через точку О і ділиться нею у відношенні 2: 1, рахуючи від вершини, що й треба було довести.

Задача 9. Дано правильну чотирикутну піраміду SABCD. Чи є лінійно залежними вектори: а)  і ; б)  і ; в) ; г) ; д) ; е) ?

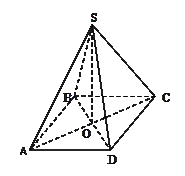Розв’язання: вектори  і  неколінеарні, тому за теоремою про колінеарні вектори вони не є лінійно залежними.

 і  колінеарні, а тому лінійно залежні.

і  колінеарні, отже, лінійно залежні; за властивістю три вектори  також лінійно залежні.

Вектори  компланарні, тому за теоремою вони лінійно залежні.

 не є компланарними, за теоремою вони не є лінійно залежними.

 – три некомпланарні вектори. За теоремою про розклад вектора за трьома не компланарними векторами, вектор  є лінійною комбінацією цих векторів. За властивістю  лінійно залежні.

Задача 10. Обчислити кут між векторами  і , де  і  – одиничні взаємно перпендикулярні вектори.

Розв’язання: формула косинуса кута: cos(,)=. Обчислимо ,,.

;

.

Тоді cos(,) = ; cos(,) = .

Відповідь: .

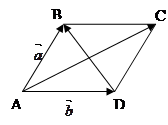Задача 11. Довести, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів всіх його сторін.

Розв’язання: Нехай ABCD – даний паралелограм. Покладемо , (). За означенням суми і різниці векторів . Використовуючи властивості скалярного квадрату, отримаємо:  тобто .

Задача 12. З якою силою F треба утримувати вантаж вагою P на похилій площині, щоб він не скочувався вниз?

Розв’язання: нехай O – центр маси вантажу, до якого прикладено силу P. Розкладемо вектор  за двома взаємно перпендикулярними напрямами, як показано на малюнку. Сила  перпендикулярна до похилої площини і не викликає переміщення вантажу. Сила F, яка утримує вантаж, має дорівнювати за величиною і бути протилежною за напрямом силі OB. Тому F = P sinα.

 

Висновок

Таким чином в своїй курсовій роботі на тему «Метод векторів та його застосування» я подала короткі теоретичні відомості про поняття вектора, рівносильність векторів, додавання, віднімання та множення вектора на число, колінеарність, компланарність, лінійну залежність векторів, координати вектора, скалярний добуток векторів а також про векторний простір та його підпростори. А в практичній частині, на прикладах показала доцільність його застосування. Метод векторів широко застосовується в різних галузях науки (математиці, фізиці). Часто його застосування значно полегшує розв’язування деяких задач, а інших випадках задачу взагалі неможливо розв’язати іншим способом.

Література

1. Базылев В.Т., Дуничев К.И., Иваницкая В.П. Геометрия, Ч.І. – М: Просвещение, 1974. – 351 с.

2. Атанасян Л.С., Базылев В.Т. Геометрия, Ч.І – М: Просвещение, 1986. – 336 с.

3. Атанасян Л.С. Геометрия, Ч.І – М: Просвещение, 1967. – 300 с.

4. Атанасян Л.С., Атанасян В.А. Сборник задач по геометри, Ч.І. – М: Просвещение, 1973. – 256 с.

5. Яковець, Боровик, Коваленко. Аналітична геометрія: навч. пос. – Суми: Університецька книга, 2004. – 295 с.

6. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии, М: Наука, 1970. – 335 с.

7. Клетенник Д.В. Сборник задач по аналитической геометри, М: Наука, 1972. – 240 с.

8. Панішева О.В. Векторний метод: Інтегрований урок геометрії та фізики, Математика. – 2000. – №14. – с. 4 – 5.

9. Єгорова Г.О. Векторний і координатний методи розв’язування задач, Математика. – 2001. – №5. – с. 5 – 11.