Непозиционные и позиционные системы счисления
Докажем существование представления любого натурального числа в виде
Системы счисления с другими основаниями, их происхождение и применение
Умножение и деление
Перевод чисел из одной системы счисления в другую
ИСПОЛЬЗОВАНИЕ СИСТЕМ СЧИСЛЕНИЯ В КОМПЬЮТЕРНОЙ ТЕХНИКЕ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЯХ
Способы построения двоичных кодов
Навигация
Докажем существование представления любого натурального числа в виде
Системы счисления и основы двоичных кодировок
54749
знаков
16
таблиц
10
изображений
1. Докажем существование представления любого натурального числа в виде
N=anρn+a n-1 ρn-1 + ... +аρ+а0 (1)
Доказательство проведем методом полной математической индукции.
Представление числа N в виде (1) возможно для первых р-1 натуральных чисел 1, 2,..., ρ-1, так как n=1 и число совпадает с данным числом. Представление числа в виде (1) для чисел 1, 2, . . . ,ρ-1, очевидно, возможны только единственным способом: 1=1, 2=2,. . . ,ρ-1=ρ-1.
Предположим, что все натуральные числа N≤k (к≥1) представимы в виде (1). Докажем что число к+1 так же представимо в виде (1). Для этого разделим с остатком число к+1 на ρ:
K+l=sρ+r, 0<г<ρ-1 (2)
где s - неполное частное и г - остаток.
Так как число s≤k, то оно по предположению индукции представимо в виде (1):
s = аnρn+ . . . +a1ρ +а0 (3)
где 1≤аn≤ρ -1, 0≤ ai≤ρ -l, (i=0,1,..,n-1)
Подставим выражения (2) и (3), получим:
k+l= (anρ+ ... +аiρ +а0) ρ + г = аnρ +... + aiρ +a0ρ +г (4)
где 1 ≤ an ≤ρ -1, 0≤ aj ≤ ρ -1, 0 ≤ г ≤ ρ -1 0=0,1,. . ,n-1)
Это выражение (4) дает представление числа к+1 в виде (1):
К+1=b n+1ρ n+1 + bn ρ n + ... + b1ρ +b0
где b0 =r, bi+1- ai (i=0,l,.. ,n-l)
2. Докажем единственность представления любого натурального числа в виде (1).
Доказательство проведем методом математической индукции.
Для чисел 1, 2,... , ρ -1 представление в виде (1) единственно.
Предположим что для всех натуральных N≤k (к≥1) представление в виде (1) единственно. Докажем, что число к+1 может быть представлено в виде (1) только одним способом. Для этого разделим с остатком число к+1 на ρ:
K+l=sρ+r, 0<г< ρ -1 (5)
Предположим, что к+1 имеет два различных способа представления:
к+1=а nρ n + аn-1 ρ n-1 + ....+ а1ρ +а() (6)
к+1 =b mρ m + bm-1 ρ m-1 + ... + b1ρ +b0 (7)
Представим: равенства (6) и (7) в виде:
k+1= (а nρ n-1 + an-1 ρ n-2+ ... + а1)ρ+а0 (6*)
k+1 = (b mρ m-1 + bm-1 ρ m-2+ ... + b)ρ+b0 (7*)
Так как 0 ≤ а0 ≤ρ -1 и 0 ≤ b0 ≤ρ -1, то из (6*) и (7*) следует, что неполное частное s и остаток г в формуле (5) будут:
S= аnρ n-1 + аn-1 ρ n-2 + ... + a1=bmρ m-1 + bm-1 ρ m-2+ ... + b1. r = a0 = b0
Так как s ≤ k, из индуктивного предположения следует, что число s имеет единственно представление в виде (1), то есть
n-l = m-l, ai =bi , (i=0,1, . . ,n-1).
Из последнего равенства имеем а0=bо. Таким образом, n=m, ai=bi (i=0,l, . . ,n-l), но это противоречит допущению, что число k+1. имеет два различных представления (6) и (7). Следовательно, число к+1 представляется в виде (1) единственным образом. На основании принципа математической индукции утверждение справедливо для любого N . Теорема доказана.
1.3 Десятичная система счисления, ее происхождение и применение.
Представьте, что вы пересчитываете большое число одинаковых предметов, например, спичек. Удобнее всего будет разложить эти предметы как кучки по десять в каждой. Получится некоторое количество десятков (и, может быть, останутся несколько предметов, не вошедших в целые десятки). Далее придется пересчитывать кучки (десятки). Если кучек (десятков) будет очень много, можно их тоже сгруппировать в десятки, и так далее.
Таким путем мы приходим к основной идее нашей системы счисления — к мысли о единицах различных разрядов. Десять единиц образуют один десяток, то есть десять единиц первого разряда образуют одну единицу второго разряда, десять единиц второго - единицу третьего и так далее.
Несмотря на свою кажущуюся простоту, такая система счисления прошла очень долгий путь исторического развития. В ее создании принимали участие многие народы.
Возникает вопрос - почему стали раскладывать предметы на десятки, а не на пятки или дюжины? Почему единицы каждого разряда в десять, а не в восемь или три раза больше единиц предыдущего разряда?
Счет десятками получил широкое распространение потому, что люди располагают естественной "счетной машиной", связанной с числом десять -десятью пальцами на руках.
Десятичная нумерация "изобретена" индусами; в Европу ее занесли арабы, вторгшиеся в Испанию в VIII в. нашей эры. Арабская нумерация распространилась по всей Европе, и, будучи проще и удобнее остальных систем счисления, быстро их вытеснила. До сих пор наши цифры принято называть арабскими. Впрочем, за тысячу лет все цифры, кроме 1 и 9, сильно изменились. Вот, для сравнения, наши (называемые арабскими) и настоящие арабские цифры:
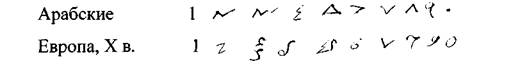
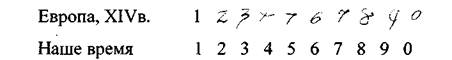
Названия первых шести разрядов (единицы, десятки, сотни, тысячи и так далее) очень древние и у разных народов звучат по-разному.
Слово "миллион" сравнительно недавнего происхождения. Придумал его известный венецианский путешественник Марко Поло, которому не хватало обыкновенных чисел, чтобы рассказать о необычайном изобилии людей и богатств далекой Небесной Империи (Китай). По-русски слову "миллион" могло бы соответствовать несуществующее слово "тысячища".
Для построения числовых наименований более высоких порядков используются латинские числительные (биллионы, триллионы). Построенные таким образом названия мало удобны, латынь знают не все. Да и вообще такие числа встречаются только в сборниках математических курьезов, да в некоторых отделах теории чисел. Нет необходимости придумывать им рациональные названия. Здесь на помощь приходит понятие степени. Число, изображаемое единицей с нулями, является степенью десятки: 100= 102, 1000= 103, 10...00...00= 10n.
Эти соображения позволяют нам очень коротко и удобно записывать все числа, которые даются нам наукой и жизнью. Например, масса Земного шара - 6 000 000 000 000 000 000 000 тонн. Мы можем записать: 6 • 1021 тонн, и назвать "шесть на десять в двадцать первой степени", это коротко и удобно.
В практической жизни при счете предметов, которых очень много, например, жителей страны, при измерении различных величин, удается определить только первые несколько цифр результата. Любое число, данное практически, удается записать как произведение не более чем восьмизначного (чаще трех - четырехзначного) числа на "единицу с нулями". Например, поверхность Земли - 509 000 000 км2. Можно записать так: 509 • 106км2.
Классическим примером числового гиганта является награда, которую, если верить старинной легенде, потребовал себе изобретатель шахматной доски: за первую клетку доски — одно зерно риса, за вторую — два, за третью - четыре и так далее, за каждую последующую - в два раза больше, чем за предыдущую. Эта скромная на вид просьба оказалась невыполнимой: все житницы мира не смогут вместить риса, затребованного хитрым изобретателем.
Таким образом, для обозначения и записи чисел мы пользуемся позиционной десятичной нумерацией. Позиционной она называется потому, что значение цифры зависит от ее положения - места в ряду других цифр в записи числа; десятичной - потому, что из двух написанных рядом цифр левая обозначает единицы в десять раз большие, чем правая. Для обозначения и записи чисел в пределах миллиарда эта система очень удобна. При записи очень больших чисел пользуются понятием степени числа.
Похожие работы
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... . В случае выбора пункта «выход», необходимо реализовать завершение работы программы и передачу управления операционной системе DOS. 1.3. Требования техническим и программным средствам Программа выполнена на языке ассемблера 8086 процессора, соответственно ей необходим IBM PC – совместимый компьютер с процессором не ниже 8086, также программа может выполняться на компьютерах с ...
... в широкую практику разработки программ объектно-ориентированного программирования, впитавшего в себя идеи структурного и модульного программирования, структурное программирование стало фактом истории информатики. Билет № 9 Текстовый редактор, назначение и основные функции. Для работы с текстами на компьютере используются программные средства, называемые текстовыми редакторами или текстовыми ...
... можно изобразить отдельно. Формирователь выхода «Равенство кодов» Формирователь выхода «Больше» Формирователь выхода «Меньше». Арифметические устройства Другой класс приборов, используемых в дискретной технике предназначен для выполнения арифметических действий с двоичными числами: сложения, вычитания, умножения, деления. К арифметическим устройствам относятся также схемы, ...
0 комментариев